Correlation is what you are doing when you compare two sets of measurements (each set is called a variable).  If you were to measure everyone’s height and weight, you could then compare heights and weights and see if they have any relationship to each other -- any "co-relation," if you will.  Of course, the taller you are, generally speaking, the more you weight.  But it is obviously not a perfect co-relation, because some people are thin and some are fat.

A perfect correlation is +1.  Very close to perfect would be a comparison of men's shoe size and their... foot length.  For example, here is some data:

	Shoe size	Foot length (inches)
John	4 1/2	9 1/4
Dave	5	9 3/8
Sam	5	9 1/4
Jim	6 1/2	9 1/2
Ed	6 1/2	9 3/4
Bob	7	9 3/4
Ted	8	10 1/8
Matt	11 1/2	11
Damian	12	11 1/4
Horton	14	11 3/8

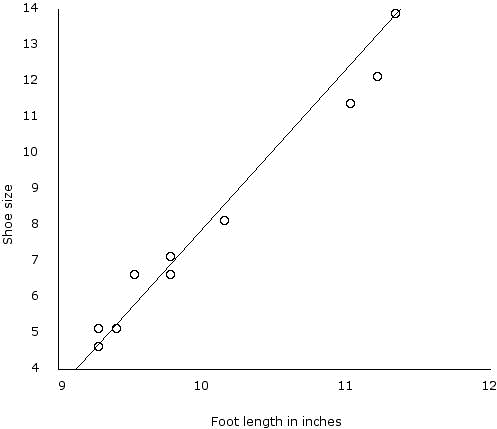
This is called a scatter plot.  The line is the line that describes the "best fit" -- in other words, it accounts for the data most nicely.  This one is not perfect -- apparently, some guys buy shoes that are too tight, and some buy shoes that are too loose!  But you can see by comparing the dots to the line, it's pretty close to a +1 correlation.

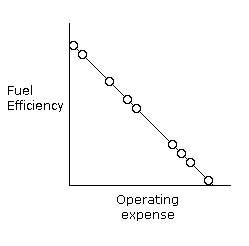
Perfect correlation can also be -1.  An example would be your car's fuel efficiency and how much money you need to spend for gas per so many miles.  It should look like this:

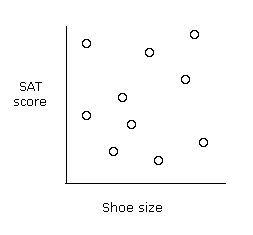
Most things have a correlation of 0 (or close to it).  An example would be your shoe size vs your... SAT score.

For a more real life example of data, along with a scatter plot and an actual correlation, is this one, which compares homicide rates with hand gun ownership.  (The figures are real for the late 1980's.)

Here's the scatter plot:

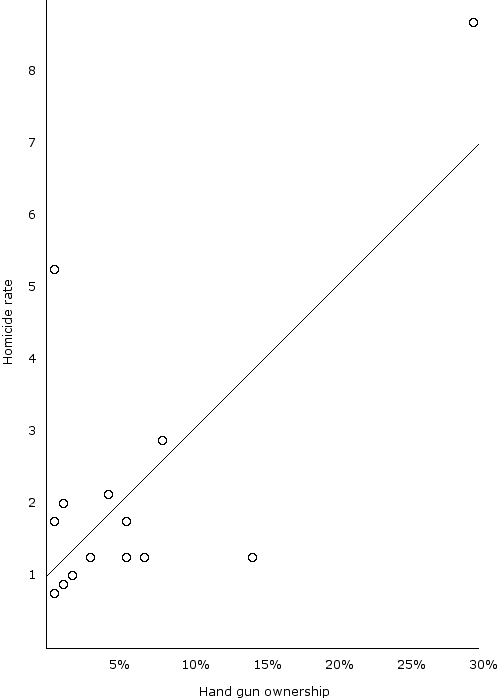
And the correlation:  +.70.  That is quite impressive, and maybe it says something about the various societies.  If you are wondering about Switzerland's figures, it should be noted that every adult male is trained in the army and is required to maintain weapons in his home -- just in case they get invaded by, say, Italy.  On the other hand, you can see that Northern Ireland has a high homicide rate even though few people own guns.  I think you can guess why!

If you would like a more meaningful number than correlation itself, you can square it.  This will give you a number that tells you how much of the variance (variation) in one or the other of the variables is "explained" by the other.  So, for example, the .70 correlation above tells us that 49% of the variation in homicide rates is related to the ownership of hand guns.  That leaves us with 51% of the variation we still need to account for.

In psychology, we are generally impressed by correlations of .3 and higher.  .8 or .9 blows us away.

But one thing correlation cannot tell you is causality.  Your grades and your SATs correlate pretty well -- but which causes which?  Even the homicide-hand gun example doesn't give you causation.  Odds are always that there is something else that causes (or partially causes) two things to correlate.  Perhaps coming from richer parents leads to both good grades and high SATs.  Maybe a violent culture leads to both more guns and more violence.  It takes other kinds of research -- most especially experiments -- to pin down cause and effect!

---

© Copyright 2005, C. George Boeree