Descriptive Statistics

Descriptive statistics

Dr. C. George Boeree

Descriptive statistics are ways of summarizing large sets of quantitative (numerical) information. If you have a large number of measurements, the best thing you can do is to make a graph with all the possible scores along the bottom (x axis), and the number of times you came across that score recorded vertically (y axis) in the form of a bar. But such a graph is just plain hard to do statistical analyses with, so we have other, more numerical ways of summarizing the data.

Here is a small set of data: The grades for 15 students. For our purposes, they range from 0 (failing) to 4 (an A), and go up in steps of .2.

John -- 3.0
Mary -- 2.8
George -- 2.8
Beth -- 2.4
Sam -- 3.2
Judy -- 2.8
Fritz -- 1.8
Kate -- 3.8
Dave -- 2.6
Jenny -- 3.4
Mike -- 2.4
Sue -- 4.0
Don -- 3.4
Ellen -- 3.2
Orville -- 2.2

Here is the information in bar graph form:

Central tendency

Central tendency refers to the idea that there is one number that best summarizes the entire set of measurements, a number that is in some way "central" to the set.

The mode. The mode is the measurement that has the greatest frequency, the one you found the most of. Although it isn't used that much, it is useful when differences are rare or when the differences are non numerical. The prototypical example of something is usually the mode.

The mode for our example is 3.2. It is the grade with the most people (3).

The median. The median is the number at which half your measurements are more than that number and half are less than that number. The median is actually a better measure of centrality than the mean if your data are skewed, meaning lopsided. If, for example, you have a dozen ordinary folks and one millionaire, the distribution of their wealth would be lopsided towards the ordinary people, and the millionaire would be an outlier, or highly deviant member of the group. The millionaire would influence the mean a great deal, making it seem like all the members of the group are doing quite well. The median would actually be closer to the mean of all the people other than the millionaire.

The median for our example is 3.0. Half the people scored lower, and half higher (and one exactly).

The mean. The mean is just the average. It is the sum of all your measurements, divided by the number of measurements. This is the most used measure of central tendency, because of its mathematical qualities. It works best if the data is distributed very evenly across the range, or is distributed in the form of a normal or bell-shaped curve (see below). One interesting thing about the mean is that it represents the expected value if the distribution of measurements were random! Here is what the formula looks like:

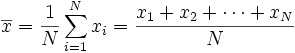
$\overline{x} = \frac{1}{N}\sum_{i=1}^N x_i = \frac{x_1+x_2+\cdots+x_N}{N}$

So 3.0 + 2.8 + 2.8 + 2.4 + 3.2 + 2.8 + 1.8 + 3.8 + 2.6 + 3.4 + 2.4 + 4.0 + 3.4 + 3.2 + 3.2 is 43.8. Divide that by 15 and that is the mean or average for our example: 2.92.

Statistical dispersion

Dispersion refers to the idea that there is a second number which tells us how "spread out" all the measurements are from that central number.

The range. The range is the measure from the smallest measurement to the largest one. This is the simplest measure of statistical dispersion or "spread."

The range for our example is 2.2, the distance from the lowest score, 1.8, to the highest, 4.0.

Interquartile range. A slightly more sophisticated measure is the interquartile range. If you divide the data into quartiles, meaning that one fourth of the measurements are in quartile 1, one fourth in 2, one fourth in 3, and one fourth in 4, you will get a number that divides 1 and 2 and a number that divides 3 and 4. You then measure the distance between those two numbers, which therefore contains half of the data. Notice that the number between quartile 2 and 3 is the median!

The interquartile range for example is .9, because the quartiles divide roughly at 2.45 and 3.35. The reason for the odd dividing lines is because there are 15 pieces of data, which, of course, cannot be neatly divided into quartiles!

The standard deviation. The standard deviation is the "average" degree to which scores deviate from the mean. More precisely, you measure how far all your measurements are from the mean, square each one, and add them all up. The result is called the variance. Take the square root of the variance, and you have the standard deviation. Like the mean, it is the "expected value" of how far the scores deviate from the mean. Here is what the formula looks like:

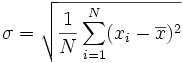
$\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \overline{x})^2}$

So, subtract the mean from each score and square them and sum: 5.1321. Then divide by 15 and take the square root and you have the standard deviation for our example: .5849.... One standard deviation above the mean is at about 3.5; one standard deviation below is at about 2.3.

The normal curve

At its simplest, the central tendency and the measure of dispersion describe a rectangle that is a summary of the set of data. On a more sophisticated level, these measures describe a curve, such as the normal curve, that contains the data most efficiently.

This curve, also called the bell-shaped curve, represents a distribution that reflects certain probabilistic events when extended to an infinite number of measurements. It is an idealized version of what happens in many large sets of measurements: Most measurements fall in the middle, and fewer fall at points farther away from the middle. A simple example is height: Very few people are below 3 feet tall; very few are over 8 feet tall; most of us are somewhere between 5 and 6. The same applies to weight, IQs, and SATs! In the normal curve, the mean, median, and mode are all the same.

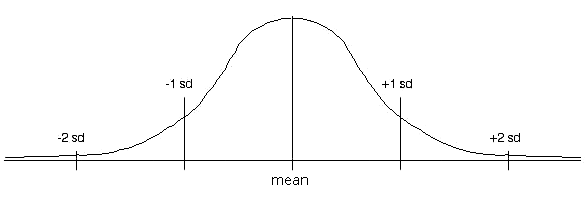
One standard deviation below the mean contains 34.1% of the measures, as does one standard deviation above the mean. From one to two below contains 13.6%, as does from one to two above. From two to three standard deviations contains 2.1% on each end. An other way to look at it: Between one standard deviation below and above, we have 68% of the data; from two below to two above, we have 95%; from three below to three above, we have 99.7%

Because of its mathematical properties, especially its close ties to probability theory, the normal curve is often used in statistics, with the assumption that the mean and standard deviation of a set of measurements define the distribution. Hopefully, it is obvious that this is not at all true for nearly all cases. The best representation of your measurements is a diagram which includes all the measurements, not just their mean and standard deviation! Our example above is a clear example - a normal curve with a mean of 2.92 and a standard deviation of .58 is quite different from the pattern of the original data. A good real life example is IQ and intelligence: IQ tests are intentionally scored in such a way that they generate a normal curve, and because IQ tests are what we use to measure intelligence, we often assume that intelligence is normally distributed, which is not at all necessarily true!