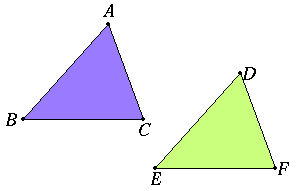
This is the familiar side-angle-side congruence proposition for triangles. When two triangles have two sides and the included angle equal, then the remaining sides, angle, and area are also equal, that is to say, they're congruent. Symbolically, given triangles ABC and DEF with AB = DE, AC = DF, and angle BAC = angle EDF, then the rest of the parts of the triangles are the same.
Euclid's proof of this proposition relies on the "principle of superposition". This principle is not supported by his postulates, and so it would be more appropriate to take I.4 as a postulate than pretend that it is adequately justified by its proof. For more discussion on this point, see the Guide for I.4.
There will be two other congruence propositions: I.8, side-side-side, and I.26, side and two angles.
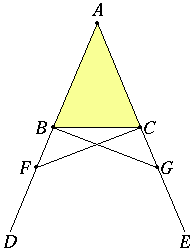In the figure AB = AC, so triangle ABC is isosceles.
One of the properties of such triangles is that they also have two equal angles, the base angles of the triangle, angles ABC and ACB. That's the first part of the statement of Proposition I.5. The other conclusion is that the angles supplementary to the base angles are also equal, that is, angles DBC and ECB are equal.