That isn't to say that ratios of different kinds of magnitudes aren't equated. In fact, that's one of the more important aspects of ratios. For example, the fundamental proposition of Book VI, proposition VI.1, says that given two triangles of the same height, the ratio of the triangles A:B is the same as the ratio of their heights Ah:Bh. That says that the ratio of two plane figures equals the ratio of two lines.
Now, a common operation on proportions (equalities of ratios) is that of alternation (see V.Def.12 and V.16) which in its general form says that if A:B = C:D, then A:C = B:D. In the Elements alternation only applies when all four quantities are of the same kind. But if alternation is applied to the proportion of VI.1, then we get A:Ah = B:Bh, the equality of two mixed ratios, ratios of plane figures to lines. This step, and the acceptance of mixed ratios, which seems to us like a small thing, was not taken until centuries after Euclid.
Since equality and order are defined, their expected properties are proved in propositions, or at least some of the properties. For example, proposition V.11 states that two ratios that are the same as a third are the same as each other, a statement analogous to C.N.1 for magnitudes.
The process used for defining ratios of magnitudes was something new for Eudoxus and Euclid, but that process is now commonplace in mathematics to construct new kinds of things. The process starts with entities x, y, z, etc., that are well understood, such as pairs of magnitudes of the same kind. Then a relation E on these entities is found which is intended to be equality for them. For ratios, that is given in V.Def.5. Right now, let xEy denote that x is related to y by the relation E. Next, it is verified that the relation E is an equivalence relation, that is, a reflexive, symmetric, and transitive relation.
A relation E is reflexive if for any x it is the case that xEx, that is, anything is related to itself by E. A relation is E is symmetric if whenever xEy, then yEx. And it is transitive if whenever xEy and yEz, then xEz.
Once E is known to be an equivalence relation, new entities are conceived which are named by the old entities x, y, z, etc., but the new entities are taken to be equal, x = y, when their names are equivalent under the relation E, that is, xEy. Proportion as an equivalence relation is discussed in the Guide to definition V.Def.5.
Numbers can be added and subtracted, and so can magnitudes of the same kind, but ratios cannot. Take for example a ratio A:B of plane figures and a ratio C:D of angles. What could be meant by their sum (A:B) + (C:D)? One obvious approach is to treat ratios as quotients. That suggests A/B + C/D = (AD + BC)/BD, but a product of a plane figure and an angle, such as AD, has no meaning, so the obvious approach has obvious difficulties.
Multiplication and division are not automatic for ratios. Ratios A:B and B:C are compounded to form A:C, which may be thought of as the product of the two ratios, and the duplicate ratio mentioned above is a special case of a compound ratio. But the compound of two ratios A:B and C:D depends on the middle terms B and C being the same. The proof of proposition V.18 assumes that fourth proportionals exist, a property unjustified by any postulate, but if fourth proportionals do exist, then the ratio C:D is equal to some ratio B:E, and then the compound of A:B and C:D is the compound of A:B and B:E, and that compound is A:E. Thus, multiplication is an operation when fourth proportionals exist. Division is also an operation when fourth proportionals exist since D:C may be thought of as the reciprocal of C:D.
Numeric ratios, that is, ratios of numbers, are treated in the books on number theory, Books VII through VIII. In modern terminology these numeric ratios are called "positive rational numbers." Numeric ratios and proportions have a separate, simpler definition in VII.Def.20. That definition is compatible with the definitions here in Book V, but that compatibility is not demonstrated in the Elements.
The problem with numeric ratios is that there are not enough of them. That is ratios of magnitudes are not always equal to ratios of numbers.
| The illustration to the right shows a square with side A and diameter B. The ratio B to A does exist according to the next definition V.Def.4 since some multiple of each is greater than the other. In modern terms this ratio would be identified with the square root of 2 and is known to be an irrational number, that is, it is not equal to a numeric ratio. It is, nonetheless, a ratio in Euclid's terminology. The ratio B:A is a ratio of lines, but it is not a ratio of numbers. |
Since this and other ratios of lines are not ratios of numbers, a more general definition of ratio is required. That more general definition is the one given here and continuing through V.Def.6.
In modern terminology, the numeric ratios are positive rational numbers. The field of all rational numbers including 0 and the negative rational numbers is commonly denoted Q. The ratios of lines constructable in plane geometry form the field extended from Q by closure under square roots. A convenient notation for that field is Q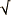
. It is a much larger field, but does not include all real numbers. For instance, the cube root of 2, needed for doubling a cube, the sine of 20°, needed for trisecting angles, and pi, needed for squaring the circle, all are missing from Q.
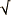The conic sections are part of solid geometry but they are not treated in the Elements. Cones are discussed in Book XII, but their sections (intersections with planes) which include ellipses, parabolas, and hyperbolas are not even defined in the Elements. Euclid's work on the Conics was superceded by Apollonius' and no longer exists. Intersections of conics lead to lines of new lengths that can be used to solve problems such as doubling a cube and trisecting an angle, but they don't help in squaring the circle. Thus, there are more ratios of lines constructable in solid geometry than ratios of lines constructable in plane geometry.
The ratios of rectilinear figures form the same field Q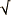 as the ratios of lines. This follows from the theory of application of areas developed in Book I, see proposition I.44. But there are other plane figures besides rectilinear ones: circles. The ratio of a circle to the square on its radius is pi. Thus, pi is a ratio of plane figures even though it is not a ratio of lines.
Book V Introduction - Definitions V.Def.1 and V.Def.2 - Definition V.Def.4.