Introduction

In this module you will be introduced to the basic Excel functions used in financial analysis. Many users find these functions somewhat more difficult to use than the mathematical or statistical functions primarily because they don't work in a finance or accounting environment. However, they can be very useful in your professional and personal life.

The basic financial functions will be briefly explained and some examples provided. Do not be shy about using the Excel Help feature for more in-depth explanations. You will be asked to complete assignments which require their use primarily in personal finance situations. I have chosen this approach because the situations are more familiar. The results can be useful in many personal decision-making situations and the knowledge acquired should easily transfer to business situations.

Some Financial Functions

Two confusing concepts are the present value and future value of investments. Let's look at future value first. The future value function in Excel will return the value of an investment based on regular, constant payments at a fixed interest rate. The function looks like this: =FV(rate,nper,pmt,pv,type) (The arguments in bold are required)

Suppose you want to find out how much you will have at the end of five years if you put $100 into an investment account at the beginning of every month with a 7.75% annual rate of return. You open the account with an initial investment of $4000. The resultant function would be =FV((0.0775/12), (5*12), -100, -4000, 1) and would return $13,232.98. Notice that the rate is a monthly return since we are depositing on a monthly basis. The nper (number of periods) ends up being 60 months - your could simply type in 60 rather than (5*12). The monthly investment (pmt) is $100 but you have to input it as -100. You will get an error if you use a $ sign and it has to be negative because that is the present value to you ($100 out of your pocket) when you invest it. The same goes for the present value (PV) - the current value to you is negative $4000 since it is out of your pocket. Finally, type is either 0 or 1 depending on when you invest it. Select 1 if you invest at the beginning of the month; 0 if you invest at the end of the month. If you leave this argument out, it defaults to 0.

The present value function is similar, =PV(rate,nper,pmt,fv,type), and returns the value that a series of future payments is worth now. Suppose you want to purchase a long-term care policy that starts immediately and pays $170 at the beginning of every month for 3 years. The initial cost is $6000 and the account will pays a paltry 4% on the account balance. =PV(0.04/12, 36, 170, ,1) will return -$5758.03. Since the present value ($5758) is less than you are ask to pay ($6000), it is not a good investment.

We frequently want to find out how much monthly payments will be when we are considering purchasing a car or house. You've gotten a raise but can you afford that new $52,000 Lexus? You really need a 5 year payoff period and they are offering nice 4.8% financing on the $52,000. You have to pay taxes, license, title, etc up front. To find your monthly payment use =PMT(rate,nper,pv,fv,type). =PMT(0.048/12, 60, -52000) will return your payment of $976.55.

OK, so you can't afford that so maybe you could stretch your payments over a little longer time. You figure you can afford $900 per months and want to know how long your payments would be. Use the number-of-periods function, =NPER(rate, pmt, pv, fv, type). =NPER(0.048/12, -900, 52000) returns 65.83 months. Notice that 52000 is positive since the present value to you is $52000.

You can use analysis similar to above to find a particular interest rate using =RATE(nper,pmt,PV,fv,type,guess). The guess argument is your best guess as to what the rate will be. Because of the mathematics a close guess helps Excel converge to the value more quickly. It defaults to 10%.

The final two functions are associated with the PMT function. Using =PPMT(rate,per,nper,PV,fv,type) and IPMT(rate,per,nper,PV,fv,type) you can determine what part of each total payment is on the principle and which is interest on the balance.

Assignments:

For a maximum grade of B-:

1. Develop a spreadsheet that shows the payoff schedule on what might be a typical home mortgage loan of $200,000 at 8% for 30 years. The payoff schedule should have 360 rows, one for each month, and five columns (month, total payment, principle amount for that month, interest amount for that month and loan balance.

For a maximum grade of B

1. Complete the B- level assignment.
   
   
2. Many people do not understand the power of compound interest and the implications of investing while you are young. Completing this exercise might even convince you to forego that Beemer for a while and invest the money instead.
   
   You are 22 years old and taking your first job. You can live quite comfortably on the great salary you got (because you were an Information Systems major) and still invest $400 per month. You intend to save for only 10 years then let the money sit in your investment account for 30 more years and retire at age 62. You consider yourself an astute investor and feel you can get an average return of 12% every year. Calculate how much you will have after 40 years. (Invest monthly, at the beginning of the month, for 10 years, then calculate the value of your account monthly for the next 30 years)
   
   Your roommate, a history major, really wants a Beemer and figures that 25 years before (s)he reaches retirement is plenty of time to save and invest. How much will (s)he have at age 62 if (s)he invests $400 per month for 25 years starting at age 37? How much would (s)he have to invest each month to match your retirement fund at age 62 if (s)he starts saving at age 37? Assume 12% average annual rate of return.

For a maximum grade of B+

1. Complete the B level assignment.
   
   
2. On the web you can find dozens of retirement planning "helpers". You input how much you will save per year, the interest rate you expect, and the number of years you intend to save then the program computes how much you will have at the end of the period. A major fault with these is that many assume you get the same rate of return every year. Consider the following situation.
   
   A client wants to start investing for retirement, which is 40 years away. She is starting with $0 but will invest $2400 per year (at the beginning of each year) and expects an average rate of return of 10%. Using Excel, you should compute the amount as $1,168,444, a nice tidy sum, at the end of 40 years. However the final amount really depends on the interest rate from year to year and not on the 40 year average. Your client tells you that she needs at least $1,000,000 when she retires. Although you would expect her to have about $1.168 million you should still tell her the probability of not reaching the $1,000,000 figure. Estimate that probability. Let the rate of return from year to year be normally distributed with mean 10% and a standard deviation of 3%. Generate the return after 40 years, using randomly generated return rates for each year, at least 1000 times and use your results to estimate the probability of not reaching the $1,000,000 minimum. What is the minimum amount she would have to save every year to have a probability of at least 95% of achieving her goal of $1,000,000? Include a scatter plot of the average return over the 40 year period and the account value at the end of 40 years. Briefly comment on the different account values for the same average return.

For a maximum grade of A-

1. Complete the B+ level assignment.
   
   
2. Eventually you are going to buy a house and will be faced with myriad decisions such as how long to finance (30 years, 20 years, bimonthly payments, 15 years, etc.) and how much to put down (minimum, 10%, 20%, etc.) (This is an aside, but important - If you put less than 20% down you will probably have to buy mortgage insurance which is very expensive. Frequently, when you put less money down, you can drop the mortgage insurance after a few years once your equity in the house reaches 20%. But, you have to ask - lending institutions don't usually tell you that.) Another decision is what loan rate and "points" choice to make. A "point" is 1% of the loan amount paid up front. Your decision will require a complex analysis of your tax bracket, investing philosophy, personality, long term financial goals, age, and many other variables. Regardless, you would still want conduct an analysis of the various rates and points as well as other factors you could quantify.
   
   Using the four options below conduct a basic analysis that shows the financial tradeoffs for each choice. Assume you are borrowing $200,000 with nothing down and that the bank will include the points in your loan if you elect a lower rate, (see rate/points table below). (Aside: Depending on the lending institution, points may be "tacked onto" the loan so you are simply borrowing a larger amount at a lower rate or deducted from the loan amount so you have to make up the difference at closing.) In your analysis, assume that you will invest the difference between the highest payment ($1538, the payment on $200,000 at 8.5% for 30 years) and each of the others and get a 10% return.
   
   

Rate	Points
8.5%	0
8.0%	2.5
7.25%	3.75
7.0%	5.25


Hint: Set up your spreadsheet so that each option has a column for interest payment, principle payment, loan balance, amount in investments (except for 8.5%), and loan balance minus investments (You would use your investments to pay down the mortgage principle.).

In the example below, I compared the loan balances (minus investment value) for two rates. Your graph should look something like this, but with 4 curves. Again, the "Loan amount remaining" is really the loan amount remaining minus what you have in your investments as this amount could be used to pay down the mortgage principle. What decision would this graph help you make?



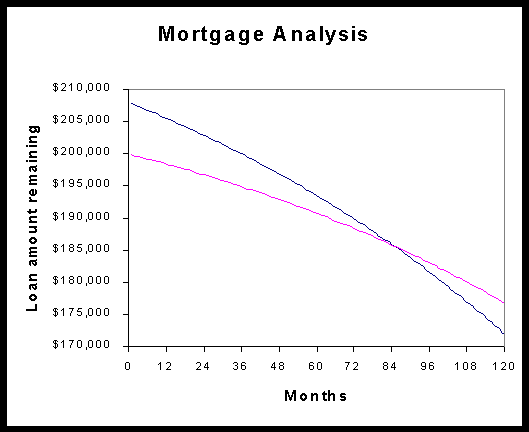
Note: This analysis is not too practical by itself.. One of the most critical factors in deciding home ownership is the impact of taxes. Interest on mortgage payments are tax deductible. For the 8.5% option the interest during the first year is $16,942. If you are in the 20% tax bracket, you can deduct this and pay $3388 less in taxes. You must account for this when you do this in real-life situations. The important decision of paying off a mortgage or putting the money into savings gets complex but you can use this exercise as a starting point. Also, look at the total amount of money you pay in interest - most people are not aware of this. At 8.5% for 30 years it is $353,618, approaching twice the amount of the original loan!

For a maximum grade of A

1. Complete the A- level assignment.
   
   
2. In both your professional and personal life you will probably be faced with a decision on whether it is better to lease or buy equipment. A lease or buy decision involving copiers and computers is frequently encountered by businesses. In your personal life you may have wondered whether you should lease an automobile or buy it. This is your opportunity to conduct a lease or buy analysis. This is a very flexible assignment and you have lots of latitude. I encourage you to be as creative as necessary in both selecting a situation and conducting the analysis. My goal is to have you get a feel for the many considerations that must be taken into account in a lease vs buy decision. If you would like to perform an analysis of lease Vs buy involving a situation you have encountered at work, feel free. If not, consider a lease Vs buy analysis for an automobile as an alternative.
   
   Here are some hints if you elect to analyze an automobile lease vs buy decision. Choose a make and model of a new car you want to possess. You can find the cost to purchase and cost to lease a vehicles in the newspapers or on the web. If you use the web, determine the invoice price and MSRP of the car with the options you want; www.edmunds.com and www.kbb.com should have the information. Assume you will purchase the vehicle at a price that splits the difference between the invoice price and MSRP. (Don't forget to add the destination charges.) Add 6% sales tax plus $100 for title, license, etc. You are going to put 10% down and finance the balance at 8% for 72 months. You intend to keep the car for 6 years. Now, go to the web and find the trade-in value for that, or similar, model car that is 6 years old. (Assume you drive 12,000 miles per year and the car will be kept in excellent condition.) This will allow you to estimate your depreciation. With this information you should be able to get a very good estimate of the cost of ownership for 6 years, ignoring insurance, maintenance, fuel, etc.
   
   Compare the cost of ownership with that of leasing. Assume the upfront cost of a lease is 10% of the MSRP. Typically, cars are leased for three years so you will have to lease another and incur appropriate costs at the three year point. You have to be careful here to find and include all the hidden costs in leasing. Several web sites provide that information. Conduct a financial analysis that compares the costs over the 6 year period. In your write-up, include the info about your vehicle in the assignment - I'm just curious about what type of car you envision yourself in. Find a site online that will conduct the analysis for you. How do your results compare with the online results? What site did you use? Include this information in your write-up also.