Math 326 Project 2b -
Pipe Dream - due November 20
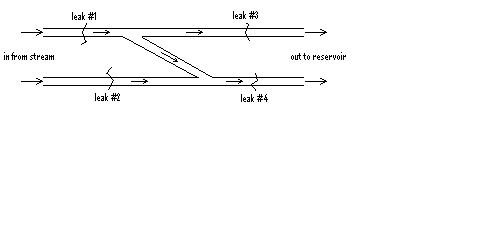
The system of pipes bringing water from a nearby stream to your reservoir
has sprung a variety of leaks. You have cobbled the pipes together over the
years so they now form the complicated pattern pictured below.
Searching around for extra pipes you can use for repairs, you finally find
four pieces. Two pieces are "good", which will work 90% of the time; the other 10%
of the time they leak and no water gets through. The other two pieces are "bad",
these pieces only work 70% of the time.
There are six different configurations for assigning the good or bad repairs among
the leaks. Use a simluation to test each configuration to determine the probability some water
will get through (note, for example, if leaks #2 and #3 fail but leaks #1 and #4 hold,
then water gets through).
A simulation is made up of a large number of trials. In each trial, use random numbers to determine if each leak works or fails. RAND() generates a random number between 0 and 1. For example, a "good" piece would succeed if RAND()<0.9. Based on which leaks work, determine if water gets through on that trial. Then repeat a large number of times to approximate the probability water gets through with that configuration.
Which is the best configuration? Can you think of a
reason why this should be the best?
Your written report should be no more than two pages in length, and
should contain the following:
Description of the problem:
Be sure to include any assumptions you've made, and be specific.
Description of the model:
Introduce notation and variables you will be using. Focus on the
interaction of the variables, how they are updated.
Data and results: Provide a
summary of your results. Include a graph or table supporting your
findings.
Closing: Here you could
briefly
summarize the problem and your results, or include possible
improvements and other comments about your model.
HINT: You can estimate the probability using simulation of a large number of trials, as in 7.4.
Calculating the exact probability is possible, but run the simulations is easier.
