Intermediate Answers to Exercise 10.1-1

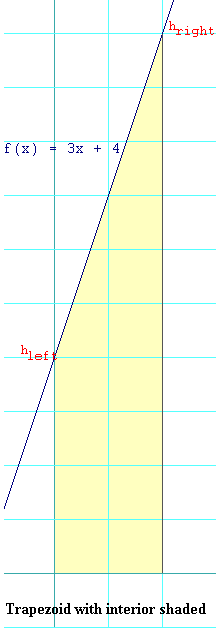
See the figure on the right to visualize what area this problem is dealing with. Notice that the lower base of the trapezoid in the figure is length 2 (scroll down a bit to see the bottom of the figure if you need to). If you divide something of length 2 into n sections, each section will be of length  2/n.

We are finding at what x the left-hand edge of the kth slice is. The first slice has its left-hand edge at the origin, or at  x = 0.  The second is at  x = 2/n.  The third is at  x = 4/n.  The fourth is at  x = 6/n.  See the pattern? The left-hand edge of the kth slice will be at  x = 2(k-1)/n. 

You know that the x for the left-hand edge of the kth rectangle is  2(k-1)/n.  So put that as x into  f(x) = 3x + 4.  You get

   hk  =  f(x)  =  f(2(k-1)/n)  =  (6(k-1)/n) + 4

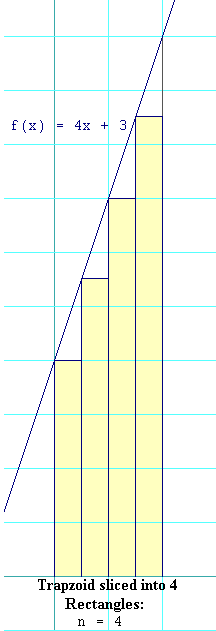
The figure on the right shows the trapezoid sliced into 4 strips (that is,  n = 4 ) with each strip approximated by a rectangle. The height of each rectangle is f(x), where x is where the left-hand edge of the rectangle is. Now we find the area of the kth rectangle (where k starts at 1 for the left-most rectangle and counts up). You've got the width from step 1 as 2/n. You've got the height of the kth rectangle from step 3 as  (6(k-1)/n) + 4.  The area of a rectangle is base times height. So the area of the kth rectangle, A_k, is given by

   Ak  =  (2/n) ( (6(k-1)/n) + 4 )

       =  (12(k-1)/n2) + (8/n)

You have an expression for the area of the kth rectangle, A_k, from step 4. And you know that k ranges from 1 to n. So the sum over A_k is

              n
   Atotal  =  å Ak
             k=1

              n
   Atotal  =  å (12(k-1)/n2) + (8/n)
             k=1

From step 5, the thing you have in the summation is the sum of  12(k-1)/n²  and  8/n.  So you just break it into two summations using two sigma-expressions:

              n                 n
   Atotal  =  å 12(k-1)/n2  +  å 8/n
             k=1               k=1

From step 6, you had the sum over k of  12(k-1)/n²,  and the sum over k of  8/n.  In the case of the first expression, the factor that is constant with respect to k is  12/n².  For the second one, the whole expression,  8/n,  is constant with respect to k, so it all comes out. This gives you

                      n                n
   Atotal  =  (12/n2) å k-1  +  (8/n) å 1
                     k=1              k=1

From step 8 you have that the approximate area is  14 - 6/n.  You need to take the limit as n goes to infinity. Well 14 is a constant, and it is not affected by the value of n. So the 14 stays. But the 6/n gets closer and closer to zero as n gets huge. So in the limit, the 6/n becomes insignificant and you are left with the value we expected all along of 14. And lo, in the limit, the approximate area becomes the actual area once again.

I'd like you to try this problem again on your own, but instead of taking the area bounded on the right by  x = 2,  I'd like you to bound it on the right at  x = a,  where a is an arbitrary positive number. This is the way we did the sample problem in the text, so follow that example. You will do everything you did in this coached example, except instead of using 2 as a boundary, you will use a. You should end up with an expression that is a function of a. You can check your answer by observing that the length of the base of the trapzoid is a, the left-hand height is still 4, and the right-hand height is now f(a). Use the formula for the area of a trapezoid to determine what your answer ought to be. Does the answer you get from slicing and taking the limit match? If not, go back and review to see where your mistake is.