A Derivative Construction

Open a new GeoGebra worksheet.  Enter the function  f(x) = cos(3x) / (1 + x^2) .  Make the graph blue and a little thicker. Next, type  f '(x)  into the input bar.  GeoGebra automatically calculates the derivative of f(x). Select the New Point tool  and click anywhere on the graph of  f .  Color the point red. Select the Tangent Line tool then click on the point and the function f .  Make the tangent line dashed.
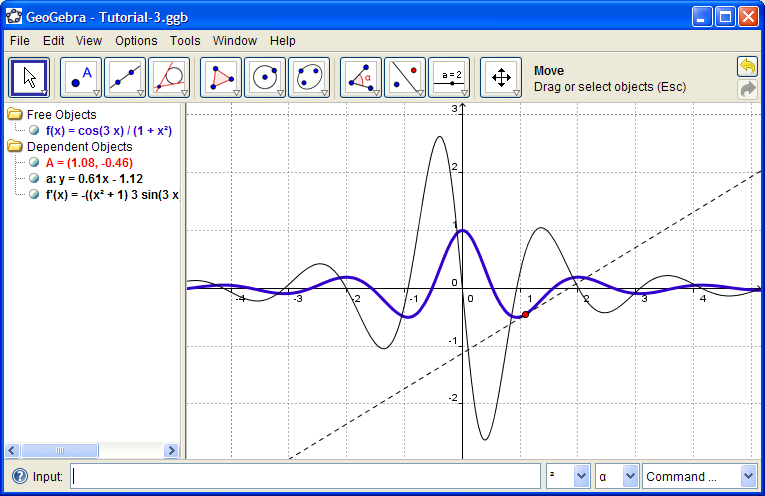
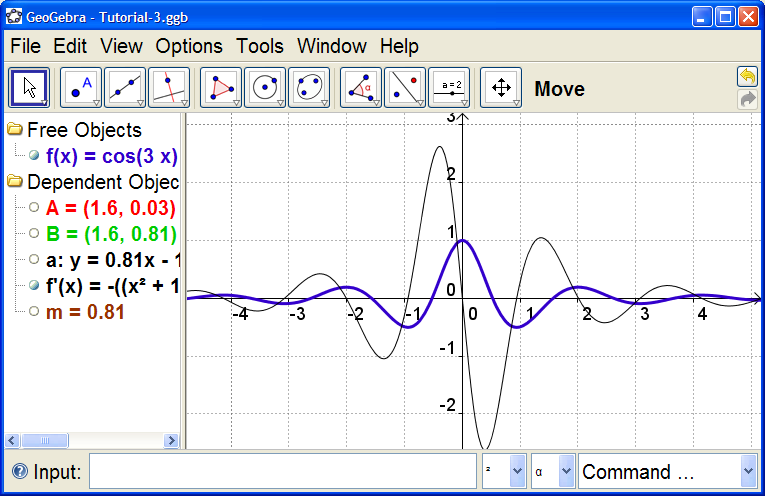
Select the Slope tool and click the line.  In the Algebra View, click the circle next to  m  to hide the slope. Select the Text tool and enter     "Slope of tangent: " + m Increase the size of the text, if you wish. Hide the graph of  f '(x). In the Input Bar, type  ( x(A), m ).  This creates a point B whose x-coordinate is the x-coordinate of A (the red point on f) and whose y-coordinate is m.  As we drag point A, point B follows the derivative curve.  Make B green. Right-click point B and select "Trace On".  Now, as A is dragged, B leaves a record of its path.  You can hide/unhide the graph of  f '(x)  to confirm that this really is the graph of the derivative.
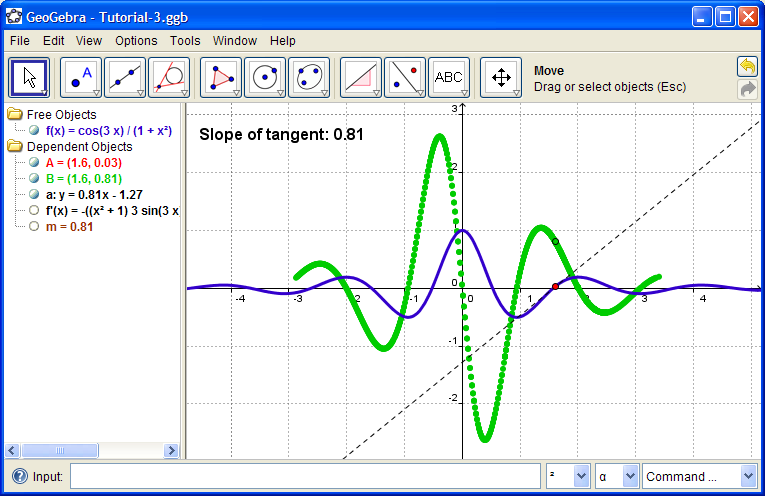
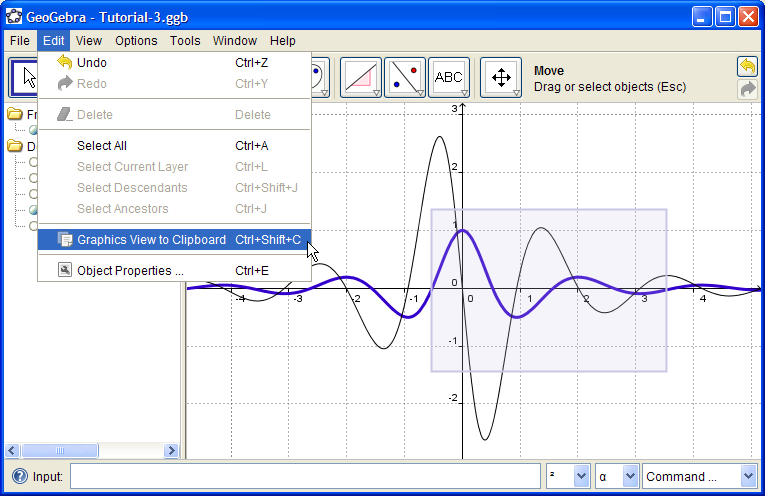
Turn off tracing on B, and from the View menu, choose Refresh Views to remove the trace of point B. Hide everything except for f and f '.  To copy the entire Graphics View to the clipboard, choose the menu Edit > Graphics View to Clipboard.  Then you can paste the picture into another program. Often it's useful to capture only a portion of the Graphics View.  If you click and drag a rectangle first, then only the portion of the Graphics View in the rectangle gets copied to the clipboard.  For instance, I might copy the view on the right and put it into a quiz where I ask students to identify which graph is f and which is f '.
Finally, suppose you want to use this worksheet as part of a classroom presentation.  You can increase the size of the screen elements by selecting Options > Font Size.  Now the people in the back of the classroom can see what you're doing!

• If you have a point A, then the functions x(A) and y(A) will return the x- and y-coordinates of A.
• If you type in an object, like  4x + 1  or  (4, 2)  GeoGebra will automatically name it.  You can supply a name, too, like g(x) = 4x + 1 or P = (4, 2).