2.4 Limits on the Side
Think about the function,
_
f(x) = Öx
In the real numbers we can only
define it for
x ³ 0. This is illustrated in the graph.
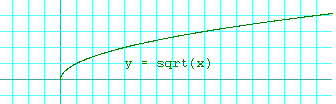 Notice that no function is graphed to the left of zero.
Notice that no function is graphed to the left of zero.
But what about the behavior of this function at zero? We
do define
Ö0 = 0. But does this function have
a limit at
x = 0? From our previous discussions, we would say
that we have a limit at
x = 0 if, as x gets close to zero,
Öx gets close to the limit, which, in this case, we would
like to believe is zero as well. But isn't -0.0000001 close
to zero? The problem is, -0.0000001 is negative, and
Öx is undefined for
x < 0. With this function, x can
only get close to zero from the positive side. And so we define a
special one-sided limit, which we annotate as:
_
lim Öx = 0 eq. 2.4-1
x > 0+
In contract form, this means that for any
e > 0 you might choose, no matter how
small, I can find a
d > 0 small enough that
_
|Öx - 0| £ e eq. 2.4-2
whenever 0 < x - 0 £ d. Notice that we have
removed the absolute value sign and resticted the difference to being
positive in the "whenever" clause of the contract.
And in general, what we mean by (which is spoken as, "the limit of f(x)
as x goes toward a from above.")
lim f(x) = L eq. 2.4-3
x > a+
is the following contract: for any
e > 0 you might name, no matter how small, I can
find a d > 0 small enough that
|f(x) - L| £ e eq. 2.4-4
whenever 0 < x - a £ d. Note that this
definition allows that x approach a only for values
for which x > a. This is in contrast to a
standard limit in which x can approach a from either
side and arrive at the same limit either way.
Of course, by symmetry, we might have another case in which we would like
to approach the limit from below. So what we mean by (which is spoken as, "the limit of f(x)
as x goes toward a from below.")
lim f(x) = L eq. 2.4-5
x > a-
is the following contract: for any
e > 0 you might name, no matter how small, I can
find a d > 0 small enough that
|f(x) - L| £ e eq. 2.4-6
whenever 0 < a - x £ d. Notice that the
only difference between this contract and the one in 2.4-4 is that we
have turned the difference between x and a around in
the "whenever" clause. And that resticts the contract to values of x
that are less than a.
Exercise
Prove that 2.4-1 is true using the contract in 2.4-2.
Return to Table of Contents
Move on to A Most Useful Rule
email me at hahn@netsrq.com


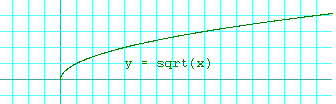 Notice that no function is graphed to the left of zero.
Notice that no function is graphed to the left of zero.