Box 10-2: Finding the Area Under the Square Root Curve

Divide and Conquer

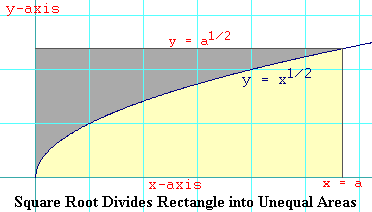
Square Root Divides Rectangle into Unequal Areas

The figure shows the square root function with the rectangle drawn and the two unequal areas shaded. The area we are interested in finding is shaded in yellow. The area that constitutes the rest of the rectangle is shaded gray. We already know that the Rieman sum method will not help us much in evaluating the yellow area because we end up with a summation that we don't know how to do. But the total area of the rectangle is clear. We know its base and its height, so when we take their product we get:

            _
   A_rectangle  =  a Öa  =  a(a^1/2)  =  a^3/2

We also know that the sum of the gray and yellow areas has to equal the total area of the rectangle:

   A_rectangle  =  a^3/2  =  A_gray  +  A_yellow


   A_yellow  =  a^3/2  -  A_gray

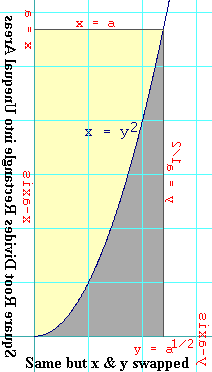So if we can find the gray area, we can solve this problem. Do you see anything familiar about the gray area? Perhaps if we rotate and flip the diagram you'll see it. The second diagram shows how rotating and flipping the drawing has the effect of swapping the x and y axis. Do you remember the trick from algebra for finding the graph of the inverse function? This was where you rotated the paper ninety degrees and then viewed it from the back. The writing appeared backwards, but the graph that you saw was that of the inverse function. By rotating and flipping the graph of the square root function, we see its inverse, which is the square function.

Now finding the gray area looks a whole lot like finding the area under the f(x) = x² curve. But instead of finding the area bounded on the right by x = a, now we area find the area bounded on the right by y = a^1/2. When the area was bounded by x = a, we got area of A = a³/3. That is, we cubed the width of the area and divided the result by 3. Since the gray area is precisely the same shape, we should do the same thing. This time the width is not a, but a^1/2. So we cube that and divide by 3.

   A_gray  =  ((a^1/2)³)/3  =  (a^3/2)/3

And to find the yellow area, we simply go back to the previous equation:

   A_yellow  =  a^3/2  -  A_gray  =  a^3/2 - (a^3/2)/3  =  (2/3)a^3/2

and that is the solution.

Return to main text

email me at hahn@netsrq.com