Box 10-2a: The Nitty Gritty of the Fundamental Theorem

This page contains optional material that won't be on your exam.

On first blush it seems that we have proved the Fundamental Theorem of Calculus outright in the main text. But in reality we have made a hidden assumption, and without proving that assumption, there is no guarantee that a Riemann sum even has a limit as the number of rectangles goes to infinity.

The hidden assumption (and it is subtle) was that we could look at what happens with just one rectangle and then generalize to what happens with an infinite sum of them. It turns out that the condition of f(x) being continuous is enough to guarantee what we need for any rectangle in particular, but not enough for the infinite crowd of them that we end up with when we take the limit. There is a stronger form of continuity called uniform continuity that is required for the Riemann sum to be guaranteed a limit.

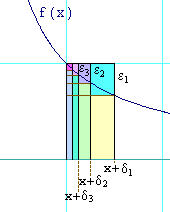
Function Height in Thinner and Thinner Rectangles

Look at what's happening in the diagram. The e's indicate how far the top of the rectangle is from the function at a distance, d, from x. If, for example, you chose the width of the rectangle to be d₁, then the height of the rectangle is within e₁ of the function on the right-hand edge. The worst the inaccuracy (which we'll call x) could possibly be when you approximate the area under the curve using that rectangle would be e₁ times the width of the rectangle:

   0  £  x₁  £  |e₁d₁|

You can see that if you demand a smaller e, then you require a smaller d. The diagram shows, for example, that the smaller e₂ requires you to use the smaller d₂ as the width of the rectangle. Continuity of f(x) guarantees that no matter how small an e you require, you can find a rectangle thin enough (that is a d small enough) to get it. That is, continuity will give you a recipe for finding a small enough d for as small an e as you like.

The problem lies in that the recipe is only guaranteed to work for this rectangle. Other rectangles in the Riemann sum might require a different recipe. So a d that guarantees a desired e for this rectangle might not give you as small an e at some other rectangle.

This is where the concept of uniform continuity comes in. Uniform continuity of a function over some domain of x says not only that the function, f(x), is continuous at every x in that domain, but additionally that for any e > 0 that you might name, I can come up with a d > 0 that will work uniformly at every x in the domain. That is this same d will assure that

   |f(x+d) - f(x)|  £  e

not just for a particular x, but for every x in the domain. In other words, the same recipe for finding d works everywhere in the domain where the function, f(x), is uniformly continuous.

With the Riemann sums we are approximating the area under the curve, f(x), within some interval of x. That interval is the domain over which we would like f(x) to be uniformly continous. Why? Suppose you name an e that must be the worst error for the height of any rectangle in the Riemann sum. Uniform continuity of f(x) says that we can find a single d to use as the width of every rectangle to ensure this.

Now what happens to the inaccuracy for the area of each rectangle as a result?

   0  £  x  £  |ed|

where x is the inaccuracy by which the rectangle misapproximates the area under the curve within its width. The neat thing is that this is the worst the inaccuracy can possibly be for any rectangle in the Riemann sum.

But what is d? If the length of the interval in which we are finding the area is L and we are using n rectangles, then

   d  =  L/n

So substitute that into the inequality and you get

   0  £  x  £  |eL/n|

And that is true for every one of the n rectangles. So what is the worst the total error can be when we add up those n rectangles? Just multiply the inequality by n.

   0  £  x_total  £  |eL|

Uniform continuity ensures that we can make e as small as we like by making the width of the rectangles small enough, and we can make the width as small as we like by making n big enough. The length of the interval, L, doesn't change by taking more rectangles. So no matter how small a x_total > 0 I might demand, you can find an n large enough to reduce the inaccuracy in Riemann sum to no worse than x_total. That is, as n goes to infinity, the inaccuracy, x_total, in the Riemann sum goes to zero in the limit. And that means that as n goes to infinity, the Riemann sum must, in the limit, go to the area under the curve.

But what about this uniform continuity requirement we are forcing onto f(x)? It's a lot tougher than just plain continuity. How do we guarantee that the function we have chosen to find the area under is uniformly continuous over the entire interval we are interested in?

There is a theorem (whose proof is well beyond first year students) that when a domain interval is closed and bounded (that is it includes the endpoints and has endpoints at both ends), then any function that is continuous on that entire interval is also uniformly continuous on that entire interval. If you are dying of curiosity for more information on this theorem, search the web for "Heine-Borel theorem," "Lebesgue covering lemma" and "Lebesgue number." But you do need to have had either a course in real analysis or a course in topology to be equipped for these ideas you will find there.

The great thing about all this is that closed and bounded intervals are exactly the domains we are interested in taking Riemann sums and their limits over. So as long as the domain interval is closed and bounded, the function you are finding the area under needs only to be continuous to qualify.

Return to main text

email me at hahn@netsrq.com