

Note: This page of Karl's Calculus Tutor
has recently been reorganized.
You can't build a house from the roof down. In order to learn calculus, you have got to be able to do algebra. If you have no confidence in your algebra ability, perhaps you ought to see your advisor about putting off calculus for a semester in order to get some remediation in algebra.
If you are not sure whether you need remediation or not, I recommend that you review the following material. If it all comes back to you, great. But if it brings back bad memories of never having understood it in the first place, consider your options carefully. You could be in over your head.
Whatever you do identically to both sides of an equation is fine, providing it is not dividing it by zero. So, for example, if you have:
y + a = 3x + b eq. c-1You can subtract b from both sides to get:
y + a - b = 3x eq. c-2Then you can divide both sides by 3 to get a solution for x:
y + a - bIf you know, for example, that a=14 and b=7, then for any value of y you could tell me the value of x.= x eq. c-3 3
If you have two equations, you can add them together (that is add the expressions to the right of the equals and add the expressions to the left of the equals and set those two expressions equal to each other).
y + a = 3x + b y = 4x - a eq. c-4By the same token, you can add the left side of the first equation to the right side of the second, and vice versa, and set those two expressions equal to each other. Likewise with subtraction and multiplication. With division, you can still do the same thing, but you must be aware that the results only count in the cases when the divisor is not zero.2y + a = 7x + b - a
When you take a sum times some multiplier, the multiplication is said to distribute over the sum. The general rule is
a(b + c) = ab + acSo, for example,
2(x + y) = 2x + 2yIf you take the product of two sums, you can still use the distributive law:
(p + q)(r + s) = (p + q)r + (p + q)s = pr + qr + ps + qsYou can also apply the distributive law in reverse. If you have an expression like
Division also distributes over addition:
a + b a bAnd both multiplication and division distribute over subtraction:=+c c c
a(b - c) = ab - ac a - b a b=-c c c
Whenever you have an equation in the form of
y = mx + b eq. c-x1you have the equation of a straight line. The m is called the slope. The b is called the y-intercept. Some examples are
The y-intercept, on the other hand, tells you where the line
will cross the y-axis. Whatever b is, the line will
cross the y-axis at
Often you will have an equation that is not exactly in the
3x + 5y = 15
5y = -3x + 15
3
y = - + 3
5
3
m = - b = 3
5
Sometimes you will be asked to find the equation of a line
that passes through a particular point and has a particular
slope. For example, finding the equation of the line that
passes through y = mx + b 5 = 3m + bsince m = 2
5 = 6 + b -1 = bAnd there you have the b you were looking for. So the equation of that line is
y = 2x - 1The shortcut method of doing this is simply, if a line has a slope, m, and must pass through the point, (h,k), write the equation
y - k = m(x - h)In the previous example, where
y - 5 = 2(x - 3) y - 5 = 2x - 6 y = 2x - 1Other times you may be asked to find the equation of a line that passes through two points,
y2 - y1
y - y1 = (x - x1)
x2 - x1
which you then convert to the
5 - 3 2
y - 3 = (x - 1) = (x - 1)
2 - 1 1
y - 3 = 2x - 2
y = 2x + 1
m = 2 b = 1
Of course whenever you do such a problem, you should check
it by plugging the coordinates of your points for x
and y into the equation and making sure it works. If it doesn't,
go back and check your work for mistakes.
Sometimes you will be asked to find the point at which two straight
lines intersect. Suppose you had
y = 2.0x - 1 y = 0.4x + 3Once you know x, all you have to do is substitute it into either of the two equations to get y.0 = 1.6x - 4 4 = 1.6x x = 2.5
y = 2x - 1 y = (2 × 2.5) - 1 y = 4So the point of intersection is
If you have an equation in the form of:
ax2 + bx + c = 0 eq. c-5You can solve for the values of x by applying the quadratic formula:
-b ± sqrt( b2 - 4ac )
x = eq. c-6
2a
or in the more readable graphics:
________
-b ± Öb2 - 4ac
x = eq. c-6
2a
(Click here to see the derivation of the
quadratic formula)
Of course, a, b, and c need not be nice neat symbols, as I have here, but each might be an entire expression. You need to recognize when something is in the form of:
(expression1) × x2 + (expression2) × x + (expression3) = 0and also to be able to massage equations like it into this form. You can always solve for x when you have something like this simply by using the quadratic formula, provided the value inside the square root sign is not negative (if it is negative, you can still find solutions using complex numbers, but we won't be discussing that until well into the program).
Suppose you have
ax2 + bx + c = 0 eq. c-7and you have applied the quadratic formula and discovered that the solutions for x are x1 and x2. That means that if you take:
(x - x1) × (x - x2) eq. c-8and multiply it out, then gather up like terms, you will get:
b c
x2 + x + eq. c-9
a a
For example, you have:
2x2 - 6x + 4 = 0 eq. c-10in which
(x - 1) (x - 2)and multiply it out using the distributive law (which you ought to know well), you get:
x2 - 3x + 2 eq. c-11which agrees with the above.
A polynomial is an expression in the form of:
Cnxn + Cn-1xn-1 + ... + C2x2 + C1x + C0 eq. c-12The Cindex values are called coefficients. The highest power of x, which in this case is n, is said to be the degree of the polynomial.
The quadratics given in the previous section were examples of 2nd degree
polynomials.
We can use the summation notation to express polynomials as well:
n å Cjxj eq. c-13 j=0You can add polynomials simply by adding the terms of like powers, term by term. For example:
x3 + 4x2 + 6x + 3
2x2 + 6x + 4
eq. c-14
x3 + 6x2 + 12x + 7
You can subtract one polynomial from another in the same way. Adding or
subtracting polynomials always gives you another polynomial. So does
multiplying two polynomials, which you must do using the distibutive
law. If the polynomials are of any degree higher than 2, it's a real
pain in the neck. Here I show the product of two 2nd degree polynomials.
(x2 - x + 1) × (x2 + 2x - 3) =
x4 + x3 - 4x2 + 5x - 3
eq. c-15
A rule of thumb when multiplying polynomials is that the degree of the product
is always the sum of the degrees of the two polynomials you multiplied. Here
we multiplied two 2nd degree polynomials and got a 4th degree as a result.
Polynomials can be factored. That is they can be shown to be the product of other polynomials. We have already seen in the last section how we can do that with 2nd degree polynomials using the quadratic formula. The fundamental theorem of algebra states that every polynomial, no matter what its degree, can be factored into the product of polynomials, all of which have degree no greater than 2. The theorem doesn't say how to do it, and, in general, there is no sure-fire recipe that will give you a factorization. And the fundamental theorem of algebra, for being so fundamental, is not easy to prove (and I will not do so in this section). In fact, every proof I've seen requires the use of calculus. I mention the theorem and what it asserts only because your calculus professor might assume that you already know it.
When a 1st degree polynomial can be factored out of a higher degree polynomial, the 1st degree polynomial is said to represent a root of the higher degree polynomial. Recall that a 1st degree polynomial can always be written in the form of:
A × (x - r) eq. c-16where A and r are both real numbers. If you factor such an expression out of a polynomial, the real number, r, is said to be a root of the original polynomial.
Polynomials take a real number in and give another real number out. If you stick in a value for x and do all the exponentiation, multiplying, and adding, you will get another value. For example, if you stick in 4.0 for x into:
x2 - 3x + 2 eq c-17you get the value 6.0. Try it. Any value you can stick in for x into any polynomial will always give you some value back. Because of this, you can graph polynomials.
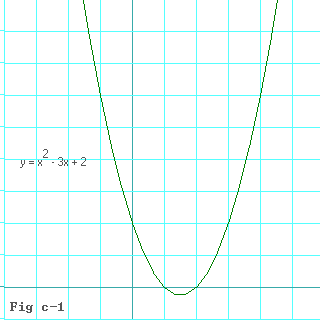
You can apply a procedure called polynomial long division in order
to divide a polynomial of greater degree by one of lesser degree. Suppose
you wanted to divide
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
Observe that the leading term of x - 1 (that is x)
divides the leading term of
2x2
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
Now multiply that quotient term by the divisor and write the negative of
the result
under the dividend, just as you do when you divide ordinary numbers.
Then do the implied subtraction (notice that we do the implied subtraction
by adding. That is because we wrote the negative of the product
on the bottom line).
2x2
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
-2x3 + 2x2
0 - 5x2
Observe that the leading terms exactly cancel. If they don't, you
did something wrong.
Now bring down the next term of the dividend, just as you do with
digits in numerical division
2x2
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
-2x3 + 2x2
-5x2 + 8x
and divide the leading term of the divisor into the leading term of
the expression on the bottom line here.
2x2 - 5x
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
-2x3 + 2x2
-5x2 + 8x
and again multiply the divisor by the new quotient term and write negative
of the result under the bottom line. Then do the implied subtraction.
2x2 - 5x
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
-2x3 + 2x2
-5x2 + 8x
5x2 - 5x
0 + 3x
Keep doing the procedure until you run out of dividend terms. In this
case we have to do it once more.
2x2 - 5x + 3
____________________
x - 1 ) 2x3 - 7x2 + 8x - 3
-2x3 + 2x2
-5x2 + 8x
5x2 - 5x
3x - 3
-3x + 3
0 + 0
Notice that in this case we got zero at the bottom line. That means it
divided evenly. Sometimes you will not get zero at the bottom line. When
that happens, whatever you're left with at the bottom line is called
the remainder (just as it was when you used long division on numbers).
The top line is the quotient. If you multply the quotient by the divisor
and then add the remainder, you will get the dividend -- always (unless,
of course, you've made a mistake).
Often you will be asked to factor a polynomial. This means that you must
find a term or terms in the form of
2x2 + 7x - 15You could find the factors by using the quadratic formula. Or you could remember that if
(a1x + b1)(a2x + b2) = 2x2 + 7x - 15Now remember that one of the a's must be 1 and the other must be 2. That is, the product of all the a's must be equal to the leading coefficient of the polynomial. The product of the b's must be -15, that is the product of the b's must be equal to the constant coefficient. So if one of the b's is ±3, the other must be ±5. You only have to decide which a goes with which b and what the signs of the b's are. The middle term of the polynomial can give you some help. It's coefficient is 7. And when you multiply out the factors you can see that
a1b2 + a2b1 = 7So try out the possible combinations in your head to see if you can make this equation true. When you hit on the combination that does it, you have factored the polynomial.
2×5 + 1×(-3) = 7 (2x - 3)(x + 5) = 2x2 + 7x - 15This method of using the middle term works with second degree polynomials (i.e., quadratics) only. If the polynomial is of higher degree, you will have to rely more on guess-work. But the rule of the factor,
x3 - 2x2 - 5x + 6You know that all the a's must be 1. For the b's your choices are ±1, ±2, and ±3. So you simply try a combination, say
x2 - x - 6Now all you have left to do is factor the quotient. Using the methods we have already discussed you can find that the remaining factors are
Factoring will not become easy for you unless you have practiced it.
The more polynomial factoring problems you do, the better you will
become at making the right guess on the first or second try. And remember
that with second degree polynomials, if all else fails, you can always
resort to the
This is a special case of factoring. Any time you have an expression
in the form of
(a + b) (a - b) = a2 - ab + ab - b2Clearly the ab cancels with the -ab, leaving only the a2 and the -b2.
This is useful to know when you have expressions that have square roots in them -- especially when you have square roots in the denominator of some quotient. For example, if you have
4
Ö5 + 1
You can simplify it by multiplying the numerator and the denominator
both by
_ _
4 4(Ö5 - 1) 4(Ö5 - 1)
= = =
Ö5 + 1 (Ö5 + 1)(Ö5 - 1) 5 - 1
_
4(Ö5 - 1) _
= Ö5 - 1
4
Observe that the square root expression is gone from the denominator.
This procedure is called rationalizing the denominator, and it's
useful because square root expressions are easier to deal with when they
occur in the numerator.
You can use this same procedure even if the square root expression contains an unknown, say x. For example:
_____ _____
x x(Öx + 1 + 2) x(Öx + 1 + 2)
= =
Öx + 1 - 2 (x + 1) - 4 x - 3
Again, the right-hand expression is easier to deal with than the left-hand
one. Of course sometimes there are cases where you will want to simplify
the numerator and let the denominator be the form left with the square root
in it. The same method will work:
_____
Öx + 1 - 1 (x + 1) - 1 1
= =
x x(Öx + 1 + 1) Öx + 1 + 1
Notice that we got a cancellation of a factor of x from top
and bottom.
If both Jane and Mary start out at the corner of the barn, and Jane walks 12 meters north, and Mary walks 16 meters west, how far apart are they? Pythagoras pondered this problem over two thousand years ago and came up with a formula that still works today. The key here is that the directions in which Jane and Mary walked are exactly at right angles to each other. This means that the path Jane walked and the path Mary walked are two sides of a right triangle. The third side, or hypotenuse, represents the line that would join them once they have stopped walking.
Pythagoras showed that for any right triangle, the square of the hypotenuse is the sum of the squares of the other two sides. So in the case of Jane and Mary, you have
d2 = 122 + 162 = 144 + 256 = 400To find the distance between Jane and Mary, you need only take the square root of 400. Hence they are separated by 20 meters as the crow flies.
So if you have two points on an x-y graph, one at
d2 = (x2 - x1)2 + (y2 - y1)2And you can find the distance itself by taking the square root of this expression.
You can find a brief biography of Pythagoras by
The idea of a polynomial returning a value based upon some value you put in for x is just a single example of a much more general concept called a function. A function is simply a rule by which if I tell you the identity of some item from group A, you can tell me a unique item in group B that goes with it. For example, if you have a wardrobe of three piece suits, I can point to a pair of trousers, and you can point to the jacket that goes with those trousers. But there can only be one jacket that goes with those particular trousers. Remember, a function has to point me to a unique item in collection B. On the other hand, I can have more than one pair of trousers that goes with the same jacket. That is still a function, because there is no requirement that the item in group A be unique.
The group A of a function is called its domain. That is, the domain is the entire collection of items I might point to. In the suits example, the domain is all the pairs of trousers that are part of your suits. The group B of a function is called its range. That is, the range is all of the items you might point to in response to the ones I might point to. In the suits example, the range is all the suit jackets you own.
Sometimes the domain and the range might be the same. In the same closet where you keep your suits, you also keep your shoes. If I point to one shoe anywhere in your closet, you can point to its mate. That too is a function, but both the domain and the range are all the shoes in your closet.
Mostly calculus is concerned with functions in which both the domain and the range are the real numbers, or at least subsets of the real numbers. So polynomials certainly qualify. If you take a real number x, apply the polynomial, without fail you will get back a real number. So a polynomial is an example of a real valued function of a real variable. The term real valued indicates that its range is the real numbers (or at least a subset of the real numbers). The term of a real variable indicates that its domain is the real numbers (or at least a subset of the real numbers).
Often we will be talking about functions in generalities. We will say,
"a function, f(x)." And that will mean that x is a
variable that can take on any value in the domain of the function, f.
If you have two real valued functions, f and g, then
you can talk about their sum,
One neat thing that happens with real valued functions of a real variable
is that you can take a function of a function.
So, for example, you could take a
real number, x, apply one of the polynomials from the last section
to it, and then apply yet another real valued function of a real variable
to the result. If you have two functions, f(x) and g(x),
then the composite of them is just that, and you can denoted it as
Sometimes when you take the composite of two functions, it
always gives you back the original value you put in. For example,
Substitution of variables: This is something you can do with any function, and you must get comfortable with it before you can be proficient at calculus. The x in the expression, f(x) is what is called a dummy variable. When you say
f(x) = x2 + 3x + 2you are saying that f is a rule you apply to x, no matter what x is. Here is a rule: square x, add to that three times x, and then add two. So, if that is the f rule, then what about
f(a + b) = (a + b)2 + 3(a + b) + 2If you multiply that out, it is the same as
f(a + b) = a2 + 2ab + b2 + 3a + 3b + 2This kind of thing comes up time after time in calculus. It is the method of attack for solving countless calculus problems. So you have no choice but to get the feel of it.
Imagine you are an editor at a children's storybook publisher. Your boss comes to you and says, "The illustrator went and drew lots of pigs for this story. But in the text, the story is about sheep. So go fix the text. Everywhere you see 'sheep' replace it with 'pig'." Not difficult, eh? That's all substitution of variables is. If your boss had told you to replace every sheep in the text with "a pig and a mouse" you could have done that just as easily. So when you have to substitute an expression for a variable into a function, remember that the function is nothing but a storybook text and you are just substituting a particular phrase for some word wherever it occurs.
The Unity of Calculus. In your previous studies, you have already encountered a wide variety of real valued functions of real variables. Besides polynomials there are square roots, nth roots, logs, exponentials, and trig functions (and we will be reviewing logs, exponentials, and trig functions as we encounter them). In calculus, we will be learning a whole new aspect of the lives of these functions. They will all be much in the news. You probably remember each group of functions being taught separately, as if each were a separate garden with fences dividing it from the others. In calculus, you will discover that there are no fences. They are all tied together -- all part of the same perfect garden that is yours to discover if only you keep your eyes wide and don't be afraid to explore under every leaf.