Box 5.2-1: Solution to Exercise 5.2-1

The absolute value function is the prototype function with a cusp. We will be using it later in another problem in order to make it have a cusp as well. Here is a graph of 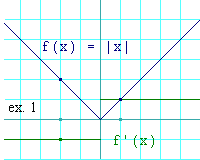 f(x) = |x|, and its derivative. Notice that its derivative, f'(x), is a step function. It is  x = -1  for  x < 0  and  x = 1  for  x > 0. And we can't define f'(x) at all at x = 0. Nowhere is it true that  f'(x) = 0. But it does have a discontinuity that crosses zero at the origin. That is, at  x = 0,  f'(x) goes from -1 to +1. This is what we said earlier is the characteristic of a cusp. And because it is a cusp, we know it has to be a maximum or a minimum.

The rule for determining whether it is a maximum or a minimum is very similar to the rule at stationary points. If the discontinuity in f'(x) is increasing, then the cusp is a minimum. If the discontinuity is decreasing, then the cusp is a maximum. In this case, we can see it is increasing (that is, going from -1 to +1 as x increases) and hence a minimum of f(x).

That takes care of the minimum at the cusp. But the problem, as it is written, also defines end points. It states that we should concern ourselves only with the interval of  -2 £ x £ 1. The endpoints defined by this inequality are -2 and 1. The thing to do is to evaluate the function, f(x), and its derivative, f'(x), at each of the endpoints. Here is a table of what you get:

     f(-2) = 2      f'(-2) = -1

     f(1)  = 1      f'(1)  =  1

Here's the rule for endpoints: On a right-hand endpoint (that is an upper limit on x), if the derivitative is positive there, then the endpoint is a local maximum. If the derivative is negative there, then the endpoint is a local minimum. In this problem, the right-hand endpoint is at  x = 1. Since  f'(1) = 1, which is positive, that means that, by the rule, this point, (-2, 2), is a local maximum.

For a left-hand endpoint (that is a lower limit on x), the rule is just the opposite. If the derivative there is negative, then the endpoint is a local maximum. If the derivative there is positive, then the endpoint is a local minimum. In this problem, the left-hand endpoint is at  x = -2. Since  f'(-2) = -1, which is negative, that means that, by the rule, this point, (1, 1), is a local maximum also.

This still leaves open the problem of what to do if the derivative, f'(x), is zero at an endpoint. It gets a little complicated here. Here is the complete decision tree for deciding endpoints:

                left end                    right end
                   |                           |
                   |     find f'(endpoint)     |
                  /|\                         /|\
                 / | \                       / | \
                /  |  \                     /  |  \
        positive zero negative       positive zero negative
      it's a min   |  it's a max   it's a max  |   it's a min
                   |                           |
                   |    if f'(endpoint) = 0,   |
                   |  take higher derivatives  |
                   |  at the endpoint until    |
                   |  you get one that's not   |
                   |  equal to zero            |
                  / \                         / \
                 /   \                       /   \
                /     \                     /     \
        positive       negative      positive      negative
      it's a min       it's a max        / \       / \
                                        /   \     /   \
                                       /     \   /     \
  derivative number even or odd?    even    odd even   odd
                               it's a min  it's a max  it's a min

And if it is clear that all derivatives are zero at the endpoint, then the endpoint is neither a maximum nor a minimum. For example, a step function, such as the one we discussed here, where  x = -1  for  x < 0  and  x = 1  for  x > 0, has a derivative of zero at all x except at  x = 0, where the function is not defined. In fact, all of its higher derivatives are also zero everywhere except at  x = 0. So any endpoint you might choose for this function would be neither a maximum nor a minimum.

Chances are that you won't have to do any higher-derivative decisions on the exam, but just in case, now you know.

Return to Main Text

email me at hahn@netsrq.com