

Wilbur and Wilma (apologies to any of you whose name matches one of these) are worms. Perhaps you have somebody like them in your life, but that has little to do with the matter at hand. Wilbur the Worm and Wilma the Worm both live in a garden patch planted on a gently sloping hillside. Wilbur has long pined for Wilma's affections, but alas, he is shy and can't bring himself to do more than show off from afar in the wistful hope that she might be watching.
When it comes to showing off, there are advantages to being a worm. Your lithe and slender body can flex in ever so many ways. And one of these just might be the key to Wilma's heart.
It seems that on one particular morning, Wilbur learned that Wilma wears bifocals. And for this reason she sees more clearly what is higher on the sloping garden than what is lower -- at least from a distance.
Wilbur, wishing to show himself in the best way possible, looks at himself and says, "My middle section is looking especially trim today." So he lies on the slope with a bend in his body so that his middle is higher than either his head or tail.
It is on this day that, at last, he catches Wilma's eye. You must understand that she is somewhat bookish, if you'll excuse the suggested pun, and has been busying herself lately with the study of calculus.
"Will you look at that," she says to herself. "The way that handsome
 worm is lying on the slope, his middle forms a maximum of height. If I
follow his length beginning at his head, he slopes up to begin with.
Then right at his maximum height he slopes not at all. Finally, from
just behind his middle all the way to his tail, he slopes back down."
worm is lying on the slope, his middle forms a maximum of height. If I
follow his length beginning at his head, he slopes up to begin with.
Then right at his maximum height he slopes not at all. Finally, from
just behind his middle all the way to his tail, he slopes back down."
She thinks about what she has learned recently. "If l is the length along his lovely body as measured from his nose," she reasons, "then there is a function, h(l) that represents the height of any part of his body. h'(l) would then represent how steeply he increases or decreases in height as I follow his length toward his tail. And just as I've learned, h'(l) is exactly zero at the point on his middle where he is highest."
"But what about where he is lowest? I can't quite make out whether his head is lower than his tail, or vice versa, but at neither of them is h'(l) equal to zero. Yet one of those two is his minimum height. How can that be?"
But then Wilma remembers what she learned about exceptions to the rule. "Yes, I recall. A maximum or minimum can be at a stationary point, where h'(l) is zero, but it can also be at an endpoint where h'(l) need not be zero. Both his head and tail are endpoints so either could be a maximum or minimum. In this case, they are both local minimums, and either one or the other is a global minimum."
At that moment, Wilbur looks up to see Wilma gazing his way. He is at once
startled, nervous, and happier than he has been these many long months.
Of course his change of mood is accompanied by a change of shape.
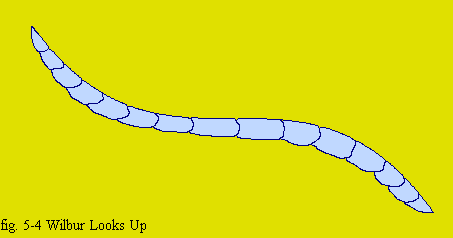
"Oh dear," says Wilma. "His middle is no longer a maximum, nor is it a minimum, local or global. Yet h'(l) is still zero at his middle. So there's a stationary point that is neither a local maximum nor a local minimum. How can that be?"
Wilbur overhears her talking to herself. With great effort, he overcomes his shyness and speaks. "My form never slopes up as you procede from my head to my tail," he assures her. "At my head, it is sloping sharply down. But as you get close to my middle, there is less downward (that is negative) slope. So h'(l) is increasing (that is becoming less negative). That means that h"(l) must be positive near my head. But at my tail, I am sloping down sharply again. That means that from my middle to my tail, my slope must be decreasing (that is growing more negative). So in that half of my body, h"(l) must be negative. But what is h"(l) right at my middle. It appears to be zero."
From Wilma's attentive expression, he gathers that she is fascinated with his explanation. "Stationary points that occur where the second derivative is negative," he continues, "are maximums, and stationary points that occur where the second derivative is positive are minimums. That is the rule. If the second derivative is exactly zero at the stationary point then (usually) the stationary point is neither a maximum nor a minimum [I'll cover the exception to this rule after the end of this story]. Such stationary points are said to be inflection points as well." [note that "inflection" is sometimes spelled "inflexion," which is the British spelling]
 "So pleasant to meet a gentleman who is well versed in a topic that
interests me," she says. "Then you too dabble in calculus and hence must
understand the subtlies of inflection points. Please tell me more."
"So pleasant to meet a gentleman who is well versed in a topic that
interests me," she says. "Then you too dabble in calculus and hence must
understand the subtlies of inflection points. Please tell me more."
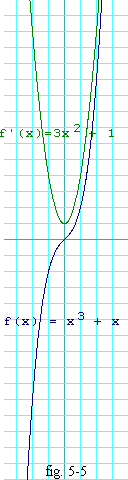
"I'm sure your knowledge surpasses mine by as much as your beauty surpasses mine," Wilbur begins. "Recall that the second derivative of a function, f(x), is the dervative of its derivative. Recall also that a stationary point of f(x) is where f'(x) is zero. Well, an inflection point is where f'(x) has a stationary point and where f'(x) is either at a local maximum or a local minimum of its own. That means that at an inflection point, f"(x) must be zero. When an inflection point coincides with a stationary point, that stationary point becomes an exception to the rule. It can be neither a local maximum nor a local minimum."
"I see," says Wilma. "Inflection points of a function do not necessarily have
to be at its stationary points. For example, the function,
"But observe this," says Wilbur, drawing a graph of Wilma's functions in
the sand. Notice that
"Sir!" replies Wilma. "All this wonderful talk of calculus and squiggles is making me feel so warm and flushed. You wouldn't be trying to take advantage of me, would you?"
Even a shy worm like Wilbur can recognize his cue when he hears it. With
that, he slips off her bifocals, takes her in his non-arms, and kisses her.
 When their lips part and Wilma has caught her breath, she says, "How very
strange. Look carefully at our maximum height when we kiss ..."
When their lips part and Wilma has caught her breath, she says, "How very
strange. Look carefully at our maximum height when we kiss ..."
This time, she kisses him.
"Our height has a maximum," she says, "at the point we were joined. Yet there is no stationary point there. How can that be?"
"How can there be a stationary point where we join in passion?" says Wilbur. "You can't even define h'(l) at that point."
"Why not?" asks Wilma.
"From left to right, the slope is sharply up on your side and sharply down on my side. Our derivative is discontinuous where we joined. That is the last exception to the rules. A local maximum or minimum must be a stationary point (and one that is not also an inflection point), an endpoint, or a point at which the derivative is discontinuous. For the last case, the derivative must in fact pass through zero discontinuously. Some folks call points like that cusps. You can recognize cusps on a graph because the trace appears to turn a corner all at once there."
"This has cast light on ever so many questions I have had, sir," says Wilma. "Perhaps we can go some place cozy and discuss higher derivatives at greater length."
As promised, I will give you the true test for inflection points shortly.
First, consider that we defined the second derivative of a function as
the derivative of its derivative. Is there any reason we need to stop
there? Can't the second derivative of a function also have a derivative
of its own? And wouldn't the natural name for the derivative of the second
derivative be the third derivative? In fact, couldn't you keep
taking further derivatives and come up with the fourth, fifth, sixth
derivatives -- or even the nth derivative for any positive integer
n? For example, the function that interested Wilbur and Wilma
was
f'(x) = 3x2 + 1 f"(x) = 6x f(3)(x) = 6 f(4)(x) = 0 f(5)(x) = 0
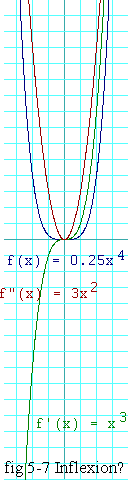 In fact all the derivatives, fourth and upward, are zero. Note the notation
for derivatives of order higher than second. Some books use this notation,
others use a superscripted Roman numeral (e.g.
fiv(x) indicates fourth derivative).
Both notations mean the same thing.
In fact all the derivatives, fourth and upward, are zero. Note the notation
for derivatives of order higher than second. Some books use this notation,
others use a superscripted Roman numeral (e.g.
fiv(x) indicates fourth derivative).
Both notations mean the same thing.
Now we can begin discussion of when something is an inflection point.
The first rule is that in order for a to be an inflection point
of f(x), it must be a stationary point of f'(x).
That means, as we already know, that
Remember how Wilbur said that an inflection point is where a function's
derivative has a maximum or a minimum. If f(x) is the function
we are examining for inflextion points, then let
So, can a function have its second derivative be zero at some point yet
not have an inflection point there? Figure 5-7 shows an example of just
that. The blue trace is the function,
If we let
Here is the rule: If f(x) is a function that has higher derivatives,
then if
But if f(3)(a) is zero, then what? It still might
be an inflection point. To determine if it is, keep taking higher derivatives
until you come up with one that is nonzero at
In the case we have been examining,
The exceptions to maximums and minimums being at stationary points are:
a) That a maximum or minimum can be at an end point. If you are
only concerned with
b) That a function's maximum or minimum can be at a point where its derivative is discontinuous. We called such points cusps.
c) That a stationary point is not a maximum or minimum if it is also an inflection point. But if a stationary point is not also an inflection point, then it must be either a local maximum or local minimum.
d) If a function's second derivative is zero at some point, then
you can use the odd-even rule of higher derivatives to determine whether
or not that point is an inflection point. That leaves only one question.
If you have a stationary point at
In the case of
Your curriculum may not cover the odd-even rule, but it will certainly cover
all the rest that we have covered in this section. You should be prepared
to answer an exam question phrased as: Find all the maximums, minimums,
stationary points, and inflection points of the function
1) Find local maximums and minimums for
2) Find local maximums and minimums for
3) Find local maximums and minimums for
4) Find local maximums and minimums for
5) Find local maximums and minimums for
6) Find local maximums, minimums, and inflection points for
4x
f(x) =
1 + x2
Note that you will need to use both the
quotient rule and the
chain rule to do this problem.
Move on to 5.3 The Way to Shangrila
email me at hahn@netsrq.com