Box 5.2-2: Solution to Exercise 5.2-2

This problem is merely a test of your ability to deal with endpoints. Here is a graph of 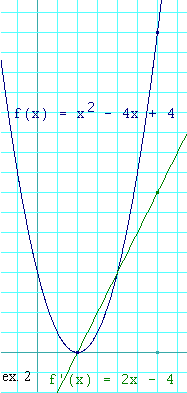 f(x) = x² - 4x + 4, and its derivative,  f'(x) = 2x - 4. The left-hand endpoint is at  x = 2. The right-hand endpoint is at  x = 6. We can see that f'(x) has no discontinuities, so there ought not be any cusps in this function.

If we make a table of the values of f(x) and f'(x) at the endpoints, we get:

     f(2) = 0       f'(2) = 0

     f(6) = 16      f'(6) = 8

Here again is the decision tree for deciding whether endpoints are maximums or minimums:

                left end                    right end
                   |                           |
                   |     find f'(endpoint)     |
                  /|\                         /|\
                 / | \                       / | \
                /  |  \                     /  |  \
        positive zero negative       positive zero negative
      it's a min   |  it's a max   it's a max  |   it's a min
                   |                           |
                   |    if f'(endpoint) = 0,   |
                   |  take higher derivatives  |
                   |  at the endpoint until    |
                   |  you get one that's not   |
                   |  equal to zero            |
                  / \                         / \
                 /   \                       /   \
                /     \                     /     \
        positive       negative      positive      negative
      it's a min       it's a max        / \       / \
                                        /   \     /   \
                                       /     \   /     \
  derivative number even or odd?    even    odd even   odd
                               it's a min  it's a max  it's a min

Note that our left-hand endpoint yields zero for its derivative. According to the decision tree, we take the next higher derivative until we get a nonzero value. In this case,  f"(x) = 2, which is nonzero everywhere. That means that the second derivative at the left-hand endpoint is positive. The decision tree tells us that this endpoint, (2, 0), is a minimum.

The right-hand endpoint is no problem. We see that  f'(6) = 8, which is positive. The decision tree tells us that this endpoint, (6, 8), a maximum.

Return to Main Text

email me at hahn@netsrq.com