Karl's Calculus Tutor - Solution to Exercise 7.2-6

Solution to Exercise 7.2-6

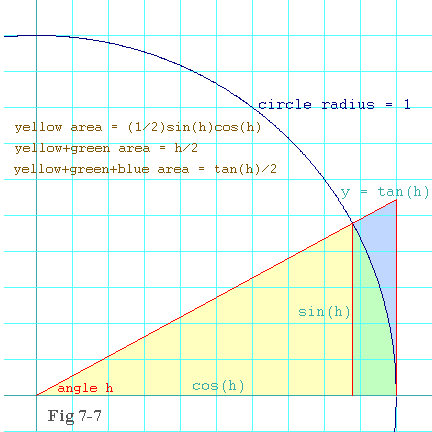
This first part of this is easy because I practically gave it away with the hint. If you join the point, (cos(h),sin(h)), and the point, (1,0), with a new line segment, you form a triangle whose base is 1 and whose height is sin(h). Hence its area is sin(h)/2. We already saw that the area of the pie-slice (that is the combined green and yellow areas) is h/2. And you can see that the new triangle is entirely contained inside the pie-slice. So the area of the new triangle must be less than the area of the pie-slice. Therefore it must be true that sin(h)/2 < h/2, and consequently sin(h) < h.

The second part was to do a delta-epsilon proof that f(x) = sin(x) is continuous at x = 0. You will recall from the section on continuity that for f(x) to be continuous at x = 0, then it must be true that

    lim    f(x)  =  f(0)
   x  > 0

In this case f(0) = sin(0) = 0. So you must do a delta-epsilon proof that

   lim    sin(x)  =  0
  x  > 0

The delta-epsilon contract here is that for any e > 0 I might name, no matter how small, you will be able to name a d > 0 that makes it always the case that

   |sin(x) - 0|  £  e

or equivalently

   |sin(x)|  £  e

whenever |x| £ d. So the problem is to name a d that will make this contract will be met.

But above we just proved that when x is in the first quadrant, sin(x) < x. And because sin(x) is an odd function (that is sin(-x) = -sin(x) ), you can extend that inequality to

   |sin(x)|  <  |x|

whenever x is in the first or fourth quadrant. And since x is supposed to be close to zero in this problem, we can certainly make that restriction. Combining this inequality with the delta-inequality we have

   |sin(x)|  <  |x|    £    d

You can stick this into your epsilon-inequality to get

   |sin(x)|  <  |x|    £     d     £     e

In other words, if you choose your d small enough to guarantee |x| £ e, and since |sin(x)| < |x|, by doing so you have guaranteed that |sin(x)| < e.

That means that you need only choose your d to be anything greater than zero and less than or equal to whatever e I have named, and you will satisfy the contract.

And since we've shown that sin(x) is equal to its limit at x = 0, we have proved that sin(x) is continuous at x = 0.

Return to Main Text

email me at hahn@netsrq.com