

Let's get right back to the train that circles around New Atlantis. When the train is parked at Main Street and 10th Avenue East, it faces due north. Suppose it rolled 0.1 km counterclockwise from that stop. How far north would it be. We already know from our discussion in the last section that it would be sin(0.1) km north of the intersection at Main Street and 10th Avenue East. But look carefully at the diagram. As the train rolls out from the station, isn't it going almost due north. Indeed, during that entire 0.1 km of track isn't it going pretty close to north the whole way?
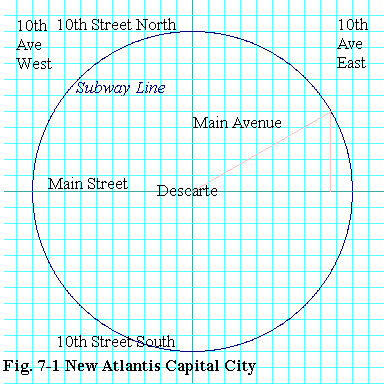
And so, for each meter of track the train covers in that first 0.1 km, doesn't it go almost a meter north? Another way of saying this would be to say that sin(0.1)/0.1 is very nearly equal to one. My calculator gives 0.998334166 as the value of that expression carried out to 9 figures. That's pretty close to one.
Still, you have to agree that even in that first 0.1 km, the track does diverge slightly from due north. If you eyeball the diagram carefully you can even see it. But in the first 0.01 km, it diverges from due north even less. If you look at the diagram, in the first tenth of a block, you can't even discern any curvature of the track. It's extremely close to pointing due north the whole way. So if in the first 0.1 km the train was very nearly going one meter north for every meter around the track, in the first 0.01 km, it should be even more nearly going one meter north for every meter around the track. In other words, sin(0.01)/0.01 ought to be closer to one than sin(0.1)/0.1 was. And indeed, my calculator gives 0.999983333 for the value of sin(0.01)/0.01. That's a whole lot closer to one than sin(0.1)/0.1 was, and it was pretty close to begin with.
As you try shorter and shorter lengths of track from the station at Main Street and 10th Avenue East, our sense of geometry tells us that the the train will be going closer and closer to due north the entire way. If h is the length of track traveled from the station, then it seems that as h gets shorter and shorter, sin(h)/h should get closer and closer to one. To put this in mathematical terms, we have a sense that
sin(h)
lim = 1 eq. 7.2-1
h > 0 h
But you should know by now that just having a sense of something is never
enough in mathematics. To be sure of anything, you always need proof.
And so we will now prove that equation 7.2-1 is true. Follow along carefully
because this may be on an exam.
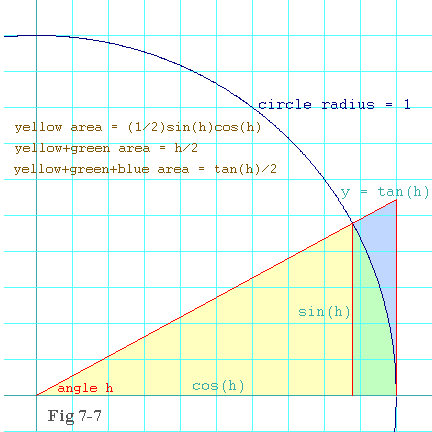
Look at figure 7-7. You can see a small right triangle inscribed
in the circle whose interior is shaded yellow. The radius of the
circle is one again. The angle at the
center is h so the base of this triangle is cos(h)
and the height is sin(h). According to the formula you already
know for the area of a triangle (
The circumscribed right triangle (that's the big one) that comprises
the yellow, the green, and the blue shading, has a base equal to the
radius of the circle, which is one, and a height of tan(h)
(
But what about the area comprising just the yellow and the green shading? It is a pie-slice, and therefore represents the same fraction of the area of the entire circle that the angle, h, is of the entire circumference. In other words, because h is not only the angle in radians, but also the distance around the circumference subtended by that angle, it follows that h is to 2p radians as the area in question is to the area of the circle.
Once again, the radius of the circle is unity, so according the formula
for the area of a circle (
h a
= eq. 7.2-2
2p p
The p's cancel, and
hence the yellow-plus-green area must be exactly h/2.
Now observe that the yellow-plus-green-plus blue area must be greater than the yellow-plus-green area, which in turn must be greater than the yellow area alone. In math symbols, that means
tan(h) h sin(h)cos(h)Now cancel the 2's and divide through by sin(h) (notice that sin(h) is positive, so we can divide the inequality by it. If you divided by a negative quantity, you would have to reverse the direction of the inequality signs). Since>>eq. 7.2-3 2 2 2
1 h
> > cos(h) eq. 7.2-4
cos(h) sin(h)
Remember that when cos(h) is positive, it is
always less than or equal to one, so
1/cos(h) is always greater than or equal to one.
And cos(h) is always positive when h is
small. In fact, as h gets closer and closer to zero,
cos(h) gets closer and closer to one. And, of course,
so does 1/cos(h), but from the other direction.
When you take the limit as h goes to zero, you find that h/sin(h) is being squeezed between something just greater than one and something just less than one. And as h goes to zero, both the rock and the hard place close in on exactly one (this technique of trapping a limit between two things that approach each other is, in fact, called the squeeze theorem or the squeeze method). So h/sin(h) must be squeezed to that limit as well. And we conclude that
h
lim = 1 eq. 7.2-5a
h > 0 sin(h)
It follows immediately that
sin(h)
lim
|
as well.
Recall that the train travels aournd the track at 1 km per minute. Suppose nobody wants to get on or off the train at Main Street and 10th Avenue East. So the train doesn't bother to stop there -- it rolls right through the station at 1 km per minute. So what is its northward speed at that exact moment? Since the train is pointed due north at that moment, our intuition tells us that its northward speed must also be 1 km per minute as well. But now think of it in calculus terms. Remember that speed is the derivative of position with respect to time. If x(t) is the trains east-west position as a function of time and y(t) is its north-south position as a function of time, then the northward speed when the train rolls through the station will be y'(t) at the moment, t, that it is at the station.
Let's call the moment that the train passes the station,
y(h) - y(0)
y'(0) = lim eq. 7.2-6
h > 0 h
Now look at the diagram of the track once more. Can you see that
as the train circles the track at 1 km per minute, its
position at any time will be
dsin(t) sin(t+h) - sin(t)
y'(t) = = lim eq. 7.2-7
dt h > 0 h
When you put in zero for t, equation 7.2-7 becomes easy because
sin(h)
y'(0) = lim = 1 eq. 7.2-8
h > 0 h
That confirms that the northward speed of the train as it rolls through
the station is exactly 1 km per minute. But what about its
northward speed at some other time besides
sin(t)cos(h) + sin(h)cos(t) - sin(t)
y'(t) = lim eq. 7.2-9a
h > 0 h
Breaking this up into three fractions, you get
sin(t)cos(h) sin(h)cos(t) sin(t)
y'(t) = lim + - eq. 7.2-9b
h > 0 h h h
Now observe that as h goes to zero, cos(h) goes to
one. And that means that the first and third terms of the limit cancel,
and you're left with
sin(h)cos(t)
y'(t) = lim eq. 7.2-9c
h > 0 h
Furthermore, the sin(h)/h goes to one as h goes to zero.
And that leaves you with just
y'(t) = cos(t) eq. 7.2-9d |
That's it. The derivative of the sine is the cosine. Look carefully
 at the graph of sine and cosine and try to see how the slope of the
sine trace (in blue) is always exactly equal to the cosine trace
(in green).
at the graph of sine and cosine and try to see how the slope of the
sine trace (in blue) is always exactly equal to the cosine trace
(in green).
And what about the train's east-west speed at any time, t?
Remember that the east-west position of the train is given by
cos(t+h) - cos(t)
x'(t) = lim eq. 7.2-10a
h > 0 h
Again a
cos(t)cos(h) - sin(t)sin(h) - cos(t)
x'(t) = lim eq. 7.2-10b
h > 0 h
Again, as h goes to zero, cos(h) goes to one. And that
makes the first and third terms in the limit cancel.
-sin(t)sin(h)
x'(t) = lim eq. 7.2-10c
x > 0 h
And again, sin(h)/h goes to one as h goes to zero, so
x'(t) = -sin(t) eq. 7.2-10d |
And you're left with the derivative of the cosine is minus the sine. I urge you to study the graph in figure 7-3 again and see how the sine trace (in blue) is always the opposite of the slope of the cosine trace (in green).
In the trig identity section,
you learned that these four functions were merely quotients of the
sine and cosine functions. So to find the derivatives of
tan, cot, sec, and csc, it would make sense to
use the quotient rule. Let's begin
by finding the derivative of
sin(x)
f(x) = tan(x) = eq. 7.2-11a
cos(x)
Remembering that the derivative of the sine is the cosine and
the derivative of the cosine is minus the sine,
we apply the quotient rule to the quotient on the right to get:
cos(x)cos(x) - sin(x)(-sin(x))
f'(x) = eq. 7.2-11b
cos2(x)
or equivalently:
cos2(x) + sin2(x)
f'(x) = eq. 7.2-11c
cos2(x)
You can simplify equation 7.2-11c in two different ways. One is to recognize
the trig identity that you have in the numerator, namely that sine squared
plus cosine squared of the same quantity is always equal to 1.
That leaves you with the reciprocal of cos2(x), which
is the same as sec2(x).
The other simplification is to observe that the left-hand summand in the
numerator is identical to the denominator. So if you break it up into
the sum of two quotients, the left-hand quotient will be 1, and
the right-hand quotient will be tan2(x).
Hence, here are the two simplifications:
1
f'(x) =
|
The two forms (equation 7.2-11d and 7.2-11e) are identities of each other, and therefore entirely equivalent. So the derivative of the tangent is the secant squared. But it is also true that the derivative of the tangent is one plus the tangent squared. The latter is a very important property of the tangent function (that is to take its derivative you simply square it and add 1), and we will make use of it later on.
If you recall that cot(x) is simply the reciprocal of the tangent, you should be able to apply the same attack on it as we did above on the tangent function to show that the derivative of the cotangent is minus the cosecant squared, and that equivalently the derivative of the cotangent is minus one minus the cotangent squared. I urge you to take out pencil and paper right now and do this as an exercise.
Finding the derivative of secant and cosecant is even easier than
doing so for tangent and cotangent. You can use the
quotient rule if you like, or you can
observe that the derivative of
-1
h'(x) = f'(g(x)) g'(x) =
|
So the derivative of the secant is the tangent times the secant. Once again, as an exercise, I urge you right now to use the same attack to show that the derivative of the cosecant is minus the cotangent times the cosecant.
One way of finding the derivative of
y = arcsin(x) eq. 7.2-13would be to apply
dy arcsin(x + h) - arcsin(x)then use identities and tricks and algebra to work it through. Don't try it. They won't ask you to do that on any exam. The easy way to work this derivative is to use the= limeq. 7.2-14 dx h> 0 h
sin(y) = x eq. 7.2-15Now take the derivative of both sides, applying the chain rule to the left-hand side.
cos(y) y' = 1 eq. 7.2-16But by the trig identity that you've memorized by now, you know that
sin2(y) + cos2(y) = 1 eq. 7.2-17or equivalently
___________
cos(y) = Ö1 - sin2(y) eq. 7.2-18
And because equation 7.2-13 tells you that
______
cos(y) = Ö1 - x2 eq. 7.2-19
And you can substitute that expression for cos(y) back into
equation 7.2-14 to get
______
Ö1 - x2 y' = 1 eq. 7.2-20
That makes it pretty easy to solve for y'.
1
y' =
|
And that is the derivative of arcsin(x). Go over it several times, since they might pop this derivation on you on the exam.
Interesting, isn't it, how a simple algebraic function made only from squares and square roots can be the derivative of something as abstract as an inverse trig function. What's happening here is that this derivative is telling us something about the relationship of sin(x) to its derivative. Think about it. Taking the derivative of sin(x) is equivalent to squaring it, subtracting the result from 1, then taking the square root of that. Of course, that doesn't work for any function. But for sin(x) it does. It's a special relationship that sin(x) enjoys with its own derivative. The concept of a function's derivative being related to the function itself according to some algebraic rule is an important one that you will be coming back to when you get to more advanced material. For now, just make a mental note of it and move on. And if the though tickles your fancy, all the better.
1) Use what you learned above about a) the derivative of the
tangent function, and b) taking the derivative of an inverse function
to determine the derivative of
2) Use the
product rule to determine the
derivative of
3) Use the product rule and the chain rule to find the derivative of
f(x) = x sin( 1/x )What can you say about f'(x) when
4) Use implicit differentiation on each of the following (where y is a function of x in each case):
a) sin(y) = cos(x2) b) y tan(x) = x c) sin(xy)cos(x) = y2 d) tan2(y) = cos(2x)Click here to view solutions, but try to do them all before you do.
5) Find the limit:
1 - cos(h)
lim
h > 0 h2
Hint: Use the
difference of squares
and a common trig identity to convert this into limit having to
do with sin(h). Then use what you know about the
limit as h goes to zero of sin(h)/h. When you
are done, |
6)
Use figure 7-7 (shown here again for your convenience) to prove that
for positive h in the first quadrant, it is always true that
|

|
In the last exercise above you proved that
The outline of the proof is that first we set up the delta-epsilon contract that we have to meet for
lim sin(x) = sin(c) eq. 7.2-22
x > c
to be true for all x. Recall that this is the limit that
defines continuity.
We will make a change of variables that puts the d term to work invisibly inside the contract expression. You will see that once we set up the delta-epsilon contract in this way, there will be a trig identity that we can apply right away. We will then show that each of the terms in the resulting expression is less than some very simple expression. By combining the simple expressions, we will have an easy way to quantify the d in terms of e so that the contract must be met.
But first, some more basic inequalities concerning sine and cosine.
You recall that for
cos2(h) £ |cos(h)| eq. 7.2-23a 1 - |cos(h)| £ 1 - cos2(h) = sin2(h) < h2 eq. 7.2-23bor more succinctly,
1 - |cos(h)| < h2 eq. 7.2-23cAlso please recall from algebra that for any a and b, it is always true that
One last note. This may seem obvious, but it bears repeating before getting
into the meat of this proof. And that is that the relation, <,
is transitive. So is the relation,
£. That means, for example,
that if
Step 1: Write the contract. To prove the limit shown in
equation 7.2-22, the contract is that whatever
|sin(x) - sin(c)| < e eq. 7.2-24whenever
Step 2: A change of variable. Observe that if
|sin(c ± h) - sin(c)| < e eq. 7.2-25
Step 3: Apply the identity for the sine of a sum (or difference).
You remember,
|sin(c)cos(h) ± sin(h)cos(c) - sin(c)| < e eq. 7.2-26aYou can combine the first and third terms that are inside the absolute value sign to get
|sin(c)(cos(h) - 1) ± sin(h)cos(c)| < e eq. 7.2-26b
Step 4: Use the absolute value inequality. If
|sin(c)(cos(h) - 1)| + |sin(h)cos(c)| < e eq. 7.2-27athat would guarantee our contract. Notice that
|sin(c)(1 - cos(h))| + |sin(h)cos(c)| < e eq. 7.2-27bis the same thing.
Step 5: Restrict the range of h.
This is the same as restricting the range of
d. But the contract allows us to
make d as close to zero as we like.
So there is no problem restricting it to
Step 6: Substitute simpler terms that are known to be greater.
Once again, if something greater than our contract expression is less
than e, then that forces the
contract expression to be less than e as well
(because of transitivity).
So, for example, we know that if
|sin(c)h2| + |sin(h)cos(c)| < e eq. 7.2-28aLikewise, since
|sin(c)h2| + |h cos(c)| < e eq. 7.2-28bstill guarantees the contract. We also know that no matter what c is,
|h2| + |h| < e eq. 7.2-28cAnd since h is positive, this becomes simply
h2 + h < e eq. 7.2-28dAt this point, we could just go and solve the quadratic inequality above. But there is an easier way. Remember that
h + h = 2h < e eq. 7.2-28eor equivalently
h < e/2 eq. 7.2-28fIf you can choose h so that it satisfies this inequality, this still guarantees the contract.
Step 7: Bring back the d.
Since
And that is the proof that sin(x) is continuous. Admittedly it's a lot to swallow all at once. But go back and reread the outline of the proof up at the beginning. Then see how each step works into something in the outline. The outline tells you through which towns the proof passes. The detailed steps tell you where to make your right and left turns so that you end up unerringly at your destination. If you think about complicated proofs that way, you will never get lost.
Move on to The Cheshire Cat's Grin (L'Hopital's Rule)
email me at hahn@netsrq.com