Solution to Exercise 8.2-6

The problem was: Actor, Tyrone Olivier, is exactly 6 feet tall. He delivers a soliloquy on stage, illuminated only by a single footlight, which is at the same level as the floor of the stage. 24 feet behind the footlight is the vertical backdrop of the stage. He begins walking toward the footlight at 2 feet per second. When he is 8 feet from the footlight, at what rate is his shadow on the backdrop increasing in height? The hint was to make a diagram and use similar triangles.

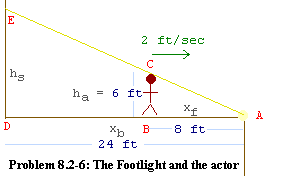
Here's the diagram. Observe that triangle ABC is similar to triangle ADE. This means that the ratio of lengths, AB:BC is the same as the ratio of lengths AD:DE. Note also that the lengths of AB, BC, and AD are all given in the problem (although length AB does vary with time). With that in mind, let's go and answer the seven questions.

Answering question 1, we can see that the problem asks for a rate (in time) at which the actor's shadow is growing. So the independent variable is again time, t.

Answering question 2, since the problem asks for the rate at which the shadow height is growing, shadow height, h_s, seems an obvious candidate as a dependent variable. That height is the same as length DE. And since the problem talks about his walking toward the footlight, his distance from the footlight, x_f, also seems an obvious candidate. That distances is the same as length AB. Note that the height of the actor, h_a, and the distance from the footlight to the backdrop, x_b, are both constants. These correspond to lengths BC and AD respectively.

Answering question 3, there are no inferred variables in this problem. The dependent variables you came up with answering question 2 covers everything there is about this problem.

Answering question 4, the relationship between the two dependent variables, x_f and h_s, are determined by having similar triangles. A little while back you saw that the ratio, AB:BC, had to be the same as the ratio, AD:DE. Isn't this the same as the equation,

   xf     xb
       =                                                          eq. p6.1
   ha     hs

Question 5 tells you to take the derivative with respect to the independent variable of whatever relationship(s) you came up with when you answered question 4. Note that in equation p6.1, the symbols, x_b and h_a are both constants (the backdrop does not get any nearer or farther from the footlight, and the actor himself does not grow or shrink). Only x_f and h_s are functions of the independent variable, t. So they are the only ones you take derivatives of. You must treat the constants as scalars (that is they are just along for the ride).

    1 dxf        xb dhs
           =  -                                                   eq. p6.2
   ha  dt       hs2  dt

Question 6 tells you to solve for whatever the problem is asking for. In this case it is asking for the shadow height the rate at which the shadow grows, which is dh_s/dt.

      hs2  dxf     dhs
   -            =                                                 eq. p6.3
     ha xb  dt      dt

Question 7 tells you to put in the numbers the problem gives you. These are  x_f = 8 ft,  h_a = 6 ft, and  x_b = 24 ft for distances. The problem also tells you that the actor is moving toward the footlight at 2 ft/sec. This means that x_f is decreasing at that rate. So you know that  dx_f/dt = -2 ft/sec (make sure you see why this derivative is negative). Plugging all this into equation p6.3 gives

     hs2          hs2     dhs
   -     (-2)  =       =                                          eq. p6.4
     144           72      dt

          xb        24
   hs  =     ha  =     × 6  =  18 ft                              eq. p6.5
          xf         8

   dhs     182     324
        =       =       =  4.5 ft/sec                             eq. p6.6
    dt      72      72

Return to Main Text

email me at hahn@netsrq.com