Section 8: More Tricks with DerivativesKCT logo

© 1999 by Karl Hahn

8.2 The Dance of the Derivatives: Related Rates

A Shaggy Dog Story

That little doggie looked so cute when you first brought him home. How could any creature so adorable make such a mess of your house? Here is his latest (though by far not his messiest) caper. It seems he has discovered the bathroom. And in it is this wonderful toy hanging on the wall with a soft end dangling down that is just begging to be pulled. Which is what he is now in the habit of doing. He trots into the bathroom, grabs the end of the toilet paper, and then runs out the door with a streamer unreeling behind him.

With all this happening, amazingly you are thinking about calculus and asking yourself, "If the dog runs at 2 meters per second, how quickly is the radius of the toilet paper roll decreasing?" Of course you are.

Before we dive into the how to of this problem, we need a little more information. One is how thick is the toilet paper. Why do we need to know this? Well if the paper were very thick then we'd expect that each turn of the roll would reduce the radius by more than if the paper were thin. We'll say that this particular brand is 0.00005 meters thick (that's about 2 mils in the English system of measures). Also since the radius of the roll is changing at a rate which is perhaps not constant, we need the problem to state at exactly what moment we want to know this rate of change. So let's say it is at the moment when the radius of the roll is 0.05 meters (about 2 inches).

The first trick in this problem is to relate the radius of the roll to how much toilet paper the dog has already pulled off. Visualize the roll in crossection. It has a crossectional area of A = pr2, where A is area and r is radius. I could, at this point, substitute 0.05 meters for r, but usually it is good practice to wait until the end of the problem before you substitute values for variables. So that's what we'll do.

Now consider the thickness of the toilet paper, x (which the problem stated was equal to 0.00005 meters), and think about how much area a length, s, of toilet paper of that thickness contributes to the crossectional area of the roll. If you look at that piece of toilet paper edge on, it is a very long and thin rectangle. And the area of that rectangle is thickness times length, or xs.

The rate at which the dog pulls toilet paper off the roll is given in the problem. And that rate is the time derivative (where t is the time variable) of the length of paper he has already pulled. 

   ds
       =  2 meters/sec                                            eq. 8.2-1
   dt
Do you see what that equation is saying? The rate at which length of paper, s, is being pulled off the role with respect to time, t, is 2 meters per second.

With each meter of paper the dog pulls off, the crossectional area of the roll is reduced by x times one meter. The rate at which he pulls the paper off is given in eq. 8.2-1 in meters per second. So the equation for how fast the crossectional area of the roll is reduced is 

   dA        ds
       =  -x                                                      eq. 8.2-2
   dt        dt
What this equation says is that the crossectional area of the roll, A, is reduced (that's where the minus sign comes from), and the rate with respect to time, t, that it is reduced is the paper's thickness, x, times the rate it is being pulled off, ds/dt, in meters per second. Note that dA/dt has units of square meters per second.

But how is all this crossectional area stuff related to the radius of the roll? The crossection of the roll is a circle. So we get this relationship from how the area of a circle is related to its radius. 

   A  =  pr2                                                      eq. 8.2-3a
But both A and r are functions of time, t. That is, it would be reasonable to express them as A(t) and r(t) respecively. So another more explicit way to write this is 
   A(t)  =  pr2(t)                                                eq. 8.2-3b
Now look at what happens when you take the time derivative of both sides of equation 8.2-3b. Clearly on the left we get dA/dt. On the right, though, we have a function of a function -- that is a composite. It is a composite of the radius function of time, r(t), and the function of squaring the radius. So we have to apply the chain rule.

The derivative of squaring the radius is 2r(t). And the derivative of the radius function itself, r(t), is dr/dt. So the derivative of the radius function squared is 2r(t) dr/dt. That gives us, for the entire equation of the derivative of equation 8.2-3b: 

   dA            dr
       =  2pr(t)                                                  eq. 8.2-4
   dt            dt
Observe what the problem asks for. It is asking for the rate at which the radius of the roll decreases. Isn't that dr/dt? So we need to solve for that: 
   dA  1    1      dr
                =                                                 eq. 8.2-5a
   dt  2p  r(t)     dt
We already have an expression for dA/dt from equation 8.2-2. So we substitute that in for dA/dt. 
      ds  1    1      dr
   -x               =                                              eq. 8.2-5b
      dt  2p  r(t)     dt
And now it all works out because ds/dt, x, and r(t) are given in the problem. Remember 
   ds
         =  2 meters/second
   dt

   r(t)  =  0.05 meters

   x      =  0.00005 meters
So finishing the solution is just a matter of plugging in values. My calculator tells me that 
   dr
       =  -0.0003183 meters/second                                eq. 8.2-5c
   dt
which is about -0.012 inches per second. Observe that the result is negative. This indicates that the radius of the roll is decreasing with time, as we would expect.

Seeing that the sign of the result is as you would expect it is just one of the things you can do to check your solution for correctness. Here are some others:

  1. If you increase the thickness, x, of the paper, do you expect that the roll will shrink faster or slower? It would shrink faster because each turn of the roll takes off more area from the crossection of the roll. Now look at equation 8.2-5b. Does it predict that increasing the thickness makes the roll shrink faster?
  2. If the dog runs faster, that is if you increase ds/dt, do you expect the roll to shrink faster or slower? Faster of course. Does equation 8.2-5b predict that?
  3. If the radius, r(t), is smaller, do we expect the roll to shrink faster or slower? Think about this one. With a smaller radius it's circumference is less, so with each meter of paper pulled you will get more turns of the roll. So the roll shrinks faster when it is smaller. Does the way r(t) appears in equation 8.2-5b predict this?

Perhaps you have not been in the habit of doing checks like the ones I have shown above. Now is a good time to start. You will save yourself a lot of wrong answers by performing reasonableness checks on all your solutions to problems, especially if you are headed into engineering or the sciences. Remember that if someday you are solving problems as part of your profession, there will be no answers in the back of the book for you to check against. You will have to know whether or not your answer is right on your own.

The Seven Veils: The Questions to Ask Yourself When Doing Related Rates Problems

Question 1: What is the independent variable in this problem? The independent variable is usually (but not always) time, which you traditionally notate using the symbol, t. The key phrases that indicate time to be the independent variable are "how fast," "how often," "at what speed," "at what rate is this or that changing," and so on. In rare cases a related rate problem might have something other than time as its independent variable. If, for example, the problem asks "how much water boils for each gallon of fuel," you can be relatively sure that the independent variable is gallons of fuel. The word, "per," or the phrase, "for each," gives you a clue that the word or phrase that follows is likely to be an independent variable.

Question 2: What dependent variables does the problem reveal? In the case of the doggie problem above, radius of the roll is clearly a dependent variable, since the problem asks you about it. Anything that the problem mentions that is a function of the independent variable you arrived at by asking yourself the first question is probably going to be a dependent variable. Since the problem mentions the length of paper being pulled (or at least the rate of length of paper being pulled) that means that length of paper being pulled is also a dependent variable.

Question 3: What other dependent variables (if any) does the problem imply? For this you have to use your own knowledge of how the world works. Often this is not an easy question to answer. In the case of the doggie problem, the implied dependent variable was the crossectional area of the roll. We were only able to arrive at this by thinking carefully about what happens when you pull paper off a roll. In other problems you will have to use your knowledge of geometry or trig to answer this question. But answering it always starts with taking a moment to clearly visualize what is going on in the problem. And quite often, the problem will indeed state all the variables you need in order to solve it, in which case the answer to this question will be none.

Question 4: What are the relationships between the variables? Again this often involves tapping your world knowledge as well as what you learned in geometry and trig. In the doggie problem, we have real-world knowledge that toilet paper rolls usually have a circular crossection. And we know from junior high school that the area of a circle is pr2. That gives us the relationship between dependent variable, radius, and dependent variable, area.

Question 5: What do you get when you take the derivative with respect to the independent variable of both sides of the relationship equation(s)? This just means you have to take some derivatives. You will almost always have to apply the chain rule, because one of your dependent variables will very likely be squared or cubed or square rooted, or have some trig function taken of it. Here are some examples using t as the independent variable:

  1. If you have dependent variable, y, and you see the expression, y3 - y, then the derivative of that expression is: 
                 dy
   (3y2 - 1)   
             dt
  2. If you have dependent variable, q, and you see the expression, sin(q), then the derivative of that expression is: 
              dq
   cos(q)   
          dt
  3. If you have dependent variables, u and v, and you see the expression, uv, you have to apply the product rule, and you will get as the derivative of uv: 
         dv       du
   u     +  v   
     dt       dt
Each of the above is an example of implicit differentiation.

Question 6: What is the problem asking for? Very often it is asking for a rate. That means it is asking for the derivative of one of your dependent variables. In the doggie problem, it asked for the rate at which the radius decreases. We see "rate" and "radius" in the same phrase, and that indicates that the problem is asking for the derivative of radius with respect to the independent variable, which in this case is time. We declared r to be our symbol for the dependent variable, radius, and t to be our symbol for the independent variable, time. So what the problem is asking you to solve for is dr/dt. Look at the equations you have and identify where this term occurs and how you might solve for it in terms of the other variables. Then do so.

Question 7: What variables and derivatives does the problem give actual values for? In the doggie problem it stated the thickness of the paper, the rate the paper was being pulled, and the radius at which you were to establish the rate (observe that the thickness is neither a dependent nor an independent variable -- it is a constant. That is because it does not change as the dog pulls the paper.) We did identify length of paper pulled as a dependent variable. We observe that the problem gives a rate for that, which means that it assigns a value to the derivative of length of paper pulled. It also assigns a value to the radius (and not its derivative). Once you have identified all the values given, go back to the equation where you solved for what the problem was asking for and plug all the values in. That will enable you to get an answer.

Some Worked Examples

Example 1: Two taxicabs begin at the same time at the intersection of Park Ave and 59th St. One taxicab heads uptown (North) on Park Ave at 40 mph. The other heads west on 59th St at 30 mph. Both have the unbelievable good fortune not to be stopped by traffic lights or slowed by traffic. When the taxicab on Park Ave. has gone half a mile, how fast is the distance (as the New York crow flies) between them increasing?

Answering Question 1: The problem asked "how fast." So the independent variable is time, t.

Answering Question 2: The problem talks of distance, and indeed we have distance north of Park and 59th and we have distance west of Park and 59th. We'll call them y and x respectively. The problem asks for the distance between the taxicabs, so that is also a dependent variable, which we shall call, s. Observe that these are all functions of time, since both taxicabs are moving.

Answering Question 3: There are no hidden aspects of taxicabs that are relavent to this problem, so there are no inferred variables.

Answering Question 4: There are two relationships you need to know about in this problem. One is that the taxicabs are traveling at right angles to each other. This means that the Pythagorean distance formula applies. The distance, s between the taxicabs is the hypotenuse of the right triangle formed by the line connecting the northbound taxicab with Park and 59th and the line connecting the westbound taxicab with Park and 59th. The lengths of those sides are y and x respectively. So you have the relationship: 

   s2  =  x2 + y2
There is another relationship in this problem that we can infer from our experience doing motion problems in junior high school. The problem gives us the speeds of the taxicabs and that they start from the same point at the same time. Remember that the northbound taxicab goes 40 mph and the westbound one goes 30 mph. So we can conclude that at any time: 
    y      x
       =                                                          eq. 8.2-6
   40     30
or indeed that 
   3
     y  =  x                                                      eq. 8.2-7
   4

Answering Question 5: This just means taking the derivatives of the relationship equations we got when we answered question 4. For the Pythagorean relationship (eq. 8.2-5), that gives: 

      ds        dx        dy
   2s     =  2x     +  2y                                         eq. 8.2-8
      dt        dt        dt
Taking the derivative of the other relationship yields 
   3 dy     dx
         =                                                        eq. 8.2-9
   4 dt     dt
which is the same as saying that three fourths of the speed of the northbound taxicab is equal to the speed of the same as the speed of the westbound taxicab. And we already knew that.

Answering Question 6: The problem is asking for the rate at which the distance, s, between the two taxicabs is increasing. So it is asking for ds/dt. Observe that this parameter already appears in one of our equations. To solve for it, we simply have to divide the derivative of the Pythagorean equation (eq. 8.2-8) by 2s. 



   ds     1
       =   
   dt     s




 




  dx       dy
x     +  y   
  dt       dt










                                      eq. 8.2-10









Answering Question 7: Now all we have to do is plug in numbers
for all the parameters other than ds/dt into the above and
we will have a value for ds/dt.  So what numbers were given
in the problems?  Only that northbound speed is 40 mph:


   dy
       =  40
   dt



and the westbound speed is 30 mph:


  dx
      =  30
  dt



Also that at the moment we want to know the speed, the northbound taxicab
is half a mile north of Park and 59th:


  y  =  0.5



In order to complete this step we still have to know x and s.
We already determined that x = (3/4)y.  Substituting 0.5
for y we find x = 0.375.  As for s, we
have the Pythagorean distance formula (eq. 8.2-5) to determine s from x
and y:


          _______      _______________
   s  =  Öx2 + y2  =  Ö0.140625 + 0.25  =  0.625                  eq. 8.2-11



When I put all the numbers into the equation that resulted from answering
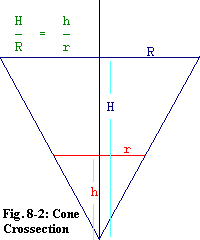
question 6, I get ds/dt = 50 mph




Example 2:
A solution drains through a filter-funnel at a rate of 10 cc/minute.
From the center point of
its mouth to its apex, the funnel is 10 cm.  At its mouth it is
12 cm in diameter.  How fast is the solution-level dropping when there
are 200 cc left in the funnel?  (Assume that the funnel is a right
circular cone)  For reference, the volume of a cone is given by


         1
   V  =    pr2h                                                   eq. 8.2-12
         3



where V is the volume, r is the radius of the base, and
h is the cone's height from base to apex.




Answering Question 1: The problem asks, "how fast," so
clearly the independent variable is time, t.




Answering Question 2: The problem mentions the solution-level,
the volume, and the rate at which volume is being lost.  So
clearly solution-level, h, and volume, V, are dependent
variables.  The rate at which volume is being lost is the derivative of
volume, so it is dV/dt.




Answering Question 3: Think about the situation.  You know that
the funnel is a cone.  But the volume of solution in the funnel is also
a cone, although this cone shrinks as the solution flows out.  The top
surface of the solution is a circle.  And the amount of volume of solution
is related to the radius of that circle by the volume formula for a cone
(given above).  So that radius, r, is also a dependent variable.




Answering Question 4: The volume of a cone formula is a relationship
that the problem gave us.  Again it is:


         1
   V  =    pr2h                                                   eq. 8.2-12
         3













There is another relationship you can get by what you know about cones.
Since the diameter of the base of the funnel is given as 12 cm, clearly
the radius of the base is 6 cm.  The height is given as 10 cm.  So the
ratio of height to radius is 10/6 = 5/3.  But it
is an intrinsic property of cones that the radius of its skirt increases
in linear proportion to the distance along the axis from its apex.  That
means that if the ratio of the big funnel-cone's height to base-radius is
5/3, then the smaller cone that is the volume of solution must
have the same ratio of height to base-radius.
Figure 8-2 shows how the triangular crossection of a cone leads to
this conclusion (recall studying similar triangles in geometry).
The height of the
smaller cone is the solution level, which we have called, h, and
is a dependent variable in this problem.  The
base radius of that smaller cone we have called, r, and it is
also a dependent variable.  From this discussion we now know that:





Cone Crossection







         3
   r  =    h                                                      eq. 8.2-13
         5





Answering Question 5: There are two ways you could go at this point.
One is simply to take the derivative of the volume-of-a-cone formula (eq. 8.2-12), which
is the hard way, but does lead to a solution.  I'll show you the easy way
first, and then demonstrate that the hard way gets you to the same place.
The easy way is to observe that you can make a substitution for r
before you take the derivative of the volume formula:




         1
   V  =    p
         3




 




3
  h
5









2





       3
h  =    
      25




 ph3                                   eq. 8.2-14






Now that we have reduced the number of variables by one we take the derivative
of the above:


   dV      9      dh
       =     p  h2                                                 eq. 8.2-15
   dt     25      dt



But suppose we had just taken the derivative of volume formula without
first making the convenient substitution.  Since the volume formula (eq. 8.2-12)
contains the product of two dependent variables (that is it contains
r2h) we have to use the
product rule.  When you
do you get




   dV     1
       =    p
   dt     3




 




    dr
2rh     +
    dt




  r2




 dh
   
 dt










                                  eq. 8.2-16






If you made the substitution at this point, that is replaced r with
3h/5 into eq. 8.2-16, what would happen?  You'd still be left with
a dr/dt term, but you can substitute that as well by taking the
derivative of:

         3
   r  =    h                                                      eq. 8.2-17a
         5



to find that


   dr     3 dh
       =                                                          eq. 8.2-17b
   dt     5 dt



I'll let you take that substitution the rest of the way.  If you make no mistakes,
you will end up with the exact same equation we got by substituting first and
then taking the derivative.




Answering Question 6: The problem asks for the rate at which the
solution level is dropping.  The solution level is given by the dependent
variable, h.  So the rate of change of the solution level is
dh/dt.  And so that is what we solve for.


   dh    dV 25  1                                                 eq. 8.2-18
       =         
   dt    dt 9p  h2






Answering Question 7: The problem gives
dV/dt = -10 cc/minute (the minus sign
tells you that the volume in the funnel is decreasing).
But the problem doesn't give a value
for h.  So what do we do?  The problem does tell us to find the
rate that the level is decreasing when the volume of solution left in
the funnel is 200 cc.  That is the same as saying, when
V = 200 cc.  And we know from eq. 8.2-14 that

          3
   V  =     ph3                                                   eq. 8.2-19
         25



From that you can solve for h by:





  h  =





  




25
   V
3p









1/3
                                                   eq. 8.2-20






Since V is given, from here it's just a matter of poking
your calculator keys to get an answer.  I get
h = 8.0953 cm, and
dh/dt = -0.13492 cm/minute (note that
the minus sign indicates that the level is going down, as
we would expect if the solution is draining out).




Example 3:
A board that is 96 inches long rests with one end on top of a 12 inch high curb.
The other end rests on the pavement beneath the curb, which is assumed to be
flat.  The lower end is slid along the pavement toward the curb at
a rate of 1 inch per second.  When there
is 36 inches left between the end of the
board and the base of the curb, how fast is the free end of the board moving?
And at what rate is the angle of the board changing?





This problem is a step up in level of difficulty from the two that preceded
it.  But the difference is tantamount to the difference between untying one
knot and untangling an entire snarled wad of yarn.  The techniques are the
same, you just have to do more of them in this problem than in the last two.
But like the snarled wad of yarn, you find an end then methodically work
it back through all the loops and tangles, and if you keep at it long
enough it will be unsnarled.




Answering Question 1:
Again the problem is asking "how fast" and "at what rate,"
so it is clear that the independent variable is time, t.






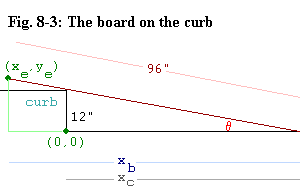
Answering Question 2:
The position of the lower end of the board, or more specifically its
distance from the curb, is clearly a dependent variable.  Let's call
that xc.  The rate at which that end moves is also
the rate at which xc decreases.  And that rate is
dxc/dt.  There is also the position of the other
end of the board.  But it has both a horizontal and vertical position.
So let's call them xe and ye
respectively, and we shall reference them from the base of the curb.
Finally there is the angle of the board, q,
which we shall consider in radians referenced from horizontal.
Figure 8-3 shows all
the dimensions of this problem.  Observe that the way the diagram
is drawn, xe is negative.




Answering Question 3:
When you draw a diagram of this problem, it becomes clear that there
is an important variable that is not mentioned in the problem.
That is the horizontal distance from the lower end of the board
to the spot on the ground immediately below the upper end of the
board.  Call this xb.  Also, if the angle
of the board is a dependent variable, perhaps we might consider
the slope of the board also as a dependent variable, m.




Answering Question 4:
So what are the relationships among the variables here?
Clearly there is a right triangle present here, so the
Pythagorean distance formula
applies.  From the diagram we can see that


   962  =  xb2 + ye2                                              eq. 8.2-21



Now look at the two base lengths, xb and xc.
Notice that the length from (0,0) to (xc,0) added to
the length from (0,0) to (xe,0) is exactly equal to
the length, xb.  But since xe is negative,
the relationship is:


   xc - xe  =  xb                                                 eq. 8.2-22



Look at the diagram again.  Do you see the similar triangles?  The length,
xc, forms the smaller triangle, and the length, xb,
forms the larger one.  By the rule for similar triangles we have:


   ye        ye        12
       =           =       =  -m                                  eq. 8.2-23
   xb     xc - xe      xc



Observe that we put a minus sign in front of the slope, m,
because the way the board is drawn in the diagram, it is sloping
down. And finally, from trigonometry we have


   -m  =  tan(q)                                                   eq. 8.2-24a



or equivalently


   arctan(-m)  =  q                                                eq. 8.2-24b



Again observe that there is a minus sign on the slope, m, because
the board is sloping down the way it is drawn in the diagram.
You also have by trigonometry:


   96 cos(q)  =  xb                                                eq. 8.2-24c

   96 sin(q)  =  ye                                                eq. 8.2-24c







Answering Question 5:
All we need to do for this one is take the derivatives of each of the relationships
listed in the question 4 paragraph above.  So taking the derivative of both
sides of eq. 8.2-21:


             dxb         dye
   0  =  2xb      +  2ye                                          eq. 8.2-25a
             dt          dt



from which you can divide out a factor of 2 to get:


            dxb        dye
   0  =  xb      +  ye                                            eq. 8.2-25b
            dt         dt



Taking the derivative of eq. 8.2-22 is pretty easy:


   dxc     dxe     dxb
        -       =                                                 eq. 8.2-26
   dt      dt      dt



On eq. 8.2-23, it turns out the we will mostly be interested in taking
the derivative of
12/xc = -m:


     12  dxc       dm
   -          =  -                                                eq. 8.2-27a
     xc2  dt        dt



and the minus signs cancel to give:


   12  dxc     dm
            =                                                     eq. 8.2-27b
   xc2  dt      dt



From the trig equations, the arctan equation (8.2-24b) turns out to be
more useful than the tan equation (8.2-24a).  Its derivative
(remembering that the derivative of arctan(x) is
1/(1 + x2))
is


     -1   dm     dq
              =                                                   eq. 8.2-28b
   1 + m2 dt     dt



We also have from 8.2-24c and 8.2-24d respectively:


             dq      dxb
  -96 sin(q)      =                                                eq. 8.2-28c
             dt     dt


             dq      dye
   96 cos(q)      =                                                eq. 8.2-28d
             dt     dt







Answering Question 6:
Although this problem is harder than the other two, it is not the calculus part
that makes it harder.  We have already done all the calculus we need to do
on this problem.  All that is left to be done is the algrebra and trig.
There is more of it to do on this problem than on the others, but
it is still stuff you have had before.  The problem asked for the speed
of the free end, which will be a combination of dxe/dt
and dye/dt.  And it also asked for the rate at which
the angle, q, is changing, which would
be dq/dt.  At this point we have
all the equations we need to solve all this.  All we need to do is organize
them in a way that makes sense and substitute one into another until we
get a solution.




It turns
out that dq/dt is easier to solve for
than the either of the other two variables.
So let's do that one first.  Remember that the distance from the low end
of the board to the base of the curb, xc, is given.
So is the rate at which it is being pushed, dxc/dt.
From those two we can get the slope of the board, m, from eq. 8.2-23
and we can get the rate at which that slope is changing,
dm/dt, from eq. 8.2-27b:


   ye        ye        12
       =           =       =  -m                                  eq. 8.2-23
   xb     xc - xe      xc


   12  dxc     dm
            =                                                     eq. 8.2-27b
   xc2  dt      dt



Once we know m and dm/dt, eq. 8.2-28b will give us
dq/dt:


     -1   dm     dq
              =                                                   eq. 8.2-28b
   1 + m2 dt     dt



We have expressions for dxb/dt and dye/dt
in equations 8.2-28c and 8.2-28d. But they involve the sine and cosine of
q, which we do not yet know.  But we do know what
tan(q) is from eq. 8.2-24a. And, remembering
that tan(x) = sin(x)/cos(x) and
sin2(x) + cos2(x) = 1, you can easily derive:


                   1
   cos(x)  =                                                      eq. 8.2-29a
              Ö1 + tan2(x)


                 tan(x)
   sin(x)  =                                                      eq. 8.2-29b
              Ö1 + tan2(x)



And don't just take my word for it.  Derive these for yourself.  Eq. 8.2-24a
tells us that -m = tan(q) .
So from the trig identities in equations 8.2-29a and 8.2-29b we have:


                 1
   cos(q)   =                                                      eq. 8.2-30a
              Ö1 + m2


                -m
   sin(q)   =                                                      eq. 8.2-30b
              Ö1 + m2



Substituting those into equations 8.2-28c and 8.2-28d and substituting
dq/dt from eq. 8.2-28b, you have:


          -m       dm     dxb
   96                  =                                          eq. 8.2-30c
      (1 + m2)3/2   dt     dt


          -1       dm     dye
   96                  =                                          eq. 8.2-30d
      (1 + m2)3/2   dt     dt



Finally we observe that we can get dxe/dt using
eq. 8.2-26.  Solving that for dxe/dt gives:


   dxc     dxb     dxe
        -       =                                                 eq. 8.2-31
   dt      dt      dt








Answering Question 7:
The problem tells you that xc = 36 inches.  It also
tells you that
dxc/dt = -1 inch/sec (it's negative because the
low end of the board is moving to the left so xc is
decreasing).  Now we take it step by step.  First,
eq. 8.2-23
tells us that m = -1/3.  From
eq. 8.2-27b you get
dm/dt = -1/108.  From
eq. 8.2-28b you get
dq/dt = 1/120 radian/sec.
From eq. 8.2-30c you get
dxb/dt = -0.2529822 inches/sec (that is,
xb is decreasing), and from
eq. 8.2-30d you get
dye/dt = 0.7589466 inches/sec (that is the
free end of the board is getting higher).  From
eq. 8.2-31 you have
dxe/dt = -0.7470178 inches/sec (that is the
high end of the board is moving to the left).





Finally, now that we have values for dxe/dt and
dye/dt, which are the x and y
components of the speed of the free end of the board, how do we find
the composite speed of that end?  Velocities that are at right angles
to each other combine according to the Pythagorean rule (you can prove that
by drawing a diagram that shows the movement of the end of the board
in the x and y directions during a short interval of
time, Dt, and then taking the limit
as Dt goes to zero). So if we allow
v to be the composite speed, then






   v2  =





  




dxe
   
 dt









2
  +





  




dye
   
 dt









2
                                      eq. 8.2-32






Solving for velocity, my calculator tells me that
v = 1.0649110 inches/sec.




Exercises



1)
Return to the taxicab problem, but this time give the westbound
taxicab a quarter mile head start. Keep everything else the same.  When the
northbound taxicab has gone half a mile from its starting
position, how fast is the distance between the two taxicabs increasing?
You should be able to get through this one using the worked example
on this page as a model.  When you are done,
click here to view the solution.




2)
We shall remain in New York City for this problem, which is similar to the
taxicab problem.  The Verazzano-Narrows bridge, which
connects Brooklyn with Staten Island, has a span length of about 4200 feet.
Assume that the entire roadbed is 200 feet above the water.  A small motor
boat traveling perpendicular to the bridge is 1000 feet away from passing
under the midspan of the bridge.  The boat is cruising 20 feet per second
toward the bridge.
At the same time a Brooklyn-bound runner on the bridge is passing the tower on
the Staten Island side (the towers are at either end of the span, so the runner
is entering the span).  The runner moves at 10 feet per second along the bridge.
How fast is the distance between the boat and the runner decreasing?





Although this one has the additional wrinkle of being in three dimensions
instead of two (like the taxicabs), the methods are the same.  Remember
that the Pythagorean distance formula
works just as well in three dimensions as it does in two.  So go as far
as you can with this before clicking here
to see the solution.




3)
Here's one that is very important in mechanics.  A circular track has radius,
r.  A train moves around the track at
w radians/second.  That means
that if the center of the circle is at (0,0), the position of the
train as a function of time, t, is:


   ( r cos(wt), r sin(wt) )



Find the x and y components of the train's velocity (which is
the first time derivative of position) and the x and y components
of its acceleration (which is the second time derivative of position).
What can you observe about the direction of the train's velocity and acceleration
in relation to its position on the track?  And how would the magnitude of
velocity and acceleration be effected if you varied r? or if you varied
w? Click here
to view solution.




4)
A rocket is launched vertically and travels at 100 meters per second. A tracking
radar is 500 meters from the launch site.  When the rocket is 800 meters high,
how fast must the radar antenna slew (in radians per second) in order to track
the rocket?
Click here to view solution.




5)
Two sticks, one 8 feet long, the other 12 feet long, are joined end-to-end with
a hinge.  The free end of the 8 foot stick is fixed to the ground.  The free
end of the 12 foot stick is slid along the ground toward the free end of the
8 foot stick at one foot per second.  The whole assembly is held so that the
triangle formed by the two sticks and the ground is always perpendicular to
the ground.  At what rate is the angle between the 8 foot stick and the
ground increasing when the distance between the free ends of the two sticks
is 5 feet? Hint: Use the
law of cosines.
When you've worked this one out, click here to view solution.




6)
The celebrated actor, Tyrone Olivier, is exactly 6 feet tall.
Tonight he delivers a stirring soliloquy on stage. For dramatic effect
he is illuminated only by a single footlight, which is at the same level
as the floor of the stage.  24 feet behind the footlight is the
vertical backdrop of the stage.  As Tyrone Olivier nears the climax of
his soliloquy, he begins walking toward the audience (and toward the
footlight) at 2 feet per second. When he is 8 feet
from the footlight, at what rate is his shadow on the backdrop increasing
in height? Hint: Make a diagram and use similar triangles.
Click here for solution.









Dimensional Checking (sometimes called Units Checking)



Does Your Answer Pass the Smell Test?




In the early paragraphs of this section I suggested that you always do
reasonableness checks on your answers to problems like these. The tests
I suggested were things like making sure that the sign of the answer
made sense and that the answer seemed in the right ballpark. But till
now I have completely skipped the most powerful method of checking
your answer, and that is checking it dimensionally.





If you have taken or are taking chemistry or physics, you are likely
to have already encountered this method. Besides working on chemistry
and physics problems, it works on related rate problems as well (and
just about all other word problems too). If you are going into engineering,
this method will serve you well for many years to come.





Back in grade school when you learned to do word problems,
your teacher, if he or she was any good, told you, "Always
write in the units." This was and still is excellent advice.
In the real world most quantities have
units like meters, dollars, pints, degrees C, and so on.
If you drive 60 miles per hour, you are also driving
88 feet per second. So if you had to write down how fast
you were going, which is correct, 60 or 88? Neither!
You could be indicating leagues per sidereal day for
all I know.
But both "60 miles per hour" and "88 feet per second" are correct
answers.  And the two quantities are indeed equal, despite
the difference in the numerals. This is because the
"miles per hour" and the "feet per second" are as much a part
of each quantity as the 60 or the 88.





The real beauty of having units attached to your quantities
is that you can do an arithmetic of sorts on the units themselves.
And when you are done, if the problem asks, "how fast
is Jane running?" the answer better come out having units
of velocity. If it doesn't then you did something wrong
somewhere and your answer is probably wrong.





Let's take a very simple example. Light travels
299,799 kilometers in a second. What is the speed
of light in kilometers per year
if there are 31,557,600 seconds in a year?


           km               sec                       km
   299,799     × 31,557,600       =  9.460937 × 1012     
           sec              year                     year



Remember that whenever you see the word, "per," it means the same as
"divided by" or "over." And as it is with numbers, so it is with
units. "Kilometers per second" means the same thing as
"kilometers over seconds." That is how we wrote it here. Same thing
with "seconds in a year." It also means "seconds per year,"
which means "seconds over years." The problem asks for an answer
in "kilometers per year." You can see that when we multiply
"kilometers over seconds" times "seconds over years,"
the seconds cancel and we are left with "kilometers over seconds,"
which are the units the problem calls for. Since the units came out
right, there is a good likelihood that we did the problem correctly.





Now suppose a problem asked, how many seconds does it take light
to travel 1.5 × 108 kilometers?
Here is the setup for that:


                       1    sec
   1.5 × 108 km  ×               =  500 sec
                    299,799  km



The problem asks for an answer in seconds.
Observe how, in order to get kilometers to cancel and for seconds to come out
on top, we had to take the reciprocal of "kilometers per second" and multiply
by it. When you take
the reciprocal of the units, you also take the reciprocal of the number
attached to them. Or equivalently you could have just divided by the
kilometers per second quantity. So the units are cluing you in on what gets
multiplied and what gets divided to get the correct answer.





Some quantities have no units. These are called dimensionless
quantities. For example, p is the
ratio of the circumference of a circle to its diameter. It doesn't
matter how large the circle is or in what units you measure the
circumference and diameter (as long as you use the same units
for both), the value of p
is still the same. If c is the circumference in furlongs
and d is the diameter in furlongs, then


   c furlongs
               =  p
   d furlongs



The units cancel in this case, no matter what units you use.





Angles, and particularly angles measured in radians are
dimensionless. Remember that the definition of radian measure
was that you take the distance around the circle the angle takes you,
and then you divide that distance by the radius of the circle. That
is the quotient of two lengths, so the length-units cancel leaving only
the dimensionless ratio.





Units can be raised to a power. You know very well
that if you multiply the height of a rectangle by its width, you
get its area. If both the height and width are in inches, then
the area comes out in square inches, which is the same
as inches squared.


   14 in × 7 in  =  98 in2



Not only length-units can be raised to a power. It can happen
to other types of units as well. For example,
acceleration measures how many meters per second an object's
velocity gains per second. So the units of acceleration
would be meters per second per second.


     meters
           
       sec         meters
                =        
       sec          sec2



You can see how that's the same as meters per second squared.





You can only add quantities that have the same
units. In other words, you can't add apples to oranges. So if you find
yourself adding two quantities whose units differ, you made a mistake somewhere.
The units that the sum has are the same as the units of each of its summands.





When you use trig functions, inverse trig functions, logs or exponentials,
the argument must be dimensionless. You can't take the sine of 3 centimeters
or the exponential of 40 grams. The thing you take the sine or exponential (or
any of the other trig or log functions) of must not have any units. And the
value the function returns is also dimensionless. For example, if you have
an exponential function of time, the time, t, will always be multiplied
by a rate, k, whose dimensions are inverse time. Suppose t is
in seconds. Then there would be a rate, k, whose dimensions are
in per second (that is inverse seconds). Suppose
 k = 0.001 /second. Then you could form the
exponential function


   f(t)  =  e-kt  =  e-0.001t



Of course this equation gives you a value, f(t), that is
dimensionless. If the result had to have dimensions of, say watts,
then the exponential would have to have a multiplier that had
dimensions of watts. For example, you might have
 P = 3 × 107 watts. Then
you could have


   g(t)  =  P e-kt  =  3 × 107 watts × e-0.001t



The only possible exception to this rule is the log. Since a quantity
is the product of its units and a number, you can argue that





  ln










1400 cm
       
 14 cm










  =  ln(1400 cm) - ln(14 cm)  =  ln(1400) - ln(14) + ln(cm) - ln(cm)






but only if you are willing to accept the existence of the abstraction,
ln(cm), and only if, in the end, such abstractions all cancel out.
The log still returns a dimensionless result regardless.





Units conversion factors, deep down, are all equal to one.
Consider that


   1 hour  =  60 minutes



That means that if you divide out 1 hour, you get the units
conversion factor of


            minutes
   1  =  60        
              hour



When you convert 14 hours to minutes, you do:


                 minutes
   14 hours × 60          =  840 minutes
                   hour



Isn't it true that 14 hours and 840 minutes are
precisely the same length of time? The two quantities are equal.
Which means that 60 minutes/hour must be
equal to 1 and nothing else.





A derivative always takes the ratio of units.
For example, when you take the derivative of distance (say in meters)
with respect to time (say in seconds), the derivative would have
units of meters per second. If you have any dependent variable,
v, and you take its derivative with respect to an independent
variable, t, to get dv/dt, the result will have units that are v's
units divided by t's units.





Units of second derivatives are tricky. If you take the second derivative
of a dependent variable, v, with respect to the independent variable, t,
to get


   d2v
      
   dt2



this second derivative will have units that are the units of v divided
by the square of the units of t.  Note that you only
square the denominator units and not the numerator units. This makes
sense because the second derivative is the derivative of the first derivative.
So you take the units of the first derivative and divide it by the units
of the independent variable.
For example,
acceleration is the second time derivative of distance. If you are using
meters and seconds, acceleration has units of


   meters
         
    sec2



This same principle goes with higher derivatives too. If you take the nth
derivative of v with respect to t, the units you end up with
are the units of v divided by the units of t taken to the nth
power. Only the denominator units are taken to the nth power,
not the units of v.





Let's dimensionally check a solution to one of the problems in this section.
We'll do problem 4. Here you were given
the rocket's altitude, h in meters, the distance to the radar,
x in meters, and the rocket's speed, dh/dt in meters
per second. The problem asks for a rate,
dq/dt, in radians per second. Since
radians is dimensionless, that is the same as plain old "per second"
(when the "per" is not preceded by any units, it is assumed
that the numerator of the units is dimensionless, which is to say
that the numerator is just 1). The solution equation for the problem
is


   dh    x        dq
               =    
   dt x2 + h2     dt



On the left we have dh/dt, which is in meters per second.
The next factor has x in the numerator, so the numerator
is meters. The denominator has the sum of x2
and h2. Both x and h have
units of meters, so their squares both have units of square meters.
Because those units are the same, it is ok to add those two quantities.
To the right of the equal sign is dq/dt,
which we already determined has units of per second. So, expressing this
equation only in its units we have


   meters  meters      1
                   =     
     sec   meter2     sec



I'm sure you can convince yourself that meters and meters squared all cancel
out of the left-hand side of this, leaving only per second on both the left
and right of the equal. So the units agree. The original equation smells good.




 
Return to Table of
Contents
 
Move on to 
Name That Function


email me at hahn@netsrq.com