Definition. Let \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \) be vectors in \( \mathbb R^n \). The span of \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \), written \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \), is the set of all linear combinations of \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \).
Example 1. Let \( \bbm u = \vecthree 5 {-3} 0 \) and \( \bbm v = \vecthree {-2} 1 3 \). Give three examples of elements of \( \mbox{Span} \{ \bbm u, \bbm v \} \).
Every vector in \( \mbox{Span} \{ \bbm u, \bbm v \} \) has the form \( c \bbm u + d \bbm v \) for scalars \( c \) and \( d \). So, we just choose scalars to construct linear combinations: \[ 2\bbm u + 3\bbm v = 2 \vecthree 5 {-3} 0 + 3 \vecthree {-2} 1 3 = \vecthree 4 {-3} 9 \] \[ 0\bbm u + (-2)\bbm v = 0 \vecthree 5 {-3} 0 + (-2) \vecthree {-2} 1 3 = \vecthree 4 {-2} {-6} \] \[ \frac 1 2 \bbm u + \frac 2 3 \bbm v = \frac 1 2 \vecthree 5 {-3} 0 + \frac 2 3 \vecthree {-2} 1 3 = \vecthree {7/6} {-5/6} 2. \Box \]
Example 2. Let \( \bbm v_1 = \vectwo 1 {-3}, \bbm v_2 = \vectwo 0 5, \bbm v_3 = \vectwo {-2} 1 \), and \( \bbm b = \vectwo 3 4 \). Is \( \bbm b \) in \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \bbm v_3 \} \)?
In order for \( \bbm b \) to be in \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \bbm v_3 \} \), we would have to be able to write \( \bbm b = c_1 \bbm v_1 + c_2 \bbm v_2 + c_3 \bbm v_3 \) for some scalars \( c_1, c_2\), and \( c_3 \). To find out whether this is possible, we solve the vector equation \( x_1 \bbm v_1 + x_2 \bbm v_2 + x_3 \bbm v_3 = \bbm b \) in the normal way.
The augmented matrix corresponding to this vector equation row reduces like this: \[ \begin{bmatrix} 1 & 0 & -2 & 3 \\ -3 & 5 & 1 & 4 \end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 & -2 & 3 \\ 0 & 1 & -1 & 13/5 \end{bmatrix} \]
Since there is no pivot in the last column, the vector equation is consistent. This tells us that, yes, \( \bbm b \) is in \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \bbm v_3 \} \). \( \Box \)
There are many different equivalent ways to think about what \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \) represents:
Given vectors \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \) and \( \bbm b\), you may be asked the question "Is \( \bbm b \) in \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \)?" (see Example 2). To answer this question, follow this outline:
When \( p \) is a small number, we can visualize \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \). Remember that \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p\) is a finite list of vectors, but \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \) is a (usually) infinite set of vectors!
If \( p = 1 \), then \( \mbox{Span} \{ \bbm v_1 \} \) is the set of all scalar multiples of \( \bbm v_1 \). If \( \bbm v_1 = \bbm 0 \), then all of these multiples are the zero vector, so \(\mbox{Span} \{ \bbm v_1 \} \) is \( \{ \bbm 0 \} \), the set containing only the zero vector. If \( \bbm v_1 \) is any nonzero vector, then we can visualize \(\mbox{Span} \{ \bbm v_1 \} \) as a line through the origin.
Example 3. Let \( \bbm v = \vectwo 1 2 \). Draw several elements of \(\mbox{Span} \{ \bbm v \} \).
We plot the vectors \( c\ \bbm v = c \vectwo 1 2 = \vectwo c {2c} \), which all lie on the line \( y = 2x\):
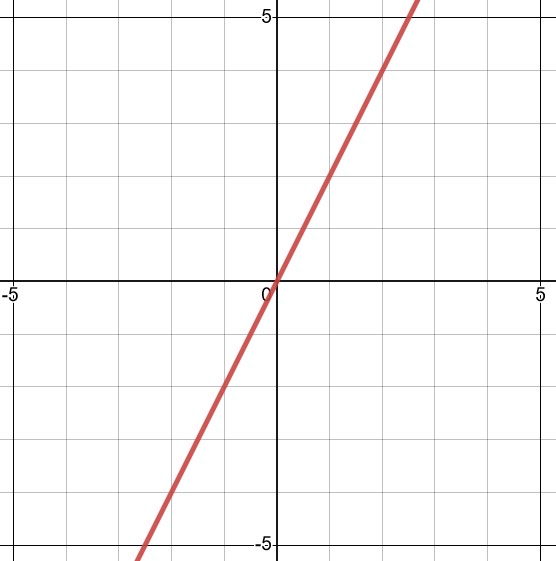
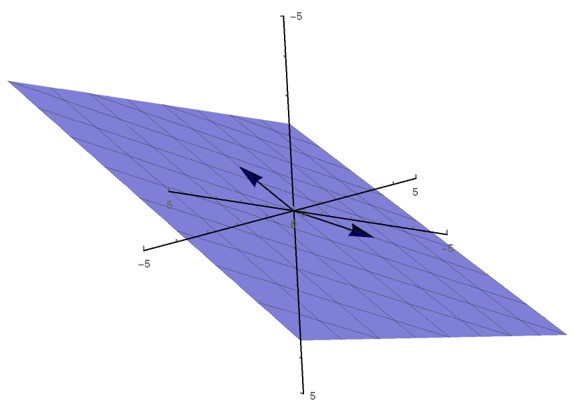
When \( p = 2\), the span of \( \bbm v_1 \) and \( \bbm v_2 \) contains all vectors of the form \( c_1 \bbm v_1 + c_2 \bbm v_2 \) for scalars \( c_1 \) and \( c_2 \). If either \( \bbm v_1 \) or \( \bbm v_2 \) is the zero vector, or if one of these vectors is a scalar multiple of the other, then \(\mbox{Span} \{ \bbm v_1, \bbm v_2 \} \) is the same as the span of just one vector. Otherwise, in the general case, \(\mbox{Span} \{ \bbm v_1, \bbm v_2 \} \) can be visualized as a plane:
Earlier, we discussed how to answer the question "Is \( \bbm b \) in \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \)?" Sometimes, depending on the vectors \( v_1, \bbm v_2, \ldots, \bbm v_p\), the answer to this question is always "yes," no matter what \( \bbm b \) is.
Example 4. Let \( \bbm v_1 = \vectwo 1 {-3} \) and \( \bbm v_2 = \vectwo 0 5 \). Show that every vector \( \bbm b = \vectwo {b_1} {b_2} \) in \( \mathbb R^2 \) is in \( \mbox{Span} \{ \bbm v_1, \bbm v_2 \} \).
Following the outline we discussed earlier, we set up the vector equation \( x_1 \bbm v_1 + x_2 \bbm v_2 = \bbm b \) and try to show that this equation is consistent, no matter what \( \bbm b \) is. We set up the augmented matrix: \[ \begin{bmatrix} 1 & 0 & b_1 \\ -3 & 5 & b_2 \end{bmatrix} \]
Even though we don't know what the values of \( b_1 \) and \( b_2 \) are, we can proceed with our normal row-reduction process. The only thing we will have to be careful about is to never divide by \( b_1 \) or \( b_2 \), since we don't know whether these values might be zero. Our first row-reduction step is to replace Row 2 by the sum of itself and 3 times Row 1: \[ \begin{bmatrix} 1 & 0 & b_1 \\ -3 & 5 & b_2 \end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 & b_1 \\ 0 & 5 & 3 b_1 + b_2 \end{bmatrix} \]
At this point we can stop because the matrix is in echelon form. This is enough for us to be able to tell that there is no pivot in the last column. We can tell that this is true, even though we still don't know what \( b_1 \) and \( b_2 \) are! This shows that the equation \( x_1 \bbm v_1 + x_2 \bbm v_2 = \bbm b \) is consistent no matter what \( \bbm b \) is, and so every vector in \( \mathbb R^2 \) is in \( \mbox{Span} \{ \bbm v_1, \bbm v_2 \} \). \( \Box \)
The situation in Example 4 leads us to a new definition involving the word "span":
Definition. Let \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \) be vectors in \( \mathbb R^n \). The vectors \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \) are said to span \( \mathbb R^n \) if every vector in \( \mathbb R^n \) is in \( \mbox{Span} \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \).
In the situation of Example 4, we say "\( \bbm v_1 \) and \( \bbm v_2 \) span \( \mathbb R^2 \)" or "\( \{ \bbm v_1, \bbm v_2 \} \) spans \( \mathbb R^2 \)." Notice that, in this sense, we are using the word "span" as a verb rather than a noun. Here's how we distinguish the two ways that we use the word "span":
| "Span" as a noun | "Span" as a verb |
|---|---|
| The span of \( \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \) is the set containing every vector that can be written as a linear combination \( c_1 \bbm v_1 + c_2 \bbm v_2 + \cdots + c_p \bbm v_p \). | The set \( \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \) spans \( \mathbb R^n \) if every vector in \( \mathbb R^n \) can be written as a linear combination of \( \bbm v_1, \bbm v_2, \ldots, \bbm v_p \). |
This new sense of the word "span" as a verb raises a new question: How can we tell when a set of vectors \( \{ \bbm v_1, \bbm v_2, \ldots, \bbm v_p \} \) spans \( \mathbb R^n \)? We answered a question of this type in Example 4, but we don't (yet) have a good way of answering this question in general. We will learn a general method for answering this question in Lecture 9.
« Lecture 7 Back to Top Lecture 9 »