Lecture 43 - Applications to Image Compression

Using the SVD to Approximate a Matrix

Recall that we can find the singular value decomposition for any matrix \( A = U\Sigma V^T \), where the diagonal entries of \( \Sigma \) are the singular values of \( A \) listed in decreasing order \( \sigma_1 \gt \sigma_2 \gt \sigma_3 \gt\cdots \). Approximate \( A \) by using only the largest (and therefore most significant) singular values.

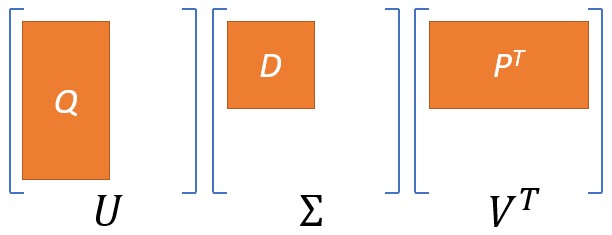
Let \( A \) be an \( m \times n\) matrix with singular value decomposition \( A = U\Sigma V^T \). If \( A \) has \( r \) nonzero singular values, choose \( k \ll r \).

• Let \( Q \) be the \( m\times k \) matrix consisting of the first \( k \) columns of \( U \)
• Let \( D \) be the \( k\times k\) consisting of the first \( k\) rows and first \( k\) columns of \( \Sigma \)
• Let \( P \) be the \( k\times n\) matrix consisting of the first \( k\) rows of \( V^T \)

Note that \( QDP^T \) is the same size as \( A \) and we will see that \( A \approx QDP^T \).

Compressing an Image

We will apply this approximation to compress an image. For now, we will focus on grayscale images. For example, consider this image of a flower:

We can think of every pixel of this image as a number between 0 and 1, with 0 representing a pixel that is completely black and 1 representing a pixel that is completely white. Thus, the image can be represented as a matrix. In this case, the image is 1600 pixels by 1063 pixels, which means that we need approximately 1.7 million numbers to store the image "faithfully." Compressing the image allows us to store it using less space, in exchange for sacrificing quality.

If \( M \) is the matrix representing this image, we can construct the singular value decomposition \( M = U\Sigma V^T \). Choosing \( k = 50 \), we get \( M \approx QDP^T \), where

• \( Q \) is \( 1600\times 50 \) (the first \( 50 \) columns of \( U \))
• \( D \) is \( 50\times 50\) (the first \( 50\) rows and first \( 50\) columns of \( \Sigma \))
• \( P \) is \( 50\times 1063\) (the first \( 50\) rows of \( V^T \))

This approximation reduces the total storage needed to \( 135,\!650 \) total matrix entries, which is a 92% reduction. Computing \( QDP^T \) and gives us an image the same size as the original, but with lower quality:

Color Images

Color images can be represented by three "channels," typically red, blue, and green. Each pixel is therefore represented by three numbers, each representing the amount of red, blue, and green light needed to create the desired color and brightness.

We can then compress the three channel images separately, and then combine them to create the compressed image. Taking \( k=50 \) as before yields the following image (again, with 92% less storage needed):