Section 11: Methods of Integration
© 2000 by
Karl Hahn
This section is still under construction
11.2 Integration Using Your Rear View Mirror
As you drive down a highway, you can sometimes get a good idea of what
the scenery looks like to drivers heading in the opposite direction by looking
in your rear view mirror. That is especially true if the scenery is simple.
The same is true of finding indefinite integrals. If the function is simple, you
can sometimes figure out an antiderivative using only what you know about
derivatives. Indeed we had a table of derivatives
of simple functions. Clearly if the function you want to find the indefinite integral
of appears in the "derivative" (right-hand) column of this table, then an antiderivative
of that function appears in the left-hand column.
Let's start with something very easy. Suppose you want to find the indefinite integral,
|

|
ex dx
|
You already know that if f(x) = ex, then
f'(x) = ex. That is the special property of
the ex function -- that it is its own derivative. So
clearly it must be its own antiderivative as well. The only other thing we have to
do here is stick in the undetermined constant, and we will have the indefinite integral
of ex.
|

|
ex dx = ex + C eq. 11.2-1
|
Now suppose that you had the same problem except with the additional complication that the ex
is multiplied by the constant, A. From your knowledge of derivatives you recall that
if f(x) = Aex, then
f'(x) = Aex. Clearly the function, Aex,
has that same property when A is constant -- that it is its own derivative. So again it must be
its own antiderivative as well. From that you have
|

|
Aex dx = Aex + C eq. 11.2-2
|
Indeed if you took any function, f(x), for which you already knew an
antiderivative, F(x), and you multiplied f(x) by
a constant, A, wouldn't it be true that AF(x) was always
an antiderivative of Af(x)? Think about it. Remember that
F'(x) = f(x). Recall the rule about taking the derivative of
something that is multiplied by a constant (check the page of rules
if you have to). The rules force you to conclude taking the derivative of AF(x) will
give you AF'(x) = Af(x). Since AF(x) is always
an antiderivative of Af(x), it follows that if you know the indefinite integral
of a function, then you can easily find the indefinite integral of a constant times that
same function. In symbols it looks like this (where F(x) is an antiderivative
of f(x))
|

|
Af(x) dx = AF(x) + C = A
|

|
f(x) dx eq. 11.2-3
|
|
Look at equation 11.2-3 carefully. Ignore the middle expression and just regard it as setting the
left-hand expression equal to the right-hand expression. That means that whenever you see a constant
mulitplied times the entire integrand, you can move that constant multiplier outside the integral sign.
(If you remember that an integral is a limit of a Riemann sum, the previous statement is simply the
equivalent of the distributive law over that sum)
Let's see how we can use equation 11.2-3 to work backwards on our old friend, x raised to a power.
Always remember that finding an indefinite integral means
finding an antiderivative. We know from our study of derivatives that the derivative of
f(x) = xp is
f'(x) = pxp-1. This works even when p
is negative and when it is not an integer. So from this we know that an antiderivative
of pxp-1 is xp.
Now suppose that you would like to find the indefinite
integral
|

|
xs dx eq. 11.2-4a
|
where s is a constant.
How do we run the process of taking the derivative of
xs backward? We have to munge the
integrand into pxp-1. We know the antiderivative of
that expression.
For our integrand in equation 11.2-4a to look like pxp-1
we would have make
p-1 = s and equivalently
p = s+1 in order to make the exponent come out right.
If you make this substitution, the indefinite integral that we're after becomes
|

|
xp-1 dx eq. 11.2-4b
|
It still isn't quite right because it isn't multiplied by p. But if p is not
zero, then it's always true that p/p = 1. So the expression in
equation 11.2-4b is the same as:
|
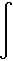
|
p
xp-1 dx eq. 11.2-4c
p
|
Now recall the rule we just learned in equation 11.2-3. Since 1/p
is a constant multplier over the entire integrand, we can factor it to outside the integral sign.
|
1
p
|

|
pxp-1 dx eq. 11.2-4d
|
Now the integrand is indeed the derivative of something that we know. It is the derivative of
xp. So the indefinite integral is
|

|
1
xp-1 dx =
p
|

|
1
pxp-1 dx = xp + C eq. 11.2-4e
p
|
|
Now simply drop the middle expression and substitute back by replacing p with s+1 and p-1 with s
|
Did you catch me playing fast and loose with the algebra here?
In equation 11.2-4e, the right hand side ought to be
1
(xp + C)
p
But does it make any difference? Remember that C is an undetermined constant.
If that is the case, then isn't C/p also an undetermined constant?
Does it matter what we call it? Remember that any constant will do. So the way we have
it in equation 11.2-4e is correct even though I did not strictly adhere to the rules
of algebra. And typically that is the way you will do these problems. You won't add
the undetermined constant in until you have done all the other steps first. Then stick
it in as the last step and you'll be good to go.
|
|
|

|
1
xs dx = xs+1 + C eq. 11.2-4f
s+1
|
|
Equation 11.2-4f works even when s = 0. Note
that when you put in zero for s you have x0 = 1
as your integrand. Hence
|

|
x0 dx =
|

|
1 dx =
|

|
1
dx = x1 + C = x + C eq. 11.2-5
1
|
|
Indeed equation 11.2-4f works with all values of s except
s = -1. Can you see why it fails then?
You'd have a division by zero. But when s = -1,
the integrand is really 1/x. So in that case the indefinite
integral you are trying to find is
|
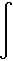
|
1
dx =
x
|
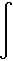
|
dx
eq. 11.2-6a
x
|
Note the second way of writing this indefinite integral. Most textbooks will use this
nomenclature when the integrand is a quotient. That is they will put the dx
in the numerator of the quotient. But the two ways of writing it shown in equation 11.2-6a
mean exactly the same thing.
So where have we seen 1/x as the derivative of something? Check the
table. Doesn't the derivative of F(x) = ln(x)
fill the bill? Since ln(x) is an antiderivative of 1/x, you have
|
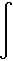
|
1
dx =
x
|
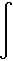
|
dx
= ln(x) + C eq. 11.2-6b
x
|
This indeed is the property of the natural log that causes it to come up so
frequently in physics, chemistry, and engineering. Any model of any phenomenon
that causes you to take the integral of a 1/x style function
will result in a natural log being part of the model.
But what if x is negative? You can't take the log of a
negative number. Does that mean that there is
no indefinite integral of 1/x for that domain?
You only have to make a minor mod to equation 11.2-6b to make it work for
negative x as well.
|
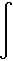
|
1
dx =
x
|
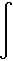
|
dx
= ln|x| + C eq. 11.2-6c
x
|
|
That is the natural log of the absolute value of x.
Look at what happens when you take the derivative (using the
chain rule) of
F(x) = ln|x|. Remember that the
derivative of |x| is sgn(x)
(where sgn(x) = 1 for
x > 0 and
sgn(x) = -1 for
x < 0). Hence
dln|x| 1 1
F'(x) = = sgn(x) = eq. 11.2-7
dx |x| x
So ln|x| is also an antiderivative of 1/x, but
this antiderivative will admit negative values of x.
We already saw what the indefinite integrals of ex and
Aex were. What about
|

|
ebx dx eq. 11.2-8a
|
where b is a constant? Recall that the derivative of
f(x) = ebx is
f'(x) = bebx.
Now lets play the same game we played before. Whenever b
is not zero, you have
|

|
ebx dx =
|

|
b 1
ebx dx =
b b
|

|
bebx dx eq. 11.2-8b
|
And when b is zero, you don't care because e0x = 1, which you
already know how to integrate. In equation 11.2-8b, the right-hand integrand is the derivative of something
we already know -- that is it is the derivative of ebx. Hence
|

|
1
ebx dx = ebx + C eq. 11.2-8c
b
|
This pattern works with any function. If you know that F(x) is an
antiderivative of f(x), then it is always the case (when b
is a nonzero constant) that
|

|
1
f(bx) dx = F(bx) + C eq. 11.2-9
b
|
|
You can see why by taking the derivative of the indefinite integral expression shown above
using the chain rule.
Suppose you wanted to find the indefinite integral of cos(x).
Another glimpse of the table ought to convince
you that sin(x) is an antiderivative of cos(x).
So clearly
|

|
cos(x) dx = sin(x) + C eq. 11.2-10a
|
But what if you wanted to find the indefinite integral of
cos(x+f), where
f is a constant. Notice that when you have
any function, f(x+f), and
you take the derivative
(using the chain rule), you end up with f'(x+f).
It doesn't take a whole lot of vision to see that this same arrangement will work in reverse.
So we see that
|

|
cos(x+f) dx = sin(x+f) + C eq. 11.2-10b
|
or in general, whenever F(x) is an antiderivative of f(x).
|

|
f(x+f) dx = F(x+f) + C eq. 11.2-11a
|
|
for any constant, f. Or even more generally (combining the
three rules for constants we learned on this page),
whenever A, b and f are
constants and F(x) is an antiderivative of f(x), then
|

|
A
Af(bx + f) dx = F(bx + f) + C eq. 11.2-11b
b
|
|
provided that b is not zero.
Suppose you needed to know the indefinite integral of 3 + e-x.
From equations 11.2-3 and 11.2-5 you should be able to see
easily that
|

|
3 dx = 3x + C eq. 11.2-12a
|
And from equation 11.2-9 you should be able to see that
|

|
e-x dx = -e-x + C eq. 11.2-12b
|
So what happens if you take the derivative of the sum of these two results?
Try it. Doesn't that get you back to the original function of
3 + e-x? And doesn't that
mean that
|

|
(3 + e-x) dx = 3x - e-x + C eq. 11.2-12c
|
(Notice again the treatment of the undetermined constant, C. By rights, you should
have 2C in the above, but if C is an undetermined constant, then so is
2C. So why bother with the 2)
Remember the sum rule for derivatives? It is that the derivative of a sum is the sum
of the derivatives. Can you see how this would work for indefinite integrals as well?
If F(x) is an antiderivative of f(x), and
G(x) is an antiderivative of g(x), then
it is always true that
|

|
(f(x) + g(x)) dx = F(x) + G(x) + C eq. 11.2-13a
|
|
Or in other words, the indefinite integral of the
sum is the sum of the indefinite integrals. Another way to
put this is
|

|
(f(x) + g(x)) dx =
|

|
f(x) dx +
|

|
g(x) dx eq. 11.2-13b
|
|
Not only that, but just as equation 11.2-13b breaks an integrand that is the sum of two things into the
sum of two integrals, if the integrand is the sum of three things, you can break it into the sum of
three integrals. Indeed if it is the sum of n things, you can break it into the sum of n
integrals.
In the table that follows you can see that we have essentially taken the table
from the section on derivatives and turned it around. It is useful to know these indefinite integrals
at a glance, so consider memorizing this (which should be easy if you have already familiarized
yourself with the table of derivatives). These together with the rules we covered above
will form the core of knowledge you need in more
complex integration problems after you have applied other tools to the integrand.
Table 11-1: Indefinite Integrals of some Common Functions
function indefinite integral
|

|
dx x + C
|

|
1
x dx x2 + C
2
|

|
1
xs dx [s ¹ -1] xs+1 + C
s+1
|
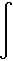
|
dx
=
x
|
|
1
dx ln|x| + C
x
|
|
dx
=
xs
|
|
1 1 1
x-s dx [s ¹ 1] - + C = x1-s + C
s-1 xs-1 1-s
|

|
_ 2 _ 2
Öx dx [same as xs with s = 1/2] xÖx + C = x3/2 + C
3 3
|

|
ex dx ex + C
|

|
cos(x) dx sin(x) + C
|

|
sin(x) dx -cos(x) + C
|
Be sure you understand how we arrived at all the indefinite integrals in the table above.
These are the ones you can infer simply by knowing the derivatives of some elementary
functions.
The goal of all the other methods
we will learn from now on will be to reduce the problem of taking the indefinite
integral to one or more of the integrals in this table. It is also very
useful for you to memorize equation 11.2-11b and
equation 11.2-13b. They form your first shelf of tools
for reducing an indefinite integral problem into an entry on the table.
Exercises
Find the indefinite integrals of the following (and don't forget to add the undetermined
constant on each one. Most instructors mark you down a point or two if you
leave that out. And don't forget to check your answers by taking the
derivative of the function you ended up with and matching that back to
the original integrand):
|
1) 
|
______
Ö3x + 2 dx
|
See solution
|
2) 
|
(sin(px) + cos(3px)) dx
|
See solution
|
3) 
|
2
+ e-nx dx
1-x
|
where n is a constant.
Notice that on this one the integrand is a sum, but there are no parentheses
enclosing it before you get to the dx. Many books will write it this way
because the integral is assumed to be over everything between the integral sign
and the dx, even if you leave the parentheses out.
See solution
|
4) 
|
x4 + 8x3 + 12x2 - 4x - 3 dx
|
See solution
|
5) 
|
n
å Bk(kx + 1)k dx
k=1
|
where each Bk is a constant. This problem is shown in a funny color because
it is intended to challenge you. So consider it extra credit. But keep in mind that everything
you need to know in order to do this problem is on this page of the tutorial. Don't let the
summation sign scare you. The rule given in equation 11.2-13b applies to
sums even when they are shown using the sigma notation. Your answer will have to use the
sigma notation as well. Use the rule given in 11.2-11b to integrate
the expression inside the summation. You can treat k as a constant for the purposes
of the rule, because k does not vary with x.
Your answer will be the summation of whatever you end up with after applying the
rule and taking the integral.
See solution
Long ago in a galaxy far away...
the technological terror known as the Death Star aimed its
weapons at the peaceful planet,
Alderaan,
and, just for jollies, shattered it into countless fragments that
still drift endlessly through the universe to this very day. You
probably recall the exact scene of Alderaan's destruction from the movie,
Star Wars.
Surely the Death Star had enormous energy resources at its
disposal. But the question that was undoubtably gnawing at the minds
of many a viewer after having seen the movie was, "Exactly
how much energy does it take to fragment an entire planet?"
Well thanks to what you've learned in last few sections, along
with a little basic physics that I will tell you now, you
have become equipped to answer this mystery.
The basic physics is this: The energy required to lift an object
of mass, m, from the surface of a planet of mass, M,
to a point where it is free of the gravity of that planet is
GMm
E = eq. 11.2-14
r
where r is the radius of the planet, and G is
the universal contant of gravity. If you measure mass in kilograms,
distance in meters, and energy in watt-seconds, then
G = 6.7 × 10-11 watt-second-meters per kg2
(from Astronomy Data Book by J. Hedley Robinson).
Here's how we figure it. Imagine that you have a perfectly spherical
planet. For simplicity we shall assume that its mass density is uniform
all the way through, with a value of
r kilograms per meter3.
We will use the physics formula to figure out how much energy it takes to remove a very
thin shell of the planet from its surface and free it from the planet's gravity.
Let the thickness of the shell be dr. Then the volume of the shell
(not the volume enclosed by the shell, but the volume sandwiched between the outer
and inner surfaces of the shell) will
be very nearly the surface area of the planet times the thickness, dr
(the thinner the shell, the more accurate this estimation of its volume is). The mass of
that shell, dm, will be r times the shell's
volume. Since we know the surface area to be
A = 4pr2,
dm = 4pr2r dr eq. 11.2-15a
We also know that the planet's mass is its volume times its density. The volume
we know from
V = (4/3)pr3.
So we have
4
M = pr3r eq. 11.2-15b
3
If you put the expressions for M and for dm into the physics formula
given in equation 11.2-14 and gather the terms, you find that the energy, dE, needed to remove
the thin shell of thickness dr from the planet is:
16G
dE = p2r4r2 dr eq. 11.2-15c
3
Of course once you have removed the outer shell, the planet is just a wee bit smaller.
In other words, r is just a little less. To know how much energy we need
to remove all of the planet's volume, we need remove thin shell after thin shell,
until we get down to nothing, and we need to add up all the dE's that result.
That is where integration comes in.
If E(r) is the amount of energy that it takes to dismember a planet
of radius, r, then
dE = E(r) - E(r - dr) eq. 11.2-16
This equation helps us get our signs right when we do the definite integral.
It shows that we need to take the energy function of the larger radius
minus the energy function of the smaller radius. In other words, we will
take the definite integral from the smaller radius to the larger radius.
But what is the energy function? Doesn't adding up all those dE's
look a whole lot like taking a Riemann sum? So we do it by taking the integral.
Remember that the volume of the shell in equation
11.2-15a was only an approximation?
But the integral takes the limit as the shell's thickness, dr, goes to zero.
And that in that limit, the approximation is perfectly accurate.
Since we are taking the sum over a bunch of different r's, the
independent variable that we integrate over must be r. The indefinite
integral of equation 11.2-15c is
E(r) =
|

|
16G
p2r4r2 dr eq. 11.2-17a
3
|
But 16/3, G, p, and
r are all constants.
By the rule established in equation 11.2-3, the above integral is the same as.
16G
E(r) = p2r2
3
|

|
r4 dr eq. 11.2-17b
|
We've seen this form of integral before in equation 11.2-4f. Applying
that formula to this we get
16
E(r) = G p2r2r5 + C eq. 11.2-17c
15
This, remember, is only the indefinite integral.
We determined earlier that we have to take the definite integral from
the smaller radius to the larger radius. Since we want to dismember the entire
planet and have nothing left when we are done, the smaller radius is zero.
And since we start with the entire planet, the larger radius is the radius
of the undisturbed planet, which I will call rA for the
radius of Alderaan.
rA
E =  0
0
|
16G
p2r2r4 dr =
3
|
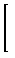
|
16
Gp2r2r5
15
|
rA
 0
0
|
16
= Gp2r2rA5 eq. 11.2-18
15
|
Instead of carrying around all those symbols, we can use equation 11.2-15b
to simplify the expression we have on the right. That equation gives us the mass of the planet as
a function of r. If we square both sides of 11.2-15b we find that
16
M2 = p2r6r2 eq. 11.2-19a
9
9 M2
= 1 eq. 11.2-19b
16 p2r6r2
If MA is the mass of Alderaan and rA is its
radius, the above becomes
9 MA2
= 1 eq. 11.2-19c
16 p2rA6r2
Since you can multiply anything by one and not change it, I will multiply the right
side of equation 11.2-18 by the form of one that we have here in equation 11.2-19c.
We get lots of good cancellations that way (getting rid of the
p2 and the density and leaving
us with a simple expression in terms of radius and mass):
3 GMA2
E = eq. 11.2-20
5 rA2
This gives you the energy that the Death Star had to deliver in order to
blow up Alderaan. I don't happen to know the mass or radius of Alderaan,
but since I have always been deeply concerned that the Death Star might
show up some day and smash our beautiful world, I have worked the numbers
for the earth. From Astronomical Data Book by J. Hedley Robinson:
Me = 6.0 × 1024 kilograms (mass of the earth)
re = 6.4 × 106 meters (radius of the earth)
My calculator tells me that for the earth, E = 2.3 × 1032 watt-seconds.
To give you some idea of how much energy that is, the total radiated output
of the sun (not just what falls on the earth, but what goes off in all directions
into space as well) is 3.9 × 1026 watts.
So it would take about 590,000 seconds for the sun to radiate that much
energy. That's about 4 hours short of a week. Looking at
it another way, according to Einstein's famous equation,
E = mc2, (where c
is the speed of light, about
3 × 108 in meters per second), the Death Star would have
to convert 2.5 trillion tons of matter completely to energy in order
to destroy the earth. I doubt if the Death Star even weighs that much.
What it boils down to is that the numbers having to do with things
astronomical (such as gravitational binding
energy of a planet) are -- well -- astronomical.
I hope that puts your mind at ease. The earth is way too tough a planet
for the Death Star. So stuff that into your shiny black helmet, Darth Vader.
Section 11.2: Not Available Yet
Return to Table of Contents
hahn@netsrq.com


