In the last section we saw that if we know the derivatives of a pair of functions, then we can quickly find the derivative of their sum, difference, or product. We also saw that we can quickly find the derivative of a constant times any function whose derivative we already know. But we still haven't covered all the ways to combine functions.
I have no cute stories about animals or animated tattoos for quotients. Fortunately, they are easy once you know the product rule. So here is a straight-ahead explanation.
In the answer to exercise 3 of section 4.2 we turned a difference into a sum so that we could derive a difference rule from the sum rule. Here we shall turn a quotient into a product to derive a quotient rule from the product rule. We would like to know the derivative of:
f(x)
h(x) = eq. 4.3-1
g(x)
Simply by multiplying both sides of 4.3-1 by g(x), we turn the
problem around to:
h(x) g(x) = f(x) eq. 4.3-2These two equations, 4.3-1 and 4.3-2, say exactly the same thing, don't they? But in 4.3-2 we have a product on the left and no quotient anywhere. And we already know how to take the derivative of a product. So by applying the product rule to the left hand side of 4.3-2 and simply taking the derivative of the right hand side (remember, if two things are equal, their derivatives are equal as well) and we get:
(h'(x) g(x) ) + (h(x) g'(x) ) = f'(x) eq. 4.3-3All we have to do to finish this derivation is get h'(x) by itself over on one side of the equation and everything else onto the other side. If you subtract
h'(x) g(x) = f'(x) - (h(x) g'(x) ) eq. 4.3-4Now you can divide out g(x) from both sides to isolate h'(x) over on the left:
f'(x) - (h(x) g'(x) )
h'(x) = eq. 4.3-5
g(x)
And this would be a suitable answer, except that we'd like the right
hand side of 4.3-5 to be in terms of f(x), g(x),
f'(x), and g'(x) only. In 4.3-5 we see that h(x)
term on the right hand side. But it's easy enough to get rid of. We
have an expression for h(x) in 4.3-1. Simply by substituting
we get:
æ f(x) ö
f'(x) - ç g'(x) ÷
è g(x) ø
h'(x) = eq. 4.3-6
g(x)
Your algebra instructor would probably have you simplify this by multiplying numerator and denominator by g(x).
(g(x) f'(x) ) - (f(x) g'(x) )
h'(x) =
|
(where g2(x) indicates the square of g(x)). And this (equation 4.3-7) is the quotient rule whenever
f(x)
h(x) =
g(x)
In words, the derivative of the quotient is the denominator times the
derivative of the numerator minus the numerator times the derivative
of the denominator all over the denominator squared.
You can also go to a lot more trouble to derive this same rule using the limit method we used to derive the sum and product rules, but why bother when you can derive it using an existing rule and a little old fashioned algebra? But some instructors, for reasons known but to themselves, will ask you on an exam to derive this thing the hard way. So if you need to learn the hard way, click here. As far as I'm concerned, though, math is about doing things the easiest way you can find.
Find the derivative of:
x + 1
h(x) =
x - 1
We can see that this is the quotient of
( (x - 1)(1) ) - ( (x + 1)(1) )
h'(x) =
(x - 1)2
When you gather up like terms in the numerator, you end up with:
-2
h'(x) =
(x - 1)2
|
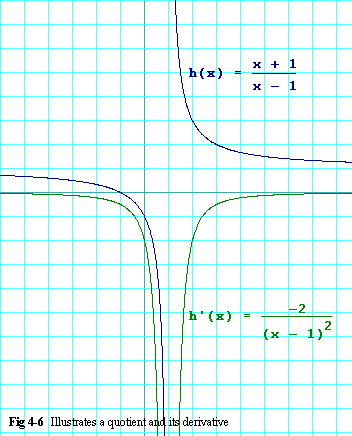
Figure 4-6 shows both h(x) and h'(x) in this example.
Observe the graph carefully. Notice that h(x) (the blue trace)
always slopes down. Correspondingly, h'(x) (the green trace) is
always negative. At the extreme right and left of the graph, the blue
trace shows us that h(x) flattens out. In fact its limit as
x goes toward either infinity or -infinity is
1. Correspondingly, as the blue trace flattens out, the green
trace shows us that h'(x) gets close to zero. We expect that
because "flattening out" means that slope is getting close to zero.
And most importantly,
we know that at |
|
We have seen by two separate proofs that if
Recall from algebra that when we say
1
h(x) = eq. 4.3-8
xn
This is something we can apply the quotient rule to.
If n is a counting number, then -n is a negative
integer.
Let
(xn × 0) - (1 × nxn-1)
h'(x) = eq. 4.3-9
x2n
The left hand half of the numerator goes away because it is multiplied
by zero. The right hand half is multiplied by 1. So 4.3-9
simplifies to:
-nxn-1
h'(x) = eq. 4.3-10
x2n
You can see that we have a multiple of a power of x in the
numerator, and a power of x in the denominator. Recall from
algebra that the way we divide x to one power by x to
some other power is by subtracting the smaller exponent from the bigger one.
If the numerator's exponent was bigger, then the resulting term goes
into the numerator and the x to the power term in the denominator
cancels. Likewise, if the denominator's exponent was bigger, the resulting
term goes into the denominator and the x to the power term in
the numerator cancels. Here we have the latter case. So applying that
algebra rule we have:
-n
h'(x) = eq. 4.3-11
xn+1
But when we have an exponential term in the denominator, our negative
exponent rule from 4.3-8 says we can use a negative exponent to write
it:
f'(x) = -nx-n-1 eq. 4.3-12Look at the rule we have for taking the derivative of xn and see how 4.3-12 is the same thing, only with a negative exponent. That is, if you substituted -n for n into xn and applied the rule for taking the derivative of xn, wouldn't you get precisely the expression in 4.3-12 (which we derived using the quotient rule and some algebra)? That is why the rule for taking the derivative of xn works even when n is a negative integer.
1) Find the derivatives of the following:
x2 + 2x + 1
a) h(x) =
x2 - 3x + 2
x (x - 3)
b) h(x) =
x2 + 1
c) h(x) = 3x-3
f(x)
d) h(x) =
x3 - 4x2 + 3x - 1
x2
e) h(x) =
g(x)
1
f) h(x) =
x-2 - x-1
1
g) h(x) =
f(x)
2) Look at the answer to problem 1g. What rule can you establish about
taking the derivative of the reciprocal of a function? (hint: If you did
1g you already have the answer).
3) We know from algebra that if
f(x)
h(x) =
f(x)
then We have already learned how to take the derivative of pairs of functions combined by any of the four arithmetic operations. You have known those four operations since you were in grammar school, so once understand what a derivative is, it was fairly easy to understand what the sum or product or quotient rules were trying to say. Each one said, "If you have two functions combined by this arithmetic operation and you want to know the derivative of the combination, then apply the following rule:" And each one went on to prescribe some arithmetic munging of the two functions and their derivatives that, if you did that munging, you'd end up with the derivative you were after.
In grammar school, they didn't teach you about composites. That's because you can't take the composite of two numbers, only the composite of two functions. But now you know that the composite of two functions is the same as applying both functions, in succession, to some value.
So, for example, if
_
f(x) = Öx
and
______
f(g(x)) = Ö1 - x2
Notice that
this is simply applying g to x, and then applying f
to the result. Notice also that if you applied f first, then
g, you'd get a different result. In math-speak, we say that
composition is noncommutative, meaning that order of application
matters.
Because composition of functions is something you didn't study until recently, you may have more difficulty with the concept than you do with addition, subtraction, multiplication, or division. Here is an everyday analogy. When you bake bread, you knead the dough. Think of that as a function. The dough is changed by kneading it. Then you let the kneaded dough rise. That is another function that causes a change in the dough. Once you have kneaded the dough and let it rise, you have performed a composite function on the original dough. And notice that the order in which you performed these functions matters. If you let the dough rise before you knead it, you would end up with something less than bread. Of course there is another function that you must combine with kneading and rising to get bread, and that is baking. So bread is made by a composition of three functions on the dough. And only one order of applying those three functions works to make bread. Any other order makes something, but not many folks would want to eat it.
There is one more concept involving composites that it is useful for
you to know, and that is the idea of functions that are inverses of each
other. If f(x) is the inverse of g(x), then
If f(x) is the inverse of g(x), then we typically
write
An example of inverse functions is
Some functions are their own inverses. For example,
C
f(x) =
x
is its own inverse whenever C is any constant other than zero.
If you apply this function twice to any x other than
In section 3.1, we had a little story about the professor's abberant watch. This watch, though set at noon to match the station clock, would sometimes run fast and surge ahead of the station clock. Other times it would run slow and straggle behind the station clock.
The professor's watch never stopped, ran backward, or skipped ahead. We gave the name, t, to the time on the station clock and tp to the time on the professor's watch.
You will recall that the professor understood well the idiosyncrasies of
his watch. He understood them well enough that he could infer the
station clock time by looking at his watch. He knew that for any
time, t, that the station clock showed, there was a unique time,
tp, that his watch would show at that same time.
Hence, he knew what function it was that mapped t into
tp. We gave that function a name. We said
But knowing the function, w(t), cannot tell you or the professor
the station clock time by reading the watch. It can only tell you the
watch time knowing the time on the station clock. To know the station
clock time from the watch time, we and the professor have to know
what the inverse of w(t) is. That is we want
Figure 4-7 shows w(t), w-1(tp),
and both of their derivatives.
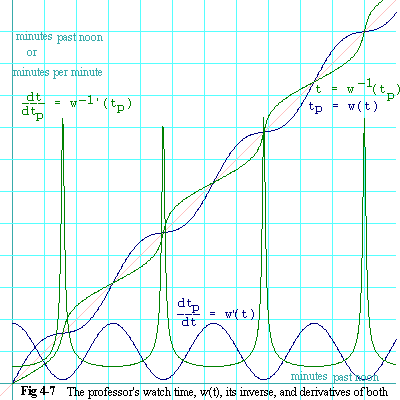Let's begin by looking at w(t), which is the blue trace that
ramps up from lower left to upper right in a wavy pattern. When looking
at this trace, the horizontal axis is the station clock time, t,
and the vertical axis is the professor's watch time, tp.
Both axis start at noon. You can see that at noon, the professor's watch
also reads noon. But his watch is gaining time, and within a minute,
the professor's watch is almost half a minute fast. Then the
professor's watch begins to lose time. At about 12:01:34, the professor's
watch once again agrees with the station clock. But his watch continues
to lose time. Within another minute, the watch is running about half a
minute behind the station clock, but now the watch begins gaining back
some time. At about 12:03:08, the professor's watch once again agrees
with the station clock, but continues to gain time, and the cycle starts
over again.
Notice there is a pink trace on the graph that goes up in a straight line. Each time the blue trace, w(t), crosses the pink, the professor's watch momentarily agrees with the station clock.
There is a second blue trace that traverses the bottom of the graph horizontally in a wavy pattern. This is the derivative of w(t). Again, the horizontal axis it the station clock time. The vertical axis, in this case is the rate at which the professor's watch advances as a fraction of the station clock time.
At noon (extreme left) we see that the professor's watch is going at a rate of about 1.88 minutes forward for every minute the station clock goes forward. In other words, the professor's watch is running about 88% fast. At about 47 seconds past noon, the professor's watch is running at one minute for every minute on the station clock. In other words, at that moment, the professor's watch is running at the right speed, even though it reads half a minute ahead of the station clock. But at 12:01:34, the professor's watch is running at only 12% the rate of the station clock, that is, the professor's watch only advances 0.12 minutes for every minute the station clock advances. To put in another way, at that moment, the station clock is running about eight times as fast as the professor's watch. Of course, shortly after that, the professor's watch begins to speed up again, and at about 12:02:21, it is running at the same rate as the station clock, although it is still behind for having run so slow in the minute and a half just past. After that, the professor's watch continues to speed up until (at 12:03:08) it is once again running 1.88 minutes for every minute on the station clock. And then the cycle repeats itself.
Now to the green traces. The wavy green trace that ramps up from lower left to upper right is w-1(tp). So it represents what the station clock reads knowing the time on the professor's watch.
When interpreting this trace, the horizontal axis is the time shown on the professor's watch, tp, and the vertical axis is the station clock time, t. Recall that at noon, the professor's watch was gaining time on the station clock. Looking at that another way, the station clock was losing time on the professor's watch. So when the professor's watch shows 12:01 (one square to the right of the vertical axis), the station clock shows only about 12:00:33. But by 12:01:34 on the professor's watch, the station clock has gained on the professor's watch to the point that they agree again. This is not because the station clock has sped up, but because the watch has slowed down. But if you were keeping time by the professor's watch, the station clock would have appeared to have sped up.
The station clock continues to outpace the professor's watch for just a short while, then begins to drop back relative to the watch, until they agree again at about 12:03:08. Then the cycle begins again.
The green spiky-looking trace is the derivative of w-1(tp). Again, when interpreting this trace, the horizontal axis is minutes on the professor's watch. The trace shows the rate at which the station clock appears to run to an observer who keeps time by the professor's watch. Recall that when the professor's watch ticks at its slowest rate, it is going only 12% the rate of the station clock. Or looking at it another way, the station clock is, at that moment, running about eight times as fast as the professor's watch. And you can see that the spikes come right up to about 8 minutes that the station clock ticks off per minute that the watch ticks off.
Recall that in section 3.1, we were interested in the train's position as a function of time, and particularly as a function of time as measured by the professor's watch. The train's position as a function of the station clock time we shall call x(t). It's position as a function of professor's watch time we shall call xp(tp). And remember we came up with the relationship:
xp(tp) = x( w-1(tp) ) eq. 4.3-13You can see that the right hand part of 4.3-13 is a composite of the two functions, xp and w-1. And what the right hand side says is, "to find the position of the train as a function of the professor's watch time, first find the station clock time from the professor's watch time using w-1, then apply the function, x(t), that gives you the train's position as a function of station clock time."
Figure 4-8 shows the train's position as it leaves the station as a function
of station clock time in blue and as a function of the professor's watch
time in green.
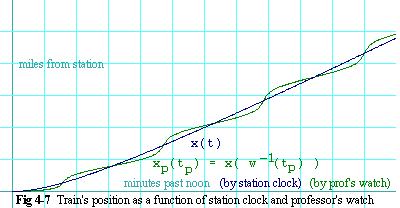Observe that as the train leaves the station at noon, the professor's
watch is outrunning the station clock, or in other words, the station
clock is falling behind the professor's watch. So according the professor's
watch, the train is not going as fast as it would be going by the station
clock. Later, the station clock surges ahead of the professor's watch.
When the station clock appears to be gaining time on the professor's
watch, the train appears, by the watch, to be going faster than it does
by the station clock. In fact, knowing that the speed of the train by
the professor's watch is the slope of the green curve, we can see that
the train appears to be going quite a bit faster during the surge than
the speed as measured by the station clock. Perhaps even 8 times
as fast?
And that is the point this whole story has been leading to. If
the train moves at half a mile per minute by the station clock, how fast
is it going by the professor's watch at the moment the watch is running
slow by factor of 8? In that brief time, with each second ticked
off by the professor's
watch, the station clock ticks off 8 seconds. And the train
moves
And what function is it that we have already seen that goes up by a factor
of eight during that brief moment? It's
w-1'(tp) (see figure 4-7). Figure 4-9
shows the speed of the train as a function of time according to both
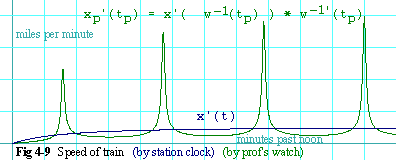the station clock (blue) and the professor's watch (green). We can see
that according to the station clock (which is the accurate timepiece here),
the train accelerates smoothly from the station and settles at a steady
speed of 0.5 miles per minute (30 miles per hour). But
by the professor's watch, the train appears to surge momentarily to nearly
4 miles per minute (240 miles per hour) every 3
minutes and 8 seconds, or thereabouts.
Now recall that speed is the time derivative of position. So the two traces on figure 4-9 are x'(t) (blue) and xp'(tp) (green). That is, they are the derivatives of x(t) and xp(tp) respectively. And recall also that xp(tp) is a composite of x'(t) with w-1(tp), as shown in equation 4.3-13. So it seems that we have uncovered a rule for finding the derivative of a composite function.
In the example suggested by the story, we found the derivative of the
composite,
|
And that is The Chain Rule. If you have: h(x) = f( g(x) ) eq. 4.3-14athen h'(x) = f'( g(x) ) g'(x) eq. 4.3-14b |
Here is an example. Suppose
h(x) = (x2 + 1)3 eq. 4.3-15aThere are two ways we can find the derivative of this. One is to multiply it out and use the rules we have already established. The other is to apply the chain rule. To apply the chain rule, we observe that if
f(x) = x3 eq. 4.3-15band
g(x) = x2 + 1 eq. 4.3-15cthen
f'(x) = 3x2 eq. 4.3-15dand that
g'(x) = 2x eq. 4.3-15eHence we have
f'( g(x) ) = 3(x2 + 1)2 eq. 4.3-15f(make sure you understand how I got that by substituting 4.3-15c for x into 4.3-15d)
Equation 4.3-15f does step one of the chain rule, which is making the substitution into the derivative of the outer function of the composite. The second step says to multiply the result of the first step by g'(x), that is by the derivative of the inner function of the composite. So from 4.3-15e and the chain rule, we have
h'(x) = 3(x2 + 1)2 (2x) eq. 4.3-15g
I mentioned at the beginning of this example that there are two ways of doing it. And you'd expect that they both arrive at the same answer. The second way of doing it is to multiply out 4.3-15a and find the derivative of the result. When you multiply out 4.3-15a, you get
h(x) = x6 + 3x4 + 3x2 + 1 eq. 4.3-16aand taking the derivative of the sum, term by term, we have:
h'(x) = 6x5 + 12x3 + 6x eq. 4.3-16bIf you use a little algebra and factor a 3 and a 2x out of 4.3-16b, you get
h'(x) = 3(x4 + 2x2 + 1) (2x) eq. 4.3-16cFinally if you use a little more algebra, you notice that
h'(x) = 3(x2 + 1)2 (2x) eq. 4.3-16dwhich is the same expression as in 4.3-15g. So the chain rule comes up with the same answer as the methods we already know in this example. Can we be sure it will come up with the right answer all the time? Here is the proof that it will (and this might be on an exam):
We know that the derivative of an arbitrary function, u(x), is defined by
u(x + h) - u(x)
u'(x) = lim eq. 4.3-17
h > 0 h
(here I have used u(x) in place of h(x) so that it does
not get confused with the variable, h)
If u(x) is the composite,
f( g(x + h) ) - f( g(x) )
u'(x) = lim eq. 4.3-18
h > 0 h
Using the same substitution that we used to derive the sum and product rules,
that is that in the limit,
f( g(x) + h g'(x) ) - f( g(x) )
u'(x) = lim eq. 4.3-19
h > 0 h
Think about the term,
To make things easier to decipher, let's make up two new variables,
h* = h g'(h) eq. 4.3-20aand
x* = g(x) eq. 4.3-20bIf we substitute them into 4.3-19 we get:
f( x* + h* ) - f( x* )
u'(x) = lim eq. 4.3-21
h > 0 h
Using the same principle as we used to substitute for
f( x* ) + (h* f'( x* ) ) - f( x* )
u'(x) = lim eq. 4.3-22
h > 0 h
Taking the cancellation we have:
h* f'( x* )
u'(x) = lim eq. 4.3-23
h > 0 h
Now simply substitute back to the original variables, h and x
using 4.3-20a and 4.3-20b to get:
h g'(x) f'( g(x) )
u'(x) = lim eq. 4.3-24
h > 0 h
Then using our old friend, the rule from
section 2.5, we can take the limit and find that
u'(x) = g'(x) f'( g(x) ) eq. 4.3-25And thanks to the commutativity of multiplication, this is the same as what we stated as the chain rule earlier.
Your instructor might have used an approach more similar to what follows than to what I just gave above. Look at the following proof, and if it seems more familiar to you than the above, then it is the one you should reproduce on an exam if asked.
We start again with the limit formula. If
f( g(x + h) ) - f( g(x) )
u'(x) = lim eq. 4.3-26
h > 0 h
Whatever the difference between g(x + h) = g(x) + k eq. 4.3-27and we substitute that into equation 4.3-26 to get
f( g(x) + k ) - f( g(x) )
u'(x) = lim eq. 4.3-28
h > 0 h
Now multiply numerator and denominator by k/h.
f( g(x) + k ) - f( g(x) ) k
u'(x) = lim eq. 4.3-29a
h > 0 k h
It's clear that when h goes to zero, k must also
go to zero. So under the lim sign, we can replace h
with k
f( g(x) + k ) - f( g(x) ) k
u'(x) = lim eq. 4.3-29b
k > 0 k h
We know that
f( g(x) + k ) - f( g(x) )
f'(g(x) ) = lim eq. 4.3-30
k > 0 k
Why? Because this is the limit formula for that derivative, except that
h has been replaced with k and x has been
replaced with g(x). So, substituting, equation 4.3-29 becomes
k
u'(x) = lim f'(g(x) ) eq. 4.3-31
k > 0 h
All that remains is to find out what k/h is. Well the formula
for g'(x) is
g(x + h) - g(x)
g'(x) = lim eq. 4.3-32
h > 0 h
but remember from equation 4.2-27, we had
g(x) + k - g(x)
g'(x) = lim eq. 4.3-33
h > 0 h
and we get cancellation of the g(x)'s here:
k
g'(x) = lim eq. 4.3-34a
h > 0 h
As stated before, whenever h goes to zero, k
must also go to zero. That means that under the lim sign, we
can replace h with k.
k
g'(x) = lim eq. 4.3-34b
k > 0 h
So where k/h appears in equation 4.3-31, we
can substitute g'(x).
u'(x) = lim f'(g(x) ) g'(x) eq. 4.3-35
k > 0
And since k doesn't appear anywhere to the right of the lim
sign, that means the expression to the right of the lim sign is
its own limit. So we have
u'(x) = f'(g(x) ) g'(x) eq. 4.3-36which is what we set out to prove.
The
Leibniz "d" notation makes it
easy to remember how to apply the chain rule. Remember that the Leibniz
notation always shows what variable a derivative is taken with respect to.
We want to find the derivative with respect to x of
dg
g'(x) = eq. 4.3-37a
dx
and
df
f'(g(x)) = eq. 4.3-37b
dg
Notice that in the latter equation, g is treated as a variable
rather than a function. Actually it is both. Indeed, as you move on
to more advanced calculus you will find that in many situations something
is both a function and a variable. So in equation 4.3-37b we are taking
the derivative of f with respect to g, and g
is a function of x. This is because when you take
f'(anything) you get the derivative of f with
respect to that particular anything. In this case,
the anything is g(x), or simply g.
What we are interested in finding is the derivative of f with respect to x, which, in the Leibniz notation is
dfWe can finddx
dg dfusing equations 4.3-37a & b respectively. Now look what happens when we multiply them together:anddx dg
df dg dfJust as Leibniz envisioned, we can treat the ratios of the "d" quantities as if they were fractions and cancel "d" quantities that match in the numerator and denominator. So dg in the denominator of the first factor cancels the dg in the numerator of the second factor. When you substitute back from equations 4.3-37 a & b, you getdgdf==eq. 4.3-38 dg dxdgdx dx
df dg dfIf you use the Leibniz notation to check your use of the chain rule, it will never steer you wrong. When the cancellations get you the derivative you are interested in with respect to the variable you are interested in taking it, then you have used the correct chain rule product.= f'(g(x)) g'(x) =eq. 4.3-39 dg dx dx
Move on to Chain Rule Applications
email me at hahn@netsrq.com