

If you want to drive along Interstate 95 from the George Washington Bridge to the Connecticut state line, you must pass through a sliver of Manhattan, then a trek through The Bronx, then Pelham Manor, then New Rochelle, then Larchmont, then Harrison, then Rye, and finally through Port Chester. When you are almost through New Rochelle, you can't simply decide, "I never liked Larchmont, so let's just skip it," and jump through to Harrison (which would, coincidentally, save you a buck at the toll plaza). If you stay on I95 from the bridge to Connecticut, you must visit all the places in between.
Likewise, if your 20,000 gallon swimming pool starts out empty, and you begin filling it, there will be a moment when it contains exactly 5,673 gallons. There will be another moment when it contains exactly 12,891 gallons. No matter what number of gallons you name between zero and 20,000, there will be a moment when your pool contains exactly that many gallons. It doesn't matter how hard you turn on the hose, or how many times you adjust the valve. You just don't get to skip any numbers, no matter how unlucky your numerologist says they are.
Just one more example -- the rubber-burning monster of a sports car you just bought can go from 0 to 60 mph in 6.9 seconds. But it can't get you from 0 to 60 without at some time taking you through all the speeds in between.
All of the above are examples of nature's tendency to be continuous. Nature doesn't like instantaneous changes or perfectly sharp edges. Nature wants things to happen smoothly. Even something as abrupt as the shock wave of an explosion does not happen instantaneously, but builds up over a period of time, though that time be measured in microseconds.
We can talk about real valued functions of a real variable in the same
way. We have a sense about functions like
These notions are useful for getting an idea of what continuity is all about, but they lack the rigor we need to do mathematics with them. There simply is no mathematical definition of smooth or sharp or of a pencil. Fortunately, the concept of limits, as we have developed it so far, gives us the perfect tool to nail down the notion of continuity.
First notice that continuity is a local property. If Interstate 95 has a bridge that is out, then we would like to say that it is continuous everwhere except at the missing bridge. The same is true when we talk about functions.
Suppose we define the function,  You can define it to be whatever you like
at
You can define it to be whatever you like
at
So what is it that's happening to u(x) everwhere except at
lim u(x) = u(a) eq. 3.0-1 xAt every> a
The function,
But first, let me answer a few questions that curiosity may be stuffing
into your head
at this very moment. In the example of u(x) we saw a function that
was continuous everywhere except at one point. Is there a function that is
continuous everywhere except at several points? Yes. Is there one that
is continuous
everywhere except at infinitely many isolated points? Yes. Is there one
that is
continuous nowhere at all? Yes. Is there one that is continuous only at
a single point? Yes. Is there a function that is continuous everywhere
yet cannot be graphed? Yes. And later on I shall give you examples of
all of these.
But now let's get back to our analysis of
lim x2 = a2 eq. 3.0-2 xand we say that this holds for any a you might choose. We can state the contract version of this just by applying the contract version of our definition of what a limit is. So the contract version is: whatever real number, a, you might name and whatever> a
|x2 - a2| £ e eq. 3.0-3whenever
But can we prove that 3.0-2 holds for all a using the contract?
Let
|(a + error)2 - a2| £ e eq. 3.0-4whenever
|2a error + error2| £ e eq. 3.0-5whenever
Can we choose error
so that 3.0-5 always holds? Certainly. Just choose error so that
it is the lesser of
That works for all a, except zero.
But when
So now you have a recipe for finding error given e and a. Just make d the same as the error we chose in the previous two paragraphs, and you have a recipe for finding d given e and a. And that is what the contract said we should be able to do. Not only that, but it works for any a.
You are likely to be called upon on an exam to prove continuity of some
function using the method just detailed, or one similar to it. Read over
the discussion of why
So what about the first function we looked at, our friend, u(x)? If it really is continuous everywhere except at zero, then our limit test should pass everwhere except at zero, and there it should fail.
Our contract for u(x) is: for any
|u(x) - u(a)| £ e eq. 3.0-6whenever
Whenever a is not zero, we can always find a d small enough so that the interval that extends out a distance d on each side of a does not include zero. You can see this graphically on a number line.
0 < d >a< d >
--------------------------|-------[---------------+----------------]-------
fig. 3-2
No matter how close a is to zero, you can clearly pick d
small enough so that the interval shown in the diagram does not include zero.
So let's pick such a d. And when we do that, we get another
effect. The entire interval is
on the same side of zero -- that is you don't have one part of the interval
on the positive side of zero and the other on the negative side.
Well, whenever x is inside
the interval shown, it is certainly true that
|x - a| £ d Û x is in the interval eq. 3.0-7And since the entire interval is on the same side of zero, u(x) is certainly constant throughout the interval. That is, if the interval is entirely on the positive side (as shown in the diagram), then
That means that whenever
But what about when
Some candidates we might pick for u(0) are 0, 1, or anything in
between. It turns out, it doesn't matter. You can pick any real number
you like and say that that is what u(0) equals, and the contract
will still fail at
At
< d >0< d >
-----------------------[-----------|-----------]---------------------
fig. 3-3
Again, x being in the interval is the same as
|x| £ d Û x is in the interval eq. 3.0-8There simply is no way to exclude zero from this interval. More important than that, the interval must exist on both sides of zero -- that is some of it must be on the positive side and some of it must be on the negative side. This is true no matter how small you pick d.
So if you told me that you wanted u(0) to be 0, then there are
values of x in the interval shown for which
|u(x) - u(0)| = 1 eq. 3.0-9That means that if you choose any
Similarly, if you say that
And suppose you pick u(0) to be something that isn't 0 or 1? Well,
let's do that. Let's call it y.
We still have a problem.
y is different from any u(x) when x is on the
positive side of the interval (where
I just can't win, no matter what I choose for u(0). The contract
always fails. And that's why u(x) cannot be continuous at
We began this discussion with the metaphor of a highway, and that to
get from point A to point B on a highway, you have to visit all the
points in between. We went on to use a definition involving limits
to define what continuity of a function is. Specifically, we stated
that a function f(x) is continuous at
f(a) = lim f(x) eq. 3.0-10
x > a
But we never made the connection from the definition to the
points-in-between concept.
The intermediate value theorem makes that
connection. It says that if you start at a and travel to b,
visiting all the points in between, then for a continuous function,
f(x), it must travel from f(a) to f(b) and
must visit all the points in between f(a) and f(b).
The usual statement of the intermediate value theorem is: if f(x)
is continuous on the closed interval,
Read that statement of the intermediate value theorem over several times and make sure you understand what it means. You are likely to be tested on it. Try to see why the theorem implies, among other things, that if
f(x) = x2is continuous everywhere and
Think of it this way. If you take a pencil to paper and begin drawing a mark always moving from left to right, but while you do that you also move the pencil-point up and down, and you never pick the pencil-point off the paper, what can you say about the mark you made? If you made it to the top of the page anywhere, and you made it to the bottom of the page anywhere, then you made it to all the heights in between. It's just common sense.
In fact, the intermediate value theorem seems intuitively obvious until
somebody comes along and says, "If it's so obvious, then prove it."
It is then that you realize that its everyday applications to our
experiences in life are obvious, but a rigorous proof is another matter.
The proof is not easy, and the likelihood that you will be asked to
produce it in a first year calculus course is almost nil. So it is
given here as optional material for the curious and the brave.
This proof is not so hard that
a first year student can't understand it. So if you feel up to a challenge,
The intermediate value theorem has a partner that also seems obvious
called The extreme value theorem.
It is stated without
proof in almost every first year calculus text. This theorem says if
f(x) is continous on the closed interval,
All this is saying is that if you fasten one end of a clothes line to one pole and the other to another pole, it doesn't make any difference how much slack you leave or how many branches you drape it through, there will be a highest point on the clothes line and a lowest point on the clothes line. This is true because 1) the clothes line is continuous and 2) because the clothes line includes its endpoints.
In other words, a function that is continuous on a closed interval cannot run off to infinity or to minus infinity on that interval. It must remain always between some minimum value and some maximum value. Not only that, there must be a point, c, on the interval such that f(c) is the maximum value, and another point, d, on the interval such that f(d) is the minimum.
It is important that the interval be closed -- that is that it include the endpoints. If the interval does not include the endpoints, it is easy to come up with a counterexample. The function
x
f(x) = eq. 3.0-11
x2 - 1
is continuous on the open interval (that is excluding the endpoints) that
runs 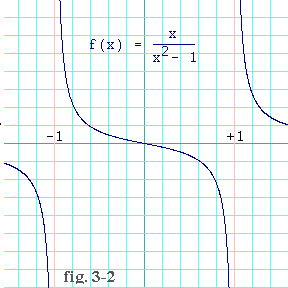
The proof of this theorem is even harder than that of the intermediate
value theorem, and you won't be asked to produce it in a first year
course. But it will be assumed that you know what the theorem means.
It plays a big role in the theory of maximums and minimums. For the
really brave, and because I hate to give you something as important
as this without proof, you can see the proof as optional material
by
The problems that follow are proofs. You should know that proofs concerning continuity may be on the exam.
Now here is one that you should be able to prove, and that you might
encounter on an exam. Suppose f(x) is continuous on the
closed interval
As always, make a sincere effort to work this problem on your own. If
you give up or if you want to compare your proof with mine,
Here's another theorem (which I call The Stepping Stone Theorem)
that you ought to be able to work through at least part of.
Prove that a function, f(x), is continuous at a point,
Notice that this is an "if or only if" proof. That means it is really two theorems in one. One theorem says that if for every set of stepping stones that leads to the river bank, the moss on the stepping stones leads to the moss on the riverbank, then the moss function is continuous at the riverbank. The other theorem is that if the moss is continuous at the riverbank, then for every set of stepping stones leading to the riverbank, the moss on them leads to the moss on the riverbank.
The usual approach to an "if and only if" theorem is to divide it into its two constituent theorems and prove each one separately. And that is what I recommend you do here. The second part of this one (that is the "only if" part) is the easier one to prove, so perhaps you should start with that. This part asserts that if the moss function is continuous at the riverbank, then each set of stepping stones that leads to the riverbank has moss that leads to the moss on the riverbank.
Approach it by demonstrating
that f(xn) can always be brought to within
e of f(c) (no matter how close to zero
you choose e) by making n big enough.
Remember that a sequence that has a limit will confine itself
to smaller and smaller intervals around its limit (in this case
the limit is c) as the subscripts get larger and larger.
You can bridge your logic to the delta-epsilon statement
of continuity by observing that the real numbers from
Go ahead and prove the "only if" part, and I'll give you a pass
on doing the more difficult "if" part. When you are done, you
can look at both proofs by
email me at hahn@netsrq.com