Section 3: Continuity continued

3.0 Track to the Future

(Combining Continuous Functions)

Suppose Marty McFly is riding a westbound train in the year 1885. We can label each point of the track with a real number that expresses how far from the station it is. To make it really useful, we would have to make sure we label all points to the east of the station with negative numbers and all points to the west of the station with positive numbers. The station itself would be at zero.

Likewise we could label all times with real numbers according to how many seconds had elapsed since noon of October 25, 1885. Times before that moment would be negative numbers, times after that moment would be positive numbers, and the moment itself would be time zero.

We have a sense that the position of the front of the train as a function of time is continuous. This is in line with our observation before that nature likes continuity. But what exactly do we mean by that?

In the previous section (3.0 Continuity: Places You Must Visit) we defined with precision what we mean by continuity of a real function of a real variable, and we did it using limits. In essence, we said that the train's position on the track as a function of time is continuous at a point in time, s, if the limit of its position, x_train(t), as time, t, goes toward s is, in fact, where the train ends up at exactly the moment s. To put that in our contract terms, you tell me how close the train has to be to the spot it will be at exactly s, and I can tell you how close in time you have to be to the time s to guarantee that the train will be that close.

We also said that if the above contract holds regardless of what time, s, you happen to choose, then the train's position as a function of time is continuous for all time. That's a pretty strong statement for a train, so let's just say that it's continuous from midnight, October 25, 1885 until midnight, October 26, 1885. In other words, it's continuous at least over the interval of that one day.

It seems that Marty brought his hover-board along on the train and is entertaining himself by scooting up and down the aisle on it. If we mark each point along the length of the train with a real number that indicates how far aft of the cowcatcher that point is (and to make this example work out right, we make all these numbers negative), then Marty's position on the train is a real function of time as well. Call it x_marty(t). And for the same reasons we believe the train's position on the track to be a continuous function of time, we believe that Marty's position on the train is a continous function of time as well (at least on the date in question).

                                 0 /
                                 |   Marty
                               / ^
                                / \     (shown: xmarty = -1.7)
            <   |         |         |         |
                0        -1        -2        -3
                         The Train      (shown: xtrain = 70.5)
           |         |         |         |         |         |         |
           71        70        69        68        67        66        65
       <   west              The Track                          > east

                              Fig 3-4

So what about Marty's position with respect to the tracks? Isn't that also a real function of time too? And how do we establish that function? We simply add the train's position to Marty's position on the train. In equation form, we have:

  xcombined(t)  =  xtrain(t) + xmarty(t)                         eq. 3.1-1

Actually, we can very easily. Remember that we have already proved (back in section 2.2) that the sum of the limits is the same as the limit of the sum. Since the new function is defined simply as the sum of two continuous functions, and since continuity is defined in terms of their limits, it follows immediately that the sum of two continuous functions is continuous. If the two functions are continuous in some places but not in others, then their sum is continuous everywhere where BOTH functions are simultaneously continuous (note that the sum might be continuous at a point where both summands are not, but it doesn't have to be. In other words, both summands being continuous is a sufficient condition for the sum to be continuous, but not a necessary condition). See if you can explain this same line of thought in the contract terms we have been using.

Since the product of the limits is the same as the limit of the products, it is also true that the product of two continuous functions is continuous. Again, if the two functions are continuous in some places but not in others, then their product is continuous everywhere BOTH functions are simultaneously continuous (again, both factors being continuous at a particular point is a sufficient condition for continuity of the product at that point, but not a necessary condition).

When it comes to the quotient of two functions, you have to be careful. Remember that the quotient function is not even defined wherever the denominator function is zero. So the rule is, the quotient of two continuous functions is continuous everywhere that the denominator is not equal to zero. Likewise, if the two functions are continuous in some places and not in others, then their quotient is continuous everywhere that they BOTH simultaneously continuous AND the denominator function is not zero (the analogous rule concerning sufficiency and necessity applies here as well, however, the quotient will never be continuous wherever the denominator is zero).

Let's go back to the train. A certain white-haired professor is also on the train. He set his watch to the station clock at exactly noon. But his watch does not work properly. Sometimes it speeds up and begins to run ahead of the station clock (which we shall assume is accurate), and sometimes his watch slows down until it runs behind the station clock. But the professor's watch always runs forward, never stops, and never jumps ahead instantaneously. In fact, the time his watch shows, which we shall call w(t), is a continuous function of the station clock time. In addition, if you knew the exact eccentricities of the watch, as the professor does, you could, at any time, deduce the time that the station clock reads by knowing the time on the professor's watch. And the function that takes us from the time on the professor's watch to the time on the station clock we shall call w^-1(t). And this function is continuous as well.

Remember the function x_train(t)? It is the position of the train based upon the station clock time. So what is the position of the train based upon the professor's watch time? If t_p is the time the professor's watch reads, then that would be:

  xpwatch(tp)  =  xtrain(w-1(tp))                                eq. 3.1-2

So what about the composite of two functions? For example, suppose f(x) = sqrt(x + 1) and g(x) = x². We already know that g(x) is continuous everywhere. I will tell you without yet giving you proof that f(x) is continuous whenever x >= -1. So, do you expect that f(g(x)) is also continuous? Intuition says it is, and in this case intuition is right. In fact, it is true that the composite of two continuous functions is also continuous. And if you you'd like to see the proof, click here.

But what about when the two functions are continuous in some places but not others? For example,

                         ______
  f(g(x))  =  f(x2)  =  Öx2 + 1                                eq. 3.1-3

And what about taking the opposite composite?

                 _____
  g(f(x))  =  g(Öx + 1)  =  x + 1                              eq. 3.1-4

So the rule about where a composite is continuous is more complicated than it was for sums, products, or quotients. It is this: the composite of two functions, f(g(x)), is continuous at every x at which g(x) is continuous AND f is continuous at g(x).

Coached Exercise: Show that Ö(x + 1) is Continuous

A little while ago I assured you, but without proof, that

             _____
   f(x)  =  Öx + 1

             _
   h(x)  =  Öx

             _____
   f(x)  =  Öx + 1

           _
   h(x) = Öx

First, we have g(x) = x + 1. Can you prove that it is continuous everywhere? If you were able to do the exercises in the last section, this will seem easy. Write the limit equation that expresses the continuity of this function. Now write it in contract form. If you do it right, your e expression will look exactly like your d expression. So the recipe for deriving d from e in this case is what? That is, what expression of e can you put in for d to make the contract always work? (hint: don't work too hard at it -- it's staring you in the face).

So now we know that g(x) is continuous everywhere. For now we are assuming that  h(x) = Öx is continuous wherever  x ³ 0. We know that

             _____      ____
   f(x)  =  Öx + 1  =  Ög(x)  =  h(g(x))                       eq. 3.1-5

And now the hard part that we've saved for last -- proving that  h(x) = Öx  is continuous wherever  x ³ 0. First write the limit equation for continuity of this function. Then write the contract.

In your e inequality, you ought to see the difference of two square roots. Looks pretty hard, eh? The trick in problems like this is to find the algebraic munging that you can do to it to make the hard thing look easier. You're going to use an error variable again. Let error be the difference of the two square roots. So your new e inequality should relate the absolute value of error to e.

Now take the equation you made that equates error to the difference of the two square roots and algebraically munge it so that there is only one square root on either side of the equal sign. Got that?

Now square both sides of that equation. Multiply out the square of the sum. Do you see that some of the terms are multiplied by of error (or its square) and some are not? Move all the ones that have error in them to one side of the equation, and move all the others to the other side.

Look at the side without the error terms. Does it look familiar? Will it look even more familiar if you take the absolute value of both sides? Doesn't that give you a recipe for d from error? And if you can get d from error, can you argue that you can also get it from e?

But note that your expression for d has a Öa in it. So your recipe for d only works where Öa is defined, and that is only where  a ³ 0. And so you have proved continuity for precisely the domain you set out to. Congratulations.

Step 1: Prove it for n = 1. That gets you onto the first rung of the ladder. When n = 1, then you have f(x) = x. You should be able to apply the delta-epsilon method yourself to a function as simple as this and prove that it is continuous. If you need to review it, read through the last section again. There are examples of such delta-epsilon proofs there.

Step 2: Prove that if you can get to the nth rung of the ladder, then you can get to the n+1st rung of the ladder. Once you have proved that and done step 1, it means that you can get to any rung of the ladder, right? So what do you have to do to show this? Going from the nth rung to the n+1st rung presupposes that you were able to get to the nth rung. So you presuppose that  f(x) = xⁿ  is continuous and demonstrate from it that  f(x) = xⁿ⁺¹  must also be continuous. But

   xn+1  =  (x)(xn)

So if  f(x) = xⁿ  is continuous, then it must also be true that  f(x) = xⁿ⁺¹  is continuous as well. So you can get to the first rung and from any rung you can get to the next. Hence,  f(x) = xⁿ  is continuous for every counting number, n.

Exercises

1) Let the function, f(x) be:

            1
   f(x)  =   
            x

2) Let the function, g(x) be:

            x2 - 1
   g(x)  =        
            x - 1

---

Optional Material: Strange Functions

I promised you earlier that I would show you examples of functions that were discontinuous in a variety of ways. We've seen that our friend, the unit step function, u(x), from the last section is continuous everywhere except at x = 0. Clearly the function u(x - j), where j is some integer is continuous everywhere except at x = j. If you add these up for all nonnegative integers, you get a staircase function:

                  ¥
 staircase(x) =   å  u(x - j)                                  eq. 3.1-6
                 j=0

For all negative x, staircase(x) is zero. For positive x, staircase(x) is 1 for  0 < x < 1,  2 for  1 < x < 2,  3 for  2 < x < 3, and in general it is n for  n-1 < x < n. It looks like a staircase with its bottom step at 0, and stepping up as you go right, as you can see in figure 3-5a. This function has a discontinuity at every nonnegative integer value of x. So here is a function with infinitely many discontinuities. Of course you could take the sum of only finitely many step functions and get a function that was discontinuous at only a finite number of places.

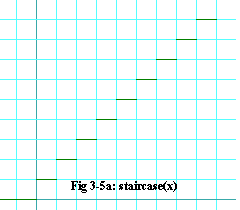
Now, let double_staircase(x) be as follows: double_staircase(x) = staircase(x) - staircase(-x) You can see double_staircase(x) in figure 3-5b. There is nothing especially remarkable about this function, but I am about to use it to make a most unusual function.

This new function, which you can call whatever you like, is made by arbitrarily setting it to zero at  x = 0. Everywhere else, though, we find its value by taking 1/x, sticking that into double_staircase, then taking one over that, or in other words, 1/double_staircase(1/x). Figure 3-5 shows a graph of this function. As you can see, the discontinuities bunch up as it gets close to zero. Unfortunately there are limits to the graphing capabilities of any display, and here the discontinuities drop below the accuracy of the graph as you move even moderately toward zero. But they are there in the actual function. In fact, there are infinitely many of them in any interval that contains  x = 0, no matter how small that interval is. But, surprisingly, this function is continuous at  x = 0. Can you prove that?

How about a function that is discontinuous everywhere. Suppose you had a function that assigned a value of 1 to any real number that can be represented by a terminating decimal, and assigned 0 to any real number that cannot. So at  x = 0.1, for example, this function would be 1, and at  x = 1/3 it would be 0. This function is discontinuous everywhere. That is because as close as you like to any value that can be expressed as a terminating decimal, there is one that cannot, and vice versa. Think about it. Try the limit test for continuity at any point.

I promised you also a function that is continuous at a single point only. Try this. Take the function given above that is discontinuous everywhere and multiply it by x². The resulting function is continuous only at  x = 0. See if you can prove that as well.

Finally, here is a continuous function that cannot be graphed. You will have to recall your understanding of the sin function for this. This function is described as an infinite sum of sin terms. The way we define infinite sums is this. The sum of an infinite number of terms is the limit (if it exists) of the partial sums of the first n terms, as n goes to ¥. Here is the formula:

             ¥
             å   2-n sin(3nx)                                    eq. 3.1-7
            n=1

The sin(x) function, you probably remember, is that ripply thing that goes on smoothly and evenly forever. Well this takes a ripple and adds a smaller yet faster ripple to that, then adds a still smaller and still faster ripple to that, and so on. I shall state without proof at this time that the function in 3.1-7 is defined everywhere and is continuous everywhere. But it has a fractal nature to it, and hence cannot be graphed. Fractals have been much in the news this past decade, but this function, and a weird property it has (which I will discuss in a later section) have been known for over a century.

---

Return to table of contents

Move on to Derivatives

email me at hahn@netsrq.com