

The lion, as we all know, is king of the beasts. The other animals live in fear of him and his appetite for their flesh. And so it came to pass that Giraffe, Zebra, Gazelle, and Warthog decided to make a public works project of protecting themselves from the lion.
"We all know that the lion is lazy," said Zebra. "Perhaps while he naps the afternoon away, we might trap him inside his lair."
"By what means?" asked Gazelle.
"We shall pile up dirt around his lair to make a wall," suggested Warthog.
Giraffe was silent, because, as everybody knows, Giraffe has no voice.
And so the project was agreed to. On the designated afternoon, hundreds of animals came to help move earth to erect the wall. As the sun sunk low, the wall was complete.
"But how shall we know if the sides of the wall are steep enough?" asked the zebra.
"One of us will have to test them," said Warthog.
And so they sent Giraffe. Giraffe ran toward the wall. When he reached its base, he bounded to the top in just one stride. There he observed that his height was exactly half the horizontal distance he had bounded. He returned to the others and wrote, "50% grade," in the sand.
This upset Zebra. "Does anybody doubt that the lion is sure-footed enough to negotiate a 50% grade?" he asked. "I was certain we had built the wall steeper than that. I myself shall go and inspect it."
And off he ran. Like Giraffe, when Zebra reached the base of the wall, he bounded up. But Zebra, whose legs are shorter than Giraffe's, needed two strides to reach the top. Once there, he observed how high he was and where his footprint was in the middle of the wall. He hurried back to the others and reported, "My observation is that the wall begins with a 75% grade, then shallows out to a 25% grade halfway up."
This time it was Gazelle who was miffed. "We worked so hard at that wall," he complained, "yet I would have no trouble scrambling up a 75% grade. The lion wouldn't either. I too shall inspect the wall."
And off he ran. He too reached the base of the wall and bounded up from there. But Gazelle's legs are even shorter than Zebra's, and he needed four strides to reach the top. He too observed the height of his footprints, then hurried back to give his report. "It's not as bad as Zebra makes it out to be," he said. "It seems that the wall begins with an 87.5% grade, then a quarter of the way up goes to a 62.5% grade, then halfway up to a 37.5% grade, and from three quarters up to the top, it's a 12.5% grade."
Warthog wasn't sure whether the lion could climb such a wall or not. But he was sure he was the only one of the four who had not yet spoken on the subject. And being one who liked the sound of his own voice, "I'll check it too," he said, and off he went.
 |
 |
It took the short-legged Warthog eight strides to reach the top. And he took the time to figure the grade from each of his footprints. The first eighth of the way was a 93.75% grade, the second eighth an 81.25% grade, the third eighth a 68.75% grade, the fourth eighth a 56.25% grade, the fifth eighth a 43.75% grade, the sixth eighth 31.25% grade, the seventh eighth an 18.75% grade, and the last eighth a 6.25% grade.
And while he pondered all this, he heard a yawn from inside the wall. "You foolish creatures," came a sleepy voice. It was, of course, the lion. "You think you have penned me in, yet each of you is able to climb the wall to measure it. And do you think I would be unable to climb it just to fetch something as mundane as my dinner? Tonight I'll be having ham and bacon, and I'm certain you'll be joining me."
Figure 4-1 shows a graph of the profiles that each of the animals
perceived climbing the wall.
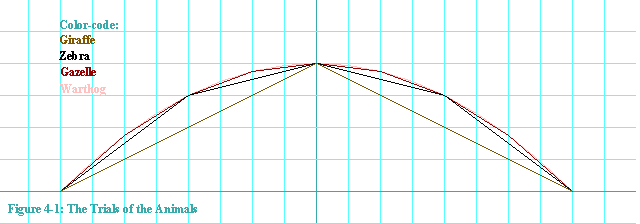 Because Giraffe could bound 8 meters horizontally in each stride, he saw the
entire wall to have the same slope. Zebra saw it differently because
he could only go 4 meters per stride. Gazelle could only go 2, and
Warthog only 1. And so each saw his own version of the wall.
Because Giraffe could bound 8 meters horizontally in each stride, he saw the
entire wall to have the same slope. Zebra saw it differently because
he could only go 4 meters per stride. Gazelle could only go 2, and
Warthog only 1. And so each saw his own version of the wall.
But look at what they each saw in their first bound. Giraffe: 50% grade, Zebra: 75% grade, Gazelle: 87.5% grade, and Warthog 93.75% grade. And by grade, I mean the percentage that the wall goes up of each unit it goes horizontally. After Warthog's demise, Rabbit, satisfied that the lion was no longer hungry, tried the first step of the wall. Rabbit went 0.5 meters horizontally and found the initial grade to be 96.875%. Mouse went 5 cm horizontally up the wall and found the initial grade to be 99.6875%. Ant tried it, going 1 mm horizontally in his first step, and found the grade to be 99.99375%.
With a little experimentation, you will see that all the numbers given above are consistent with the following function:
-x2
f(x) = + 4 eq. 4.0-1
16
f(x) represents the height of the wall as a function of how
far you are from its center, which is given at
And how did each animal figure out the percent grade that he perceived? He
simply took the vertical progress of one step and divided by the horizontal
progress of that same step. For example, Giraffe took a huge bound 4 meters
vertically and 8 meters horizontally. So he divided it out and saw a 50%
grade on his first (and only) step. Ant, on the other hand, took a tiny
step of 0.999375 mm vertically and 1.000000 mm horizontally. When he divides,
he gets a 99.9375% grade.
We see that at the base of the wall, the size of your stride makes a big
difference as to the grade you will experience. But as the strides get
tinier and tinier, the grade that the tiny animals experience seems to
approach a limit of 100%. So, is it true for this wall that at
vertical progress
lim = 100% eq. 4.0-2
step size > 0 horizontal progress
What each animal perceived was an average grade over his step
size. At the base of the wall, that average started at the base
(ie
So, what is horizontal progress? Well, that's simply step size. For
reasons that are tied up in tradition, I will call the step size, h.
What about the vertical progress. Well, each animal starts at the base
of the wall, takes a step, and goes up a little. If the animal starts
out at -8 and has a horizontal step size of
vertical progress = f(-8 + 0.1) - f(-8) = eq. 4.0-3
æ -(-7.9)2 ö æ -(-8)2 ö
ç + 4 ÷ - ç + 4 ÷ = 0.099375
è 16 ø è 16 ø
Or, if we simply wanted to stick in the step size symbol, h, we
would have:
vertical progress = f(-8 + h) - f(-8) = eq. 4.0-4
æ -(-8 + h)2 ö æ -(-8)2 ö
ç + 4 ÷ - ç + 4 ÷
è 16 ø è 16 ø
If you multiply out the square, then you have:
vertical progress = f(-8 + h) - f(-8) = eq. 4.0-5
æ -64 + 16h - h2 ö æ -64 ö
ç + 4 ÷ - ç + 4 ÷
è 16 ø è 16 ø
A lot of stuff cancels in 4.0-5. The -64's go away and the
4's go away as well. That leaves you with:
16h - h2
vertical progress = f(-8 + h) - f(-8) = eq. 4.0-6
16
And now we're supposed to divide that by the horizontal progress to get
the grade. But the horizontal progress is simply the step size, h.
So now we have:
vertical progress f(-8 + h) - f(-8) 16h - h2
= = eq. 4.0-7
horizontal progress h 16h
Finally, we wanted to know if there was a limit to the grade as the step
size, h, goes to zero. Look at the right-hand part of 4.0-7. Didn't
we demonstrate a rule back in
section 2.5 for finding the limit of the
quotient of two polynomials as x goes to zero? Isn't that
exactly what we have here, except with h taking the place of
x?
(Note also that the polynomial in the numerator is written backwards
from the tradition way -- that is it has it's highest power last, and the
traditional way to note it is with the highest power first. But it makes
no difference what order we sum a thing in, right?)
Recall that the rule from section 2.5 was simply to find
the coefficients
of the lowest power in the numerator and denominator that are not both
zero. We proved that rule, so here we can just apply it and not
bother with all that delta-epsilon stuff.
The coefficients that the rule specifies in this case are 16 for
the numerator and 16
for the denominator (that is, the 1st power coefficients).
The rule says to simply take their ratio, which
is 1, or in percent, that's 100%. And that is what the exact
grade at exactly the base of the wall must be.
But what if we have a more general interest in the grade of the wall? What if just knowing its grade at the base is not enough? We would like to know the grade of the wall as a function of how far, horizontally, we are from the wall's center.
Let's do the same thing we just did, but instead of putting in -8 (which corresponds to the base of the wall), let's just put in x, which corresponds to any point on the wall you'd like. If you take a 0.1 meter step horizontally anywhere on the wall, your vertical progress is:
vertical progress = f(x + 0.1) - f(x) = eq. 4.0-8
æ -(x + 0.1)2 ö æ -x2 ö
ç + 4 ÷ - ç + 4 ÷
è 16 ø è 16 ø
If you multiply out 4.0-8 and do cancellations (which I'm sure you are
busy doing in your notebook as you read along), you will get:
-(2x × 0.1 + 0.12)
vertical progress = f(x + 0.1) - f(x) = eq. 4.0-9
16
You can see that the size of the vertical step we take is not just dependent
upon the size of the horizontal step, but also dependent upon where you are
on the wall (that is at what x) you are when you take that step. The
more negative x is, the more the vertical progress will be with
each 0.1 meter horizontal step you take. If x is positive,
which means that you are past the center of the wall, then your vertical
progress is definitely negative, that is you are going down hill, toward the
lion's lair.
But what if we take steps even smaller than 0.1 meters? What if we want to know the limit of the grade as the step size goes toward zero? Let's do the 4.0-8 and 4.0-9 again, except this time let's put in the variable step size, h, instead of the fixed size, 0.1.
vertical progress = f(x + h) - f(x) = eq. 4.0-10
æ -(x + h)2 ö æ -x2 ö
ç + 4 ÷ - ç + 4 ÷
è 16 ø è 16 ø
Go ahead and multiply out the square then cancel whatever cancels. You
should get:
-(2xh + h2)
vertical progress = f(x + h) - f(x) = eq. 4.0-11
16
But vertical progress is not what we are really interested in. What we want to know is what is the grade? Remember that grade is vertical progress divided by horizontal progress. And remember that the horizontal progress is simply the step size, h. So to get the grade you divide 4.0-11 by h.
vertical progress f(x + h) - f(x) -(2xh + h2)
= = eq. 4.0-12
horizontal progress h 16h
But this still gives us the average grade over a step of horizontal
length, h, starting at the point x. We don't want the
average. We want the exact grade at exactly x. And
to find that, we take the limit as the step size, h, goes toward zero.
Once again, 4.0-12 shows that we have the quotient of polynomials. Don't
be confused. The variable, h, is playing the role that x
played back in
section 2.5. So to apply the rule we
established back in section 2.5, we have to find the lowest power of h
at which the numerator coefficient and the denominator coeffecient are not
both zero. Again that occurs in the 1st power of h.
The numerator coefficient of the 1st power of h is simply whatever we multiply by the term, h, in the numerator. In this case, it's 2x. The denominator coefficient whatever we multiply by the term, h, in the denominator. In this case, it's 16. The rule tells us to use the quotient of those two for the limit. So the grade is:
f(x + h) - f(x) 2x
grade(x) = lim = eq. 4.0-13
h > 0 h 16
Now, if I give you any horizontal point on the wall, x, you can give me the grade at that point by multiplying x by 2/16 (if you want the grade in percent, you must, of course, multiply that result by 100%). The point is, the grade is a function of x, just as the height of the wall, f(x), is. If you name an x, I can tell you both the height of the wall, f(x), and the grade of the wall, grade(x). Notice that we derived the function grade(x) from f(x), and hence, we call grade(x) the derivative of f(x).
Another everyday example of the derivative of something is speed. Suppose you drive from home to your friend's house 60 miles away. It takes you 1 hour. Clearly your average speed is 60 miles per hour. But was that your speed the whole way? You might have stopped at McD's and ate a burger and fries for half an hour, then whipped along at 120 miles per hour the rest of the time.
But let's say that you don't like to get speeding tickets, and you drove around 60 miles per hour the whole way. If there are mile markers along the road every tenth of a mile, you can gauge your speed by measuring the time elapsed between passage of mile markers, and dividing that elapsed time (converted to hours) into 0.1 miles. Still, that only gives you the average speed over that period of time. Within a 0.1 mile distance you may have slowed to 50 mph to avoid rear-ending a school bus, then accelerated to 70 mph in order to pass it. But your reckoning of speed by the mile markers still indicates 60 mph.
Your speedometer ought to give you a better reckoning of your instantaneous speed. Modern speedometers work by counting the number of magnetic ticks on an automobile's drive shaft that pass by a sensor in some fixed period of time. Let's say that time is 0.1 seconds. The computer in the dashboard knows how much travel distance each tick represents. It can multiply each count by that distance (in miles), then divide by 0.00002778 hours (which is the same as 0.1 seconds), and lo, it has computed your average speed in miles per hour over a tenth of a second.
But that is still not your instantaneous speed. If you had an old-style speedometer, it might work by spinning a centrifugal lever at the same rate as the drive shaft. The lever would be attached to a spring. The degree to which the lever stretched the spring would be an instantaneous measure of your speed. In this case, by using a mechanical trick, we avoided having to take a limit. But the centrifugal mechanism does, in it's own way, determine the limit of distance traveled divided by elapsed time as elaped time goes toward zero. And that is, in fact, the definition of instantaneous speed.
At any time, t, during your trip, there is a number, x, which represents how far you have traveled up to that moment. So we have a function of time, x(t), that represents your distance traveled. At any moment, t, we also have your instantaneous speed, v(t), assuming you have a suitable way of measuring it. It is true that:
x(t + h) - x(t)
v(t) = lim eq. 4.0-14
h > 0 h
What 4.0-14 means is, "find the distance between where you are now and where you'll be in a short time, h, from now. Divide that by the time that elapses until then, which is also h. Your instantaneous speed, right now, is the limit of that quotient as the elapsed time, h, goes toward zero." And so, the instantaneous speed is derived from what your position is at various times. That is why speed (or more properly, velocity) is the time derivative of position, or more commonly, the derivative of position with respect to time.
Move on to section 4.1: The Main Pillar of the Temple
email me at hahn@netsrq.com