Section 4: DerivativesKCT logo

© 1996 by Karl Hahn

4.2 Rules to Live By

So far we have covered how to take the derivative of a very narrow class of functions, that is the class of functions in the form of  g(x) = xn.  We also know that the derivative of  f(x) = mx + b  is equal to m for all x. But what a pain life will be if we have to go through the business of 

                    f(x + h) - f(x)
   f'(x)  =   lim                                                eq. 4.2-1
             h  > 0       h
every time we want to find the derivative of a new function. For example, if I wanted to know the derivative of  f(x) = 3x3 - 6x2 + 4x - 3,  which is simply a combination of functions whose derivatives we already know, do I have to apply 4.2-1, apply all the hairy algebra, and then take the limit?

No.

Mathematics is all about finding (and proving) rules, then applying them to make your life easier. We will demonstrate and prove several very simple rules here for finding the derivative of a functions that are concocted of sums, products, or composites of functions whose derivatives we know. These rules are powerful and meant to last a lifetime, so remember them well. In the rest of your calculus career, you will have to apply them often.

The Derivative of a Sum

Let's return to the animals, who are frustrated at the uselessness of the wall that they all labored so hard at. They meet again, but feel resigned to becoming dinner whenever the lion grows hungry.

"If Warthog were still with us," said Zebra, "he would think of something."

"The problem is clear," said Gazelle. "If the wall is not too steep for us to climb, then the lion can certainly climb it as well. So the logical solution is to amend our wall so that it is too steep for any of us to climb."

Giraffe began pawing at the ground and waving his head around, which is his way of saying, "So what's your proposal?"

"What we shall do," said Gazelle, "is pile up more dirt. We don't need any more at the base of the wall, but as we go in from the base, we shall add more and more dirt. That is what will make it steeper. At one meter in, I propose that we will adding an additional half meter of dirt. At two meters in, we shall be adding a full additional meter. And so on, adding dirt at a rate such that each meter in from the base adds an additional half meter of dirt. That should increase the grade at the base to a whopping 150%. And that's steeper than I can climb."

And so the animals proceded with this plan. It required the best engineering skills the animals could bring to the effort. You see, they had to figure out ways to get dirt to the top of a wall that was too steep for any of them to climb. But alas, they steepened only the outside of the wall, which prevented any of them from getting into the lion's lair. But it did not prevent the lion from getting out.

But whether they ever keep the lion at bay or not is beside the point. My question to you is, was Gazelle's assumption that the grade at the base would increase to 150% a valid one? We already determined that the grade at the base of the original wall is 100%. If the animals piled up dirt on flat ground in the manner that Gazelle has proposed, they would end up with a ramp that had a constant grade of 50%. Gazelle figured that if you place one pile of dirt on top of the other, the grades will simply add. Seems reasonable, but can we prove it?

Gazelle's logic certainly works with straight line functions. Suppose we have  f1(x) = m1x + b1  and  f2(x) = m2x + b2.  We already know that their derivatives are m1 and m2 respectively, regardless of x. When we add them together, we get: 

   f1(x) + f2(x)  =  (m1 + m2)x + b1 + b2                        eq. 4.2-2
This is the equation of straight line with a slope of  m1 + m2.  Since we know that the derivative of a straight line is the same as its slope, the derivative of this line is also  m1 + m2.  That is precisely the sum of the derivatives of the two summand functions. But is it always true that the derivative of the sum is the sum of the derivatives?

Let's explore in more detail what is going on in 4.2-1. Every time we've used it, we've had to deal with the expression,  f(x + h).  When we did the derivative of  f(x) = mx + b,  some good, old fashioned linear algebra got us an expansion of  f(x + h).  When we did the derivative of  g(x) = xn,  we used the binomial theorem to get us an expansion of  g(x + h).  In both cases the expansion consisted of either  f(x)  or  g(x)  plus a bunch of other stuff. The  f(x)  or  g(x)  cancelled, and we were left to take the limit of the other stuff.

So I am going to give the other stuff a name. I am going to say that  f(x + h)  always expands to: 

   f(x + h)  =  f(x) + Df(x, h)                                  eq. 4.2-3
Clearly Df (that's Greek letter, delta) can vary with both x and h, and that is why x and h are both shown inside the last parentheses. It is because Df is a function of both of them.

Let's now substitute 4.2-3 into 4.2-1: 

                    f(x) + Df(x, h) - f(x)
   f'(x)  =   lim                                                eq. 4.2-3
             h  > 0           h
When we take the cancellation, we are left with: 
                    Df(x, h)
   f'(x)  =   lim                                                eq. 4.2-4
             h  > 0    h
This limit can only exist if  Df(x, h)  goes toward zero as h does. See if you can explain why.

But more importantly, if 4.2-4 is to hold, then as h gets closer and closer to zero,  Df(x, h)  must start looking more and more like  h f'(x).  Whatever content  Df(x, h)  has in addition to  h f'(x)  must shrink away to insignificance when compared with  h f'(x).  Why? Because if it didn't, the limit would not go to  f'(x). 

But that means that: 

         Df(x, h)            h f'(x)
   lim             =   lim                                       eq. 4.2-5
  h  > 0     h        h  > 0    h
whenever f'(x) exists. But recall that  Df(h, x)  is nothing more than what's left after we take  f(x)  from  f(x + h).  This is the observation that will allow us to derive all of our rules. It means that in the limit we are taking in 4.2-1, whenever we see  f(x + h),  we can substitute  f(x) + (h f'(x) ).  And we will be doing that often.

So how do we apply that to the sum of two functions? Suppose we have  u(x) = f(x) + g(x).  We already know what  f'(x)  and  g'(x)  are. So how do we figure out what  u'(x)  is?

Since  u(x)  is the sum of  f(x)  and  g(x),  let's substitute their sum into 4.2-1: 

                    f(x + h) + g(x + h) - f(x) - g(x)
   u'(x)  =   lim                                                eq. 4.2-6
             h  > 0                h
And now the substitution that we can make from what we observed in 4.2-5 (substituting  f(x) + (h f'(x) )  for  f(x + h),  because in the limit, they must be the same. Likewise for < nobr>g(x + h)):  
                    f(x) + (h f'(x) ) + g(x) + (h g'(x) ) - f(x) - g(x)
   u'(x)  =   lim                                                      
             h  > 0                        h

                                                                 eq. 4.2-7
Taking the cancellations we get: 
                    (h f'(x) ) + (h g'(x) )
   u'(x)  =   lim                                                eq. 4.2-8
             h  > 0           h
Factoring an h out of the numerator, we have: 
                    h (f'(x) + g'(x) )
   u'(x)  =   lim                                                eq. 4.2-9
             h  > 0         h
This is now in a form where we can apply the rule we developed in section 2.5. When we apply the rule and take the limit, we get that: 


   u'(x)  =  f'(x) + g'(x)                                       eq 4.2-10

Since  u(x)  was defined as being the sum of  f(x)  and  g(x),  we have proved here that the derivative of the sum is always equal to the sum of the derivatives, just as Gazelle had assumed. This works with any two functions you care to add, as long as both their derivatives exist.

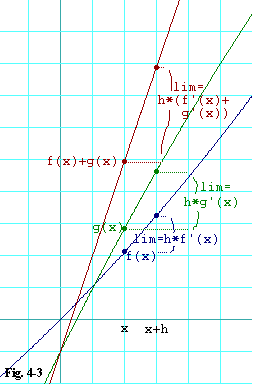
Figure 4-3 attempts to show graphically what is going on when you take the derivative of a sum. You can see that I have labeled two points on the x axis, x and  x + h  respectively. Dots are shown on each of the three traces  (f(x)  in blue,  g(x)  in green, and the sum in red) at those two points. You can imagine how, as  h  gets small, the vertical distance from  f(x)  to  f(x + h)  (in the case of the blue function) gets closer and closer to  h f'(x).  Likewise with the green function,  g(x).  In the red trace, the vertical spread of the sum must be the sum of the vertical spreads of the red and green traces. You get the approximation of the derivative of each trace by dividing the vertical spread by the horizontal spread, h. And in the limit, these approximation become as accurate as you like. Hence, the derviative of the sum must be the sum of the derivatives.

Figure 4-3

Exercises

1) Use the sum rule and what we know about the derivatives of  f(x) = mx + b  and  g(x) = xn  to find the derivatives of: 

f(x) = x4 + x3

f(x) = x2 - 7x  + 12

2) A constant function is one that sets  f(x)  to some constant regardless of the value of x. For example  f(x) = 3  is a constant function. Notice that a constant function is simply an  f(x) = mx + b,  but with m set to zero. Use that fact to argue that the derivative of a constant function is always zero.

3) If  f(x)  is some function whose derivative exists and n is a counting number, then let  g(x) = n f(x).  Can you argue using the sum rule that  g'(x) = n f'(x)?  Can you further argue that if  u(x) = f(x) / n,  then  u'(x) = f'(x) / n? 

View Answers

Derivative of a Product

With the invention of programmable inks, a clever entrepeneur who runs a tattoo parlor in Singapore now features animated tattoos. You pick any one of several hundred one to three second videos, pay the man an exorbitant sum, strap yourself into his computerized tattoo-stylus, and a few hours later you walk out with that very video playing over and over again on your chosen patch of skin (this is all BS, but bear with me).

One of the very first customers for this treatment was a merchant marine diesel-engine jockey named Motorhead McCay. It seems that Motorhead had his entire large chest done with a slow-mo video of Michael Jordan leaping from right around Motorhead's navel and slam-dunking a basketball through a hoop somewhere near Motorhead's collar bone.

If Motorhead holds his breath, lungs empty, you can plot Michael Jordan's height above Motorhead's navel as a function of time. From beginning (at  t = 0)  to end (at  t = 2)  of the two second video, this function,  hempty(t)  (which stands for height in centimeters, lungs-empty), is: 

   hempty(t)  =  10(2t - t2)                                      eq. 4.2-11

Of course Motorhead cannot hold his breath for very long. When he breathes in the size of his chest increases by 10%. So with a full gulp of air, the function is a bit different: 

   hfull(t)  =  11(2t - t2)                                       eq. 4.2-12

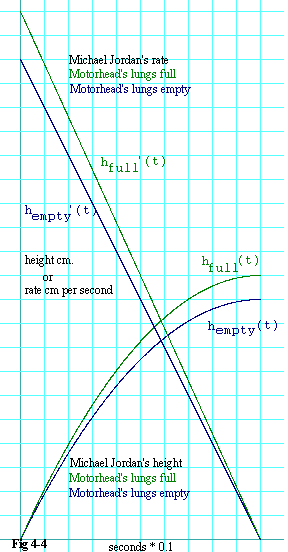
Figure 4-4 shows Michael Jordan's height above Motorhead's navel as a function of time with lungs full (green) and lungs empty (blue). It also shows his ascent rate in both cases, which is the time derivative of his height.

Now let's say that we can freeze-frame the tattoo video at the moment that Michael Jordan is 10 cm above Motorhead's navel. With the video frozen, we tell Motorhead to breath normally. He breathes in, and Michael Jordan goes to 11 cm. He breathes out again, and Michael Jordan goes back to 10 cm. Let's say that it takes one second for Motorhead to inhale all the way from lungs empty to lungs full. And let's say that his chest expands at a constant rate when he does so.

The rate of Michael Jordan's ascent is the time derivative of his position on Motorhead's chest. We have seen that Michael Jordan appears to move if Motorhead holds his breath and the video runs, and if Motorhead breathes while the video is frozen.

If Motorhead breathes while the video runs, it gets even more interesting. Suppose he begins to inhale at the moment the video begins. The size of his chest as a fraction of its lungs-empty size is:

Figure 4-4 

   c(t)  =  1 + 0.1t                                             eq. 4.2-13
and Michael Jordan's height above Motorhead's navel (for the first second) becomes: 
   c(t) hempty(t)  =  (1 + 0.1t) (10) (2t - t2)                   eq. 4.2-14
So what is Michael Jordan's ascent rate during that second? Well let's see what it is if he holds his breath first. If he holds his breath with lungs empty, then: 
   hempty'(t)  =  (10) (2 - 2t)  =  c(0) (10) (2 - 2t)            eq. 4.2-15
Note that by 4.1-13,  c(0) = 1.  Note also that we have applied what we learned in exercise 3 above. If Motorhead holds his breath with lungs full, we get (again recalling exercise 3): 
   hfull'(t)  =  (11) (2 - 2t)  =  c(1) (10) (2 - 2t)             eq. 4.1-16
which is the same as c(1) hempty'(t). And it seems intuitive that if Motorhead holds his breath at any degree of fullness in between (ie,  1 < c < 1.1)  we ought to be able to find Michael Jordan's ascent rate by multiplying  hempty'(t)  by whatever fraction Motorhead's chest is expanded. So, for example, when his chest is halfway expanded, you would have an ascent rate of  1.05 × hempty'(t). 

Let's look again at the other case, where we freeze the video, but Motorhead gets to breathe. If we freeze it at the beginning, before Michael Jordan begins his leap, then as Motorhead inhales, Michael Jordan doesn't ascend at all. He's stuck at Motorhead's navel. So his ascent rate is zero. But if we freeze the video when Michael Jordan is at the top of his leap, then as Motorhead inhales, Michael Jordan goes from 10 cm. high to 11 cm. high in one second, for an ascent rate of 1 cm. per second. And if we freeze the video when Michael Jordan is only halfway up (that is 5 cm. high) and Motorhead inhales, then Michael Jordan goes from 5 cm. to 5.5 cm. for an ascent rate of 0.5 cm. per second.

We can find the time derivative of Motorhead's breathing (that is of  c(t))  using material we have already covered (hint: this is an  mx + b  problem). 

   c'(t)  =  0.1                                                eq. 4.2-17
(but only while Motorhead is inhaling). Notice that freeze-frame ascent rate is simply  c'(t)  times what Michael Jordan's height was frozen at when Motorhead's lungs were deflated.

So at one extreme we hold Motorhead's chest constant and run the video and we get an ascent rate equal to Motorhead's degree of lung inflation times  hempty'(t).  At the other extreme, we hold the video constant and let Motorhead breathe and get an ascent rate of Michael Jordan's frozen height (with Motorhead's lungs empty) times  c'(t). 

If we let Motorhead breathe and run the video at the same time, would it surprise you if the ascent rate were simply the sum of these two? That is, if the Michael Jordan's height,  u(t),  were given by: 

   u(t)  =  c(t) hempty(t)                                       eq. 4.2-18
then would it surprise you if his rate,  u'(t),  were given by: 
   u'(t)  =  (c(t) hempty'(t) ) + (c'(t) hempty(t) )              eq. 4.2-19
This sum -- that is one factor times the derivative of the other plus the other factor times the derivative of the first -- is how we find the derivative of any product.

The rule for taking the derivative of a product is:

If 

   u(x) = f(x) g(x)                                              eq. 4.2-20a
then 
   u'(x) = (f'(x) g(x) ) + (f(x) g'(x) )                         eq. 4.2-20b

In the example given, we know that  hempty'(t) = 10(2 - 2t)  and that  c'(t) = 0.1.  So if  u(t) = hempty(t) c(t),  then, substituting into 4.2-19, we find Michael Jordan's ascent rate, u'(t), with the video running and Motorhead breathing is: 

   u'(t)  =  ( (1 + 0.1t) (10) (2 - 2t) ) + ( (0.1 × 10) (2t - t2) )

                                                                  eq. 4.2-21
Please do the substitutions yourself on a sheet of paper. You can get  hempty(t)  from 4.2-11,  hempty'(t)  from 4.2-15,  c(t)  from 4.2-13, and  c'(t)  from 4.2-17. Make sure you understand how we arrive at 4.2-21.

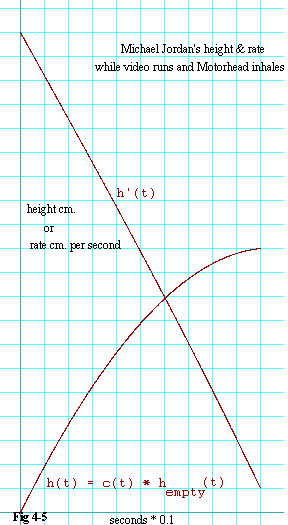
Figure 4-5 shows Michael Jordan's height,  u(t),  and rate,  u'(t),  as functions of time if the video runs and Motorhead is allowed to inhale with his chest expanding according to the function,  c(t).  Compare this graph carefully with the ones shown in figure 4-4. Notice that  u'(t)  does not end up at zero at  t = 1.0 second  the way both rate functions do in figure 4-4. This is because Michael Jordan's ascent does not stop at t = 1.0 second. Even though the video has Michael Jordan at the top of his leap, Motorhead's chest is still expanding, and so Michael Jordan must still be ascending at that moment. Notice also that the rate function,  u'(t)  is not a perfectly straight line as the rates were in figure 4-4. And this agrees with equation 4.2-21, which is not the equation of a straight line.

To prove the product rule, we can use the same technique as we did proving the sum rule. That is, we substitute the product into 4.2-1, then replace  f(x + h)  with  f(x) + (h f'(x) )  and replace  g(x + h)  with  g(x) + (h g'(x) ). 

Figure 4-5 

                    (f(x + h) g(x + h) ) - (f(x) g(x) )
   u'(x)  =   lim                                                eq. 4.2-22
             h  > 0                h
which we get by substituting the product of  f(x)  and  g(x)  into 4.2-1. When we make the further substitutions we get: 
                    ( (f(x) + hf'(x) ) (g(x) + hg'(x) ) - (f(x) g(x) )
   u'(x)  =   lim                                                     
             h  > 0                        h

                                                                 eq. 4.2-23
I know this is starting to look messy, but it won't be so bad if you read it in your own handwriting. When you multiply this out and take the cancellation of the  f(x)g(x)  terms, you end up with: 
                    (f(x)  hg'(x) ) + (g(x) hf'(x) ) + (h2f'(x)g'(x) )
   u'(x)  =   lim                                                     
             h  > 0                        h

                                                                 eq. 4.2-24
or, factoring out the h from the first two summands: 
                    u(f(x)g'(x) + f'(x)g(x) ) + h2f'(x)g'(x)
   u'(x)  =   lim                                           
             h  > 0                    h

                                                                 eq. 4.2-25
Now you have a polynomial in h in the numerator and a polynomial in h in the denominator. You can use the rule we developed in section 2.5 to take the limit. The lowest power of h we see here is h1. So the  h2  term drops out of the limit. And the ratio of the coefficients of h leaves us with the product rule (which is already shown in 4.2-20b).

Alternative Proof to the Product Rule

Your instructor might have used an approach more similar to what follows than to what I just gave above. Look at the following proof, and if it seems more familiar to you than the above, then it is the one you should reproduce on an exam if asked.

We begin the same way as before -- by writing out the limit formula for the derivative: 

                    (f(x + h) g(x + h) ) - (f(x)g(x) )
   u'(x)  =   lim                                           eq. 4.2-26
             h  > 0                h
Now, you can always add zero to anything and that anything is left unchanged. and we know that anything minus itself is always zero. So clearly  -f(x)g(x + h) + f(x)g(x + h) = 0.  Let's add that to the numerator of equation 4.2-26. So here is just the numerator of 4.2-26 with the above expression added to the middle of it: 
   (f(x + h)g(x + h) ) - f(x)g(x + h) + f(x)g(x + h) - (f(x)g(x) )

                                                                  eq. 4.2-27
By factoring, we can see that this is the same as 
   (f(x + h) - f(x) )g(x + h) + f(x)(g(x + h) - g(x) )          eq. 4.2-27
Putting that back in for the numerator of equation 4.2-26 we have 
                    (f(x + h) - f(x) )g(x + h) + f(x)(g(x + h) - g(x) )
   u'(x)  =   lim                                                      
             h  > 0                          h

                                                                  eq. 4.2-28
which is the same as 
                    (f(x + h) - f(x) )g(x + h)  f(x)(g(x + h) - g(x) )
   u'(x)  =   lim                             +                       
             h  > 0             h                          h

                                                                  eq. 4.2-29
But the left-hand summand is simply the limit formula for  f'(x)  times  g(x + h)  and the right-hand summand is simply the limit formula for  g'(x)  times  f(x).  With that in mind, we see that equation 4.2-29 is the same as 

   u'(x)  =   lim   f'(x)g(x + h)  +  f(x)g'(x)                   eq. 4.2-30
             h  > 0
And as h goes to zero,  g(x + h)  goes to  g(x),  so we have, in the end 
   u'(x)  =  f'(x)g(x)  +  f(x)g'(x)                              eq. 4.2-31
which is what we were trying to prove.

Some Worked Examples

Example 1: Find the derivative of: 

   u(x)  =  (mx + b) (x2 - 3x + 2)
This thing is clearly a product. If we say that  f(x) = mx + b  and  g(x) = x2 - 3x + 2,  we can find the derivatives of  f(x)  and  g(x)  using techniques we already know. We know that  f'(x) = m.  We can apply the sum rule to  g(x)  to find that  g'(x) = 2x - 3. 

We now apply the product rule (equation 4.2-20b), but substituting the expressions we have in the problem for  f(x),   g(x),  and their derivatives. 

   u'(x)  =  (m (x2 - 3x + 2) ) + ( (mx + b) (2x - 3) )
which is the answer. You can, of course, multiply this out, but that's just an algebra exercise.

Example 2: Show that if  u(x) = C f(x)  (where C is any constant), then  u'(x) = C f'(x). 

This is just a the product of a constant function,  g(x) = C times f(x).  We know that the derivative of a constant function is always zero. So we can apply the product rule (equation 4.2-20b) to this, substituting C for  g(x)  and 0 for  g'(x).  

   u'(x)  =  (f'(x) C) + (f(x) (0) )
Of course the right-hand summand goes away because it is zero, and the commutative law of multiplication applies to the left hand summand, and so we've proved it.

Example 3: Show without using the binomial theorem (as we did in the last section), that if  u(x) = xn  and n is a counting number, then  u'(x) = nxn-1. 

The proof is by induction again. To get onto the first rung of the ladder, we set  n = 1.  So that makes  u(x) = x1 = x.  The derivative of that is an  mx + b  problem with  m = 1 and b = 0.  That means that if  n = 1,  then  u'(x) = 1.  That is consistent with  u'(x) = nxn-1.  So we're onto the first rung of the ladder.

Now we show that from the nth rung of the ladder we can get to the  n + 1st  rung. That means proving that if  u'(x) = nxn-1  for  u(x) = xn,  then it must follow that  u'(x) = (n+1)xn  for  u(x) = xn+1. 

We have 

   u(x)  =  xn+1  =  (x)(xn)
and that is a product of  f(x) = x  and  g(x) = xn.  We know that  f'(x) = 1,  and we have, by assumption of being on the nth rung, that  g'(x) = nxn-1. 

When you apply the product rule (equation 4.2-20b), you get: 

   u'(x)  =  ( (1) xn) + (x nxn-1)
When you do the algebra on that, you'll find that it simplifies to 
   u'(x)  =  (n+1)xn
That demonstrates that we can get from the nth rung of the ladder to the  n + 1st  rung, and that means we can get to any rung of the ladder with this formula.

Exercises

4) Apply the rules we have established so far (that is the sum rule, the product rule, along with the derived rules for differences and for multiplying by a constant, and the rule for finding the derivative of xn) to find the derivatives of the following. 

a)   u(x)  =  (m1x + b1) (m2x + b2)

b)   u(x)  =  (x2 + 2x + 1) (x2 - 3x + 2)

c)   u(x)  =  (x - 1) (4x4 - 7x3 + 2x2 - 5x + 8)

d)   u(x)  =  x2 f(x)

e)   u(x)  =  (x f(x) )  -  (x3 g(x) )
view answers

Return to Table of Contents

Move on to 4.3 More Rules to Live By

email me at hahn@netsrq.com