Karl's Calculus Tutor - Hero's Formula Derived

Hero's Formula DerivedKCT logo

© 1998 by Karl Hahn

Click here to go right to Hero's formula

Why We Need a Hero

The area of a triangle is one half base times height. We all remember that. But what do you do if you don't know the height? Euclid showed us 23 centuries ago that a triangle is completely determined by the lengths of its three sides. So if you know those lengths, you ought to be able to determine the triangle's area, right? But unless the triangle has a right angle in it, none of those three sides are its height. Then how do you find the area?

Hero to the Rescue

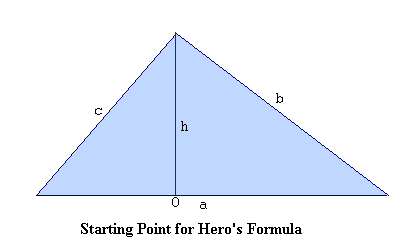
Triangle Diagram for Hero's Formula

Here is a diagram of a triangle with sides of length a, b, and c. The height is shown as length, h, and the point on the bottom where the height segment intersects the base at right angles is shown as point, O. In this case we have side a as the base, and more importantly, we have chosen the longest side as the base. Whether we know the height or not, by the formula we learned in grade school, we still have for area, A 

         1
   A  =    ah
         2
But the height, h, does remains unknown. We can involve sides b and c in this by observing that, according to Pythagoras, the length of the line segment to the left of O is sqrt(c2 - h2), and the length of the line segment to the right of O is sqrt(b2 - h2). Also, the side, a, which we have taken as the base, is equal to the sum of those two. So 
          _______    _______
   a  =  Öb2 - h2 + Öc2 - h2
If you square both sides of this, you get, after a bit of rearranging terms, 
                            ______________________
   a2  =  b2 + c2 - 2h2 + 2Öb2c2 - (b2 + c2)h2 + h4
But we still have a nasty square root term in there. To get rid of that, we move everything that is not the square root term over to the left, and then we square both sides again. 
   (a2 - b2 - c2)2 + 4(a2 - b2 - c2)h2 + 4h4  =  4b2c2 - 4(b2 + c2)h2 + 4h4
Notice that I did not multiply out the (a2 - b2 - c2)2 term. Indeed, I treated (a2 - b2 - c2) as if it were a single, indivisible term. There are two reasons for that. One is laziness. The other will become apparent shortly. But first, we get some marvelous cancellations in the above. The 4h4 terms both cancel. Also the -4b2h2 and the -4c2h2 terms all cancel, leaving only 
   (a2 - b2 - c2)2 + 4h2a2  =  4b2c2
Magically we are left with only a single term containing the unknown height, h. A slight rearrangement of this gives 
   4h2a2  =  4b2c2 - (a2 - b2 - c2)2
But recall that A = (1/2)ah. That means that the left hand term is simply 16A2. So what we really have is 
   16A2  =  4b2c2 - (a2 - b2 - c2)2
In other words, we have an expression here for sixteen times the square of the area. Not only that, the expression is the difference of squares, which means we can factor it easily. My prior laziness pays off. When you factor the above equation, you get 
   16A2  =  (2bc + (a2 - b2 - c2) )(2bc - (a2 - b2 - c2) )
Rearrange these terms and you get 
   16A2  =  (a2 - (b2 - 2bc + c2) )( (b2 + 2bc + c2) - a2)
Notice that the expressions involving b and c are both perfect squares. Hence this is the same as 
   16A2  =  (a2 - (b - c)2 )( (b + c)2 - a2)
and now we have two differences of squares, each of which we can factor further. 
   16A2  =  (a - (b - c) )(a + (b - c) )( (b + c) - a)( (b + c) + a)
You can see that if you divide both sides by 16, you will have the square of the area by itself on the left. But 16 = 24. So instead of dividing by 16, I will divide by 2 four times. And I will apply each division to one of the factors above. 
          (a - b + c) (a + b - c) (b + c - a) (a + b + c)
   A2  =                                                 
               2           2           2           2
which is a pretty good formula for a triangle's area given the lengths of its three sides. But Hero had one more trick up his sleeve. He said, let 
         (a + b + c)
   s  =             
              2
That is, s is equal to the last factor in the formula. If you do that, the other three factors become (s - b), (s - c), and (s - a) respectively. So the usual presentation of Hero's formula is 
          ______________________
   A  =  Ös(s - a)(s - b)(s - c)
In this form, it looks so simple. But it took a select sequence of algebraic manipulations to get here. And you'd never guess that somebody figured this out over 2000 years ago.

Return to Main Text

email me at hahn@netsrq.com