Section 5: Applications of Derivatives

5.1 Hilltops and Valley Floors

Since you began your study of calculus, have you ever thought to yourself, "If only I were a genius, this stuff would be a snap." Well I'd like to introduce you to a fellow who is a genius. He undoubtably learned calculus before he was out of puppy-hood.

	My apologies to Chuck Jones, the creator of Wile E. Coyote. If he or his copyright holders object to my usage of the character here, please contact me and I will remove it. The name, Wile E. Coyote, and the image of him are copyrighted trademarks of Warner Brothers, Inc.

How else would he be able to calculate exactly where the Acme anvil launched from an Acme catapult will fall, and place the bird seed at that very spot? And look where his genius has got him. Blown up, burnt to a crisp, run over by trains, trucks, buses, etc., crushed by boulders, shot by cannons, and fallen countless times off of cliffs. Better that you learn calculus the old fashioned way -- by working hard at it. You'll end up knowing it just as well as Wile E. Coyote here, but without the unintended side effects of being a genius.

There is something about Mr. Coyote, though, that is far more admirable than his genius. He never gives up, no matter how miserably and how many times he fails. If you emulate that one trait, you will end up learning this material. And that is the first lesson you can learn from him.

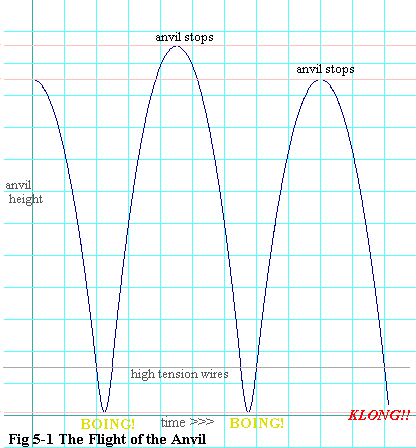
Here is another. Wile E. Coyote stands on a cornice at the rim of a canyon, holding an Acme anvil. Far below, a bridge spans the canyon. On it there is a pile of birdseed. The Roadrunner zips along, fit to cross the bridge in the blink of an eye. But he halts suddenly at the bird seed and begins pecking. This is Wile E's cue. He drops the anvil. It plummets down toward the unsuspecting Roadrunner, who, while the anvil is still falling toward him, has finished his snack. The Roadrunner zips off across the bridge and disappears in the distance. The anvil drops through the roadway, right where the Roadrunner was, leaving an anvil-shaped hole. It continues to drop until it encounters some high-tension electrical wires that run under the bridge. The wires stretch under the impact until the anvil is just inches above the ground. Then they spring back, catapulting the anvil straight up. It flies back up through the anvil-shaped hole in the bridge. It flies up past the cornice where Mr. Coyote still stands. It flies high above Mr. Coyote's head. Finally it runs out of steam and begins falling back down. This fact is not lost on Mr. Coyote, who now shields his head, for experience has taught him of the attractive power his head has for heavy objects. But to his joyous surprise, the anvil misses him. Instead it falls through the cornice, which cracks as a result and becomes free of the canyon rim.

I think you know the rest of this story. The cornice drops out from under Coyote. Coyote (still happy over avoiding the all too familiar sensation of anvil versus carnivore skull) somehow ends up traveling downward beneath the falling cornice. Coyote leaves a coyote-shaped hole in bridge, which soon becomes a cornice-shaped hole. The anvil bounces again on the wires. Coyote is not so lucky. The wires try to mitigate his fall, but unfortunately he ends up wedged between the wires and the massive cornice. But not for long. The squeeze has the effect of causing Coyote to arrive at the canyon floor in slices. By some miracle he is able to pull himself together from this mishap just in time to be struck on the head by a falling anvil. And of course, in his daze, he is unaware that he now stands in the rapidly expanding shadow of a falling cornice.

What on earth, you are probably wondering, does any of this have to do with calculus? Well, I'd like you to focus your attention on the flight of the anvil. At what times other than before Coyote releases it and after it arrives on top of his head is the anvil at a standstill? When the anvil reaches the wires the first time, the wires stretch, slowing the anvil down. According to the story, just inches from the ground the anvil turns around and begins traveling up instead of down. Then it flies up, finally losing steam high in the air, and it turns around and drops back down. At each of those turn-around moments (and at the other two times it turns around), isn't the anvil stopped for an instant? In fact, isn't it impossible to reverse direction without stopping for just an instant?

We call such moments when the anvil is stopped momentarily in flight, stationary points or critical points.

And notice another thing. At the moment the anvil turned around on the wires -- just inches above the ground -- wasn't it as low as it was going to go (at least on this leg of its flight)? And at the moment it turned around high over Coyote's head, wasn't it as high as it was going to go? And when you walk down a wooded path and finally get tired and stop, then turn around and walk back, isn't that as far as you are going to go into the woods (at least on that walk)?

There are two points here. One is that to reverse direction, you must stop for at least an instant. The other is that when you do reverse direction, you are as far in one direction as you are going to get -- at least until you've turned around again. And that is the essence of what this section is about.

So in the case of the anvil, you can look for when it is as high as it will go and as low as it will go by looking for the moments at which it is stopped. And stopped means its speed is zero. And isn't speed the derivative of its position with respect to time? So to find the moments that the anvil is at its extreme positions, we look for the moments at which the derivative of position is exactly zero. And that is the definition of a stationary or critical point (the two words are synonymous). We have a stationary or critical point of a function whenever its first derivative is zero.

At stationary (or critical) points is where we look for a function to attain an extreme. That is the function is likely to be momentarily as big as it will get (locally) or as small as it will get (locally). In other words, it is likely to reach either a local maximum or a local minimum.

Note: The word you may have already encountered in class, extrema, is nothing more than the Latin plural of the word, extreme. Likewise maxima and minima are the Latin plurals or maximum and minimum respectively).

Let's take a simple example of a problem we can solve using this method. Consider the function,  f(x) = x² + 1. We already know by looking at the graph that it has its minimum value of  f(x) = 1  at  x = 0. So how does our new insight into the behavior of derivatives at maximums and minimums jibe with this? Well, taking the derivative of  f(x) = x² + 1  we have  f'(x) = 2x. We know that when f(x) is at a maximum or a minimum, f'(x) should be zero. So at what x is f'(x) equal to zero? The only place that can happen is at  x = 0. So this confirms what we already knew about f(x), that is that its minimum is at  x = 0. That tells us where the minimum of f(x) is. To find what the minimum is, we substitute the where in for x into f(x). In this case the where is zero, and  f(0) = 1.

Let's try a harder example. Suppose we have 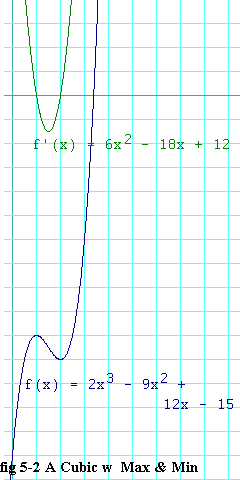 f(x) = 2x³ - 9x² + 12x - 15, and we wanted to know the maximums and minimums. You should note, first, that this f(x) gets as large as you like if you pick x large enough and it gets as small as you like (that is as negative as you like) if you pick x negative enough. So there is no global maximum or minimum. But, as we shall see, there is local a maximum and a local minimum.

But what do we mean by a local maximum or minimum? Well look back at the flight of the anvil graph in figure 5-1. The second "hump" is not as high as the first, so the second hump cannot possibly be a global maximum. But it is a local maximum. Why? At that point the anvil is higher than it is either immediately before of immediately after the hump.

Of course that wording is not rigorous enough to write on an exam. So here is the rigorous wording that means the same thing. If a function, f(x), has a local maximum at x = a, then there is an open interval containing a such that for every x on that interval,  f(x) £ f(a). In mathematical parlance, such an interval containing a point, a, is called a neighborhood of a. Neighborhoods can be big or small. What the above wordplay about local maximums means is simply that if x = a is a local maximum of f(x), then there is a neighborhood of a small enough so that f(x) does not exceed the maximum anywhere in that neighborhood.

You can come up with a similar definition for local minimums, and that is an exercise I'd like you to try.

Let's get back to  f(x) = 2x³ - 9x² + 12x - 15. Look at the graph of it shown in figure 5-2 (the blue trace). Can you see any local maximums or minimums in the graph? How do you suppose you would go about finding the exact coordinates of any local maximum or minimum you might find? Take out a pencil and paper and see if you can work this out for yourself. Refer to the green trace in figure 5-2 to see how the derivative of the blue trace behaves. Look at what the green trace does at the same x-values the the blue trace is at a local maximum or minimum. When you are done, or if you get hopelessly stuck, click here for details.

You should by now have observed that both the local maximum and local minimum of the blue trace occur at the same x-values as where the green trace (which is the derivative of the blue trace) crosses the x axis. Not only that, if you were especially observant, you would have noticed that the local maximum of the blue trace occurs where the green trace crosses the x axis going down (as you scan left to right), and the local minimum occurs where the green trace crosses the x axis going up. In fact, this is how you can tell local maximums from minimums without having to make a graph.

But how can you tell whether the derivative is crossing going up or down without having to graph it? Simple. Find the derivative of the derivative. Where the derivative is sloping down, the derivative of the derivative will be negative. Where the derivative is sloping up, the derivative of the derivative will be positive.

The derivative of a derivative is something that comes up all the time in calculus. So naturally, it has a name. The derivative of the derivative of a function, f(x) is called the second derivative of f(x), and is indicated by the symbol, f"(x).

In this case we have the derivative given by  f'(x) = 6x² - 18x + 12. To find the second derivative of f, we apply the rules for taking derivatives a second time. What we get is  f"(x) = 12x - 18.

Now observe that if we take out two stationary points,  x = 1  and  x = 2  and substitute them into f"(x) we get  f"(1) = -6  and  f"(2) = 6  respectively. So even if I had never seen the graph of  f'(x) = 6x² - 18x + 12 , I could still know that is sloped down at  x = 1  and sloped up at  x = 2 . Why? Because f"(x) is negative at  x = 1  and f"(x) is positive at  x = 2.

This rule on how to distinguish local maximums from local minimums is useful enough that you should memorize it. But, as always, it is even more useful to know why it works. Let's go back to Mr. Coyote's anvil. Here again is the graph of that. Will you agree that I should call up the positive direction and call down the negative direction, as is illustrated on the graph? So when the anvil is traveling up, its velocity is positive and when it is traveling down, its velocity is negative. And remember that velocity is the derivative of the blue trace in this graph (figure 5-1).

Remember, the anvil's velocity is the derivative of its position.

So the anvil starts out with negative, that is to say a downward velocity. Let's say that when it reaches the wire, the anvil is going 100 meters per second downward, or in other words,  v(t₀) = -100 meters/sec  at moment it makes contact with the wires. We know that shortly after that the anvil will be going  v(t₁) = 0 meters/sec. We know that because we know that the wires actually stop the anvil for an instant in order to turn it around. From the time the anvil makes contact with the wire until the wire stops it, its net change in velocity is  v(t₁) - v(t₀) = 0 - (-100) meters/second. So the net change is 100 meters per second, which is positive. Then right after the anvil stops, it begins traveling upward, that is, its velocity becomes positive. Let's say that when it leaves the wire it is traveling 100 meters per second upward, or  v(t₂) = 100 meters/sec. Again the net change in velocity from the time the anvil stopped until it leaves the wire is  v(t₂) - v(t₁) = 100 - 0 meters/sec.

In fact, the whole time the anvil is in contact with the wires, its velocity is becoming progressively greater (at first by becoming less negative, and then by becoming more positive). In other words, the velocity's change is positive throughout that time. But that is just another way of saying the velocity's derivative is positive. And the velocity's derivative is the same as the second derivative of the anvil's position.

But if the anvil was moving down before it hits the wires and is moving up after it hits the wires, it must have been at its minimum height some time while it was in contact with the wires, that is during that same time when the derivative of its velocity (that is when the second derivative of the anvil's position) was positive

See if you can make a similar verbal analysis on the anvil's motion as it soars back up after springing from the wires, being slowed down as it goes by toon-gravity (whose physics is known but to animators). Describe what happens at the peak of the anvil's trajectory. How does this confirm the rule we have for maximums?

Summary of Maximum and Minimum Introduction

1) Local maximums and minimums of a funtion, f(x), often (but not always) occur at stationary points where the function's derivative, f'(x), is zero.

2) You can determine whether a stationary point is a maximum or a minimum by using the following rule: If the second derivative of f(x), that is, f"(x) is negative at the stationary point, then that stationary point is a maximum. If the second derivative is positive at the stationary point, then the stationary point is a minimum. We shall cover the case of the second derivative being itself zero at the stationary point in the next section.

3) You can solve for the x-values of stationary points by setting the derivative to zero and finding what x-values satisfy the resulting equation.

4) You can find the y-values of the stationary points by substituting the x-values you got from summary-point 3) into f(x).

5) This stuff will be on the exam.

                 1
   f(x)  =             
            x2 - 2x + 2

3b) Find f"(x) and use it to discover whether the stationary point is a maximum or minimum. Hint: You will have to apply the quotient rule again to do this.

4) Three sides of a window frame form three of the sides of a rectangle. The fourth side is a semicircle. The perimeter of this shape is fixed at 3 meters. Find the dimensions that maximize the area enclosed. Also determine what the maximized area is.

5) Find the point(s) on the curve, y = x² + x + 1 that is closest to the point, (-1, 2). Hint: Use the Pythagorean formula for distance to find a function that relates the x coordinate of a point on the curve with the distance of that point to (-1, 2), and find the x that minimizes that functions. Another Hint: Observe that if you minimize the square of the distance, you also minimize the distance.

6) If a triangle has sides of length a, b, and c, then Hero's Formula enables you to find the area of the triangle without knowing its height. The formula says to set

         a + b + c
   s  =           
             2

          ______________________
   A  =  Ös(s - a)(s - b)(s - c)

7) No tutorial on maxima-minima problems would be complete without an economics problems. Suppose you are in the business of manufacturing and selling bowties. Your marketing research indicates that the number of bowties you will sell each month is related to the price you charge, x, according to the function:

   n(x)  =  40000 - 800x

8) Rosie O'Donnell is swimming 50 meters from the shore. When she looks up she sees Tom Cruise standing at water's edge 100 meters down the beach from where Rosie is swimming. If you have watched Rosie's television show, you know that she has a thing for Tom Cruise. Rosie's top speed swimming is one meter per second. Her top speed running is 4 meters per second. What point on the beach should she swim for in order to minimize her time to reach Tom Cruise?

View Answers

Return to Table of Contents

Move on to 5.2 Squigglies, Wormtails, and Pointed Little Heads

email me at hahn@netsrq.com

Return to main text

   f'(x) = 6x2 - 18x + 12                                            eq. 5.0a-1

   6x2 - 18x + 12 = 0                                                eq. 5.0a-2

Return to main text