Box 4.1 Coached Exercise: Finding a DerivativeKCT logo

© 1996 by Karl Hahn

Derivatives of Powers of x

The problem is to apply equation 4.1-2 in order to find f'(x) when f(x) = x2. So that you won't have to flip back and forth, here is 4.1-2 again: 

             df             f(x + h) - f(x)
   f'(x)  =      =    lim                                        eq. 4.1-2
             dx      h  > 0        h
You should know what the function, 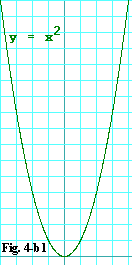f(x) = x2, looks like, but in case the memory has grown dim on you, figure 4-b1 shows a graph of it. graph of x squared Notice that to the left of the y-axis the graph slopes down. To the right of the y-axis it slopes up. Where it crosses the y-axis, it appears to be level, that is it appears to have zero slope. Whatever expression you arrive at for the derivative, f'(x), of this function ought to be consistent with all three of those facts. So it ought to be negative whenever x is negative, it ought to positive whenever x is positive, and it ought to be zero either at or very near where x = 0. So you can use these tests to check your work when you're done.

Step 1: Write expressions for f(x) and f(x + h), because that is what you need to plug into 4.1-2.

Step 2: Rewrite equation 4.1-2, but substitute your expressions for f(x) and f(x + h) for where they are shown in 4.1-2.

Step 3: One of the expressions can be multplied out into an expanded form. Rewrite the equation again using the expanded form.

Step 4: You should see a cancellation you can take in the numerator of the of your equation. Cancel it and rewrite the equation in the simplified form.

Step 5: Do you have a quotient of polynomials in h? If so, you can use the rule we discovered in section 2.5 to take the limit. Rememeber, find the lowest power of h whose numerator and denominator coefficients are not both zero. The ratio of those coefficients is your limit. And remember that a coefficient can be an expression involving x, but a coefficient cannot be an expression involving h. Why? Because we are dealing with polynomials in h. Furthermore, when you take the limit as h goes toward zero (or toward anything else, for that matter), you should always end up with an expression that contains no h's.

And if you don't have a quotient of polynomials in h then go back and check your work. You probably made an algebra mistake somewhere.

Does the expression you have derived for f'(x) conform with the rules we said it should just a few paragraphs back? Is it positive wherever x is positive, negative wherever x is negative, and either zero or close when x = 0? If not, check your work and try to ferret out the mistake.

If it does conform, then try one more check. Use your expression for f'(x) to find actual values of the derivative at x = 1 and x = 2. Hold a straight edge up to the screen so that it is tangent to the curve in figure 4-b1 at each of those x values. Eyeball the straight egde against the graticule in the graph and try to estimate its slope. Are the slopes you come up with that way consistent with the the ones that come out of your version of f'(x)?

If you were unable to get through any step, go back to section 4.0 and review the method we used to find the exact grade of the animal's wall at any point. Then return here and try this exercise again.

Finding the Derivative of g(x) = xn

In order to find this derivative, we will be using the binomial theorem. You probably covered it in algebra, but it is worth reviewing once again. The binomial theorem gives you a formula for expanding the expression (u + v)n, where n is a counting number. The binomial theorem expands it to an expression in the form of: 

   (u + v)n  =  b0unv0 + b1un-1v1 + b2un-2v2 + ... + bn-1u1vn-1 + bnu0vn

                                                                 eq. 4b-1
I know that thing in equation 4b-1 looks pretty nasty, but don't panic. It is simply the sum of n + 1 terms, each of which is the product of three things: a coefficient, bk, a power of u, and a power of v. Notice that the sum of the two powers in each term is exactly n. Of course the real trick here is to figure out what the exact values of the coefficients, bk, are.

You will remember from algebra that anything to the zero power is 1, and anything to the first power is itself.

Do you remember how the counting numbers are like ladder? If you can get to the first rung, and if from any rung you can get to the next rung, then you can get to any rung. That is how we will approach the binomial problem.

The first rung is where n = 1. And it is our good fortune that the first rung is an easy one. 

   (u + v)1  =  u + v  =  (1)u1v0 + (1)u0v1                      eq. 4b-2
This does seem to agree with equation 4b-1. It has n + 1 terms (that is to say it has 2 terms), the sum of the exponents in each case is n, and we have found that b0 = b1 = 1.

Now let's see what happens if we are poised on the nth rung of the ladder and we try to climb to the n + 1st rung. Remember that if we can show that we can get onto the first rung of the ladder with 4b-1 (which we have already shown) and if from any rung where 4b-1 holds we can get to the next rung and show that it must hold there also, then it must hold for all rungs of the ladder. That is proof by induction. For the n + 1st rung, we have: 

   (u + v)n+1  =  (u + v) (u + v)n                               eq. 4b-3
On the right hand side of 4b-3 we can see that one of the factors is the same as the left hand side of 4b-1 as it applies to the nth rung of the ladder. Since we are assuming that 4b-1 already holds for that rung (because we are trying to show that 4b-1 holds for the n + 1st rung whenever it holds for the nth rung), we can go ahead and substitute from 4b-1 into 4b-3: 
   (u + v)n+1  =

       (u + v) (b0unv0 + b1un-1v1 + b2un-2v2 + ... + bn-1u1vn-1 + bnu0vn)

                                                                 eq. 4b-4

By multplying through first by u, then by v, and then gathering up terms of like powers into columns, we get: 

   (u + v)n+1  =

      b0un+1v0 + b1unv1 + b2un-1v2 + ... + bn-1u2vn-1 +   bnu1vn +
                b0unv1 + b1un-1v2 + ... + bn-2u2vn-1 + bn-1u1vn + bnu0vn+1

                                                                 eq. 4b-5
All the terms that derived from multiplying by u are in the first line after the equal sign; all the terms that derived from multiplying by v are in the second line after the equal sign. They are lined up according to like powers.

First, notice that we are definitely going to get different coefficients for the n + 1st rung than we did from the nth rung. Look at 4b-5 carefully. The bk terms are the coefficients for the nth rung of the ladder. If you use the symbols, b*k, to indicate the coefficients that we will find in the n + 1st rung of the ladder, then: 

   b*0    =    b0                                                eq. 4b-6a

   b*n+1  =    bn                                                eq. 4b-6b
and for all the subscripts in between: 
   b*k    =    bk-1 + bk                                         eq. 4b-6c

What we have shown so far is that 4b-1 holds for all counting numbers, n, except with a different set of coefficients for each n. We also know exactly what the coefficients are for n = 1. And we have formulae that give you the coefficients for n + 1 given that you already know the coefficients for n.

Using that knowledge, we can develop a table of binomial coefficients:

Table 4b-1: Binomial Coefficients (n £ 12) 
  n:      b0   b1   b2    b3   b4   b5   b6    b7   b8   b9   b10  b11   b12
  1:       1    1
  2:       1    2    1
  3:       1    3    3    1
  4:       1    4    6    4    1
  5:       1    5   10   10    5    1
  6:       1    6   15   20   15    6    1
  7:       1    7   21   35   35   21    7    1
  8:       1    8   28   56   70   56   28    8    1
  9:       1    9   36   84  126  126   84   36    9    1
 10:       1   10   45  120  210  252  210  120   45   10    1
 11:       1   11   55  165  330  462  462  330  165   55   11    1
 12:       1   12   66  220  495  792  924  792  495  220   66   12    1

You can see for yourself how table how the table was formed. We know the first line, when n = 1, because those coefficients dropped into our lap in equation 4b-2. In all subsequent rows, where n > 1, equation 4b-6a shows that we simply get the b0 for the next line by copying the one from the last line. Since the first line has b0 = 1, so must every other line. We can apply 4b-6b in the same way to determine that the last entry in each line must also be 1. Equation 4b-6c gives us a rule for finding all other entries. To find an entry in the table, simply go to the previous row and add the entry directly above the one in question with the one just to the left of that. For example, in entry b3 of the tenth row we have: 120 = 36 + 84. As an exercise, try generating the first few entries for the thirteenth line of this table.

There is more to know about binomial coefficients, and you can (and should) learn it by clicking here.

But for the purposes of finding the derivative of g(x) = xn, we will need to know only how to calculate the values of b0 and b1 of the nth row of the table. We have already established that b0 is always 1. If you look at the b1 column of table 4b-1, you can see that it simply counts up from 1. And it's easy to see that it must do that for every row of the table -- it follows from equation 4b-6c and from knowing that b0 always 1. So clearly, b1 of the nth row of the table is always equal to n.

So, with our knowledge of binomial coefficients in place, let's now procede to finding the deriviative of g(x) = xn using equation 4.1-2 (except this time we use g(x) instead of f(x)).

Step 1: Find expressions for g(x) and g(x + h). The expression for g(x) is given by the problem: g(x) = xn. The expression for g(x + h) is (x + h)n (found by substituting x + h in for x into the expression for g(x)).

Step 2: Substitute those expressions into 4.1-2 in place of f(x) and f(x + h) respectively: 

                    (x + h)n - xn
   g'(x)  =   lim                                                eq. 4b-7
             h  > 0       h

Step 3: Apply the binomial theorem to (x + h)n. That is, expand that expression using the formula given in 4b-1. And remember that we already know the values of b0 and b1. So in our expansion, we can show those values, then use b-symbols for all the rest. 

                    1xnh0 + nxn-1h1 + b2xn-2h2 + ... + bn-1x1hn-1 + bnx0hn - xn
   g'(x)  =   lim                                                            
             h  > 0                          h

                                                                eq. 4b-8

Step 4: Take the cancellation. Notice that 1xnh0 is the same as the xn at the end of the numerator, except that it is multiplied by some things that are each equal to 1. Hence, 1xnh0 = xn, and you can cancel those two terms: 

                    nxn-1h1 + b2xn-2h2 + ... + bn-1x1hn-1 + bnx0hn
   g'(x)  =   lim                                                 eq. 4b-9
             h  > 0                     h

Step 5: Use the rule to take the limit. The rule we discussed in section 2.5 applies here because we have a polynomial in h in the numerator and a polynomial in h in the denominator. The polynomial in the numerator has 1 as its lowest power of h and the coefficient of that term is nxn-1. The polynomial in the denominator has only one term, and it has a coefficient of 1 and a power of 1 (remember that h1 is the same as h). At least one of the coefficients is not zero. So the rule says that the limit is the quotient of these. 

   g'(x)  =  nxn-1                                               eq. 4b-10
According to the rule from section 2.5, all the higher power terms of h (that is with exponents of 2 or greater) with all their bk coefficients (that we didn't bother to attach values to) make not a bit of difference when you take the limit as h goes toward zero. In the limit, they all drop away. Why? Because the lowest power in the denominator is 1. All the numerator terms with greater power than that don't do squat in the limit.

The fact that the derivative of xn is always nxn-1 is worth memorizing because it comes up often. But don't go forgetting how it is derived. And remember too that this derivation applies only to the case where n is a counting number.

And what, you might ask, about the case when n is not a counting number. What if it is a fraction, such as 1/2 (note that x1/2 = sqrt(x))? Does 4b-10 work on that as well? Actually, it does, and we will be getting to that in the next section. However, I have seen math instructors who have students work out the deriviative of f(x) = x1/2 by giving them a version of the binomial theorem that applies to non-counting number values for n. If your instructor does this, he or she deserves to be strongly challenged. There are several reasons. First, we shall shortly see that there is a much easier way to come up with the derivative for that function. Second, that version of the binomial theorem (that is the version where n is a fraction) can only be proved if you already know the derivative of xfraction. Third, that version of the binomial theorem gives you a sum of an infinite number of terms, and there is no reason to believe, without proof, that they add up to any finite value. In fact, for a wide domain of x's, they don't.

Exercises

Use the formula given in 4b-10 to find the derivatives of the following: 

   f(x)  =  x3

   f(x)  =  x4

   f(x)  =  x5
When you're done, try plugging each of these functions into the limit formula given in 4.1-2. Expand each using the binomial theorem (you can copy the binomial coefficients you need from table 4b-1 if you like), then take the limit using the rule from section 2.5. This set of derivatives ought to agree with the first (i.e. the ones you got by applying 4b-10).

Return to Main Text

email me at hahn@netsrq.com