Box 8.4-1: Bounding the Error Term

How We Get Equation 8.4-3

This is optional material

No matter what function f(x) is, it is always true that

   f(c + h)  =  f(c) + hB                                         eq. 8.4-4

for some real number, B. Indeed you can always find B if you know f(c) and f(c + h).

   f(c + h) - f(c)
                    =  B                                          eq. 8.4-5
          h

But we don't know the value of f(c+h). That is why we are trying to approximate it.

Surely you recognize the quotient in equation 8.4-5 as the same one we take the limit of to find f'(c). The question is, how much different is B from f'(c)?

The Mean Value Theorem requires that B = f'(b) for some b that lies between c and c+h. So if you had used

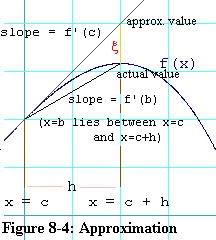
   f(c + h)  =  f(c) + hf'(b)                                     eq. 8.4-6a

as the approximation formula, the approximation would have been perfect. Figure 8-4 shows how the tangent line with a slope equal to f'(c) yields an approximation to f(c+h), but the darker line -- the one that intersects f(x) in two places -- finds the exact value of f(c+h). That line has a slope of f'(b). The little red x shows the difference between the approximate and actual values of f(c+h). You should be able to see from the graph that

   |x| = |(f'(c) - f'(b)) h|                                      eq. 8.4-6b

Since the word, "mean," in "Mean Value Theorem" is just another word for "average," f'(b) is simply the average of f'(x) over the interval from c to c+h. So what the equation is saying is: The error, x, in the approximation will be the length of the interval, h, times the difference between f'(c) and the average value of f'(x) over the interval, which is to say, f'(b).

The problem is that we have no way of knowing exactly what b is or what f'(b) is. But we do know that b differs from c by no more than h. How much can f'(x) change when x is confined to the interval of real numbers from c to b?

The way to answer that is to ask, at what rate is f'(x) changing at x = c? That rate is given by the second derivative, f"(c). Of course f"(x) may not be constant throughout the interval from c to c+h. So now we ask, what is the worst it can do to change f'(x)? If we find that, then at least we can bound how much inaccuracy we introduce by using f'(c) instead of f'(b) in the approximation formula.

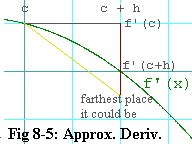
The worst that f"(x) can do to alter f'(x) is where |f"(x)| is maximum in the interval from c to c+h. Figure 8-5 shows the derivative of the f(x) shown in figure 8-4. The slope of the yellow line is equal to worst value f"(x) has on the interval. Notice that the green trace of f'(x) stays inside the triangle over the entire interval, c to c+h. It has to because the hypotenuse slopes down at least as steeply as the green trace does anywhere on the interval. Indeed we chose the slope of the hypotenuse to do just that.

It is the Extreme Value Theorem that guarantees us that f"(x) has a point, x = a, where its magnitude, |f"(a)|, reaches its maximum over the interval, c to c+h. In other words, there will be a real number, a, between c and c+h where we can say that over the entire interval, [c,c+h], f'(x) changes at a rate no greater than |f"(a)|.

That means that the most that f'(x) can change over the interval is hf"(a). In figure 8-5 you can see that the vertex of the yellow and brown lines is the farthest that f'(x) can possibly get from f'(c) in the interval from c to c+h.

But we are not interested in the farthest that f'(c) is off by. In most of the interval it's not nearly that bad. Indeed at x = c it's perfect. We are really interested in the average by which f'(c) differs from f'(x) in the interval.

We can't know that average exactly, but we can know the average by which f'(c) differs from the yellow line in figure 8-5. And because the green trace stays inside the triangle throughout the interval, the average difference between f'(c) and f'(x) will be no worse than the average difference between f'(c) and the yellow line. That average is going to be half the height of the triangle, which is

   1
     |hf"(a)|                                                     eq. 8.4-7a
   2

But f'(c) is constant. So the average difference between f'(c) and f'(x) is the same as the difference between f'(c) and the average of f'(x). And the Mean Value Theorem has already told us that the average of f'(x) over the interval is f'(b). So

                        1
   |f'(c) - f'(b)|  £     |hf"(a)|                                eq. 8.4-7b
                        2

Recall from equation 8.4-6b that |x| = |(f'(c) - f'(b)) h|. Multiplying both sides of equation 8.4-7b by |h| and substituting gives the bound on the error term, x:

          1
   |x|  £    |h²f"(a)|                                            eq. 8.4-3
          2

Return to Main Text

email me at hahn@netsrq.com