Section 5: Applications of Derivatives

5.4 Like a Steam Locomotive (Rolle's Theorem)

Once again I ask you to journey in time back to the old west and take a train ride. On a particular day in 1888, a Union Pacific train left the station in Denver at noon bound for San Francisco. But before departing, the switch-yard workers coupled to it the private car of one J. Morgan Prescott, owner of banks, railroads, cotton mills, and coal mines. Two words that describe him best are tycoon and temperamental. For they weren't but ten minutes out of the station when Mr. Prescott asked his valet for a glass of Napoleon Brandy. When the valet returned moments later with a glass of lesser brandy, Prescott sniffed at it and exclaimed,

"What manner of tomfoolery is this? I asked you for Napoleon Brandy. Did you even look at the label?"

"Yes sir. But the only brandy on this train is from Seneca Falls, New York."

"And did I not ask you to purchase Napoleon Brandy while we were in Denver?"

"I tried, sir. The wine merchant promised me it would be here, but his man failed to show up before the scheduled departure."

"Well," thundered Prescott, "I suppose I'll have to fix this situation myself." And with that he stormed out of his car and didn't stop till he had reached the engine.

"Get back to your seat, sir," said the engineer. "You really shouldn't be here."

"Don't give me any lip. I'm a major stockholder in this railroad. Get this train on its way back to Denver this instant!"

"But sir..." the engineer began. But Prescott gave him such a scowl that the frightened engineer turned to his brakeman and signaled him to begin applying the brakes.

"Don't bother stopping," shouted Prescott. "That takes way too long. I want this train heading for Denver right now."

Surely you recognize the absurdity of Mr. Prescott's demand. But what is it that makes the thought of the train, cruising at say 30 miles per hour, instantly reversing its direction seem absurd? It is this: both the distance the train is from the Denver station and the train's speed are continuous functions of time. We shall assume that there are no loops in the track that the train can turn around on. If it is to get back to Denver, it must do so going backward on the same track it left Denver on. It seems common sense that for a train that left the Denver station to get back to the Denver station, it would have to stop, at least momentarily. This is the essence of a principle called Rolle's Theorem.

Rolle's Theorem says this: if you have a function, f(x), and you have two points, a and b (we shall assume that a < b) such that f(a) = f(b), and both f(x) and f'(x) exist and are continuous on the entire interval, a £ x £ b, then there must be a point, c lying between a and b where f'(c) = 0.

Read it over a few times to make sure you understand what it is asserting. Notice that the continuity requirements are on an interval that includes the endpoints, a and b -- that is a closed interval.

In the case of the train, we know that at noon (so let a be noon), the train was at the Denver station. Mr. Prescott would like it to be there again at some time in the immediate future (so let b be that time). If f(t) is the distance the train is from the Denver station as a function of time, t, then Mr. Prescott is demanding that f(a) = f(b) when he insists that the train get back to Denver, where it was just minutes before. And nature demands that both the train's distance from the station, f(t), and the train's speed, f'(t), be continuous functions of time. Rolle's theorem then demands that at some time, c, between when the train left Denver station and when it returns, f'(c) = 0, which is to say that at time c, the train must be stopped.

Another way to put Rolle's Theorem, if you'll forgive me for mangling a Grateful Dead lyric is:

Like a steam locomotive rollin' down the track,
If a function don't stop, it ain't never comin' back.

That lyric is, of course, subject to the continuity requirement stated previously -- trouble is the word "continuous" doesn't fit easily into a song lyric.

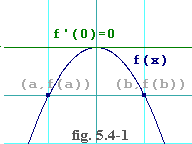
Figure 5.4-1 gives you a picture of what's going on. The blue trace shows a function. At points a and b, the function yields the same value, that is, f(a) = f(b). You can see that there is a point where f'(x) = 0 (at the middle of the graph). I have included a horizontal tangent line in green to illustrate that the derivative is indeed zero at that point.

Proof of Rolle's Theorem

There is a possibility that you will be asked to prove Rolle's theorem on an exam. Its proof follows easily as a consequence of two other theorems -- The Extreme Value Theorem and the Intermediate Value Theorem. You don't need to know the proof of The Extreme Value Theorem (unless your instructor has, in his or her cruelty, said you need to know it), and you probably don't need to know the proof of the Intermediate Value Theorem either, but you do need to understand what each of them asserts.

The Extreme Value Theorem asserts that if a function is continuous over a closed interval, it has a maximum and a minimum on that interval. In other words, there is an x_max on the closed interval where f(x_max) gives you a value that is never exceeded for any x on the closed interval. Likewise there is an x_min where f(x_min) is such that f(x) never goes lower than that for any x on the interval.

The Intermediate Value Theorem asserts that if a function, f(x), is continuous on the interval, a £ x £ b, then you can choose any y on the interval, f(a) < y < f(b), and there is guaranteed to be a solution to f(x) = y for some x on the interval, a < x < b.

In the case of Rolle's Theorem, both f(x) and f'(x) are presupposed to be continuous over a closed interval, a £ x £ b. So The Extreme Value Theorem applies to f(x), and The Intermediate Value Theorem applies to f'(x). In addition, Rolle's Theorem presupposes that f(a) = f(b).

If f(x) is constant, then f'(x) is zero everywhere. So Rolle's Theorem is trivial for constant functions.

We prove the case for nonconstant f(x) in a manner popular with mathematical proofs. We shall assume the opposite of Rolle's theorem and derive a contradiction.

Suppose that f'(x) is nonzero everywhere on the closed interval. Then The Intermediate Value Theorem makes it clear that if f'(x) is greater than zero anywhere on the closed interval, it must be greater than zero everywhere on the closed interval. Why? Because if f'(x) changes sign anywhere on the closed interval and is continuous, The Intermediate Value Theorem says that there must be an x that makes f'(x) be zero. And we have supposed that it is not zero anywhere. You can make the identical argument to show that if f'(x) is less than zero anywhere on the closed interval, it is less than zero everywhere on the closed interval.

If f(x) is not constant then it has at least one point at which it is different from f(a) and f(b). If f(x) is greater than f(a) and f(b) at such a point, then we know that f(x)'s maximum (which it must have due to The Extreme Theorem) cannot be at either of the end points. Call that point, x_max.

If f'(x) is greater than zero everywhere on the closed interval, then f(x) must be increasing everywhere on the closed interval, including at x_max. But if it's increasing, then for x's that are just a little greater than x_max, it must be true that f(x) > f(x_max). Yet f(x_max) was supposed to be the maximum of f(x) on the closed interval. That is the contradiction you get if you allow f'(x) to be greater than zero anywhere and nonzero everywhere.

Likewise if f'(x) is less than zero everywhere on the interval, then f(x) must be decreasing everywhere on the closed interval, including at x_max. But if it's decreasing, then for x's that are just a little less than x_max, it must be true that f(x) > f(x_max), and the same contradiction arises as before.

Since f'(x_max) cannot be positive or negative, it must therefore be zero. That proves the theorem if there is any f(x) on the closed interval that is greater than f(a) and f(b). The logic for showing what happens if there is an f(x) on the closed interval that is less than f(a) and f(b) is nearly identical, except that you compare everything to the point, x_min, where f(x) is minimum.

So no matter what, there must be an x between a and b where f'(x) = 0.

Main Points of the Proof

Again I have been wordier than you need to be on an exam. The main points are

The Intermediate Value Theorem tells you that if f'(x) is nonzero everywhere on the interval and is continuous, it cannot change sign on the interval.
The Extreme Value Theorem (and here you must use the name for this theorem that your instructor uses) guarantees that a continuous f(x) has a maximum, f(x_max), and a minimum, f(x_min), on the closed interval.
If f'(x) cannot be zero, then it means that f(x) is increasing or decreasing at both x_max and at x_min. That implies that f(x_max) and f(x_min) are not the maximum or minimum. And that is the contradiction that proves the theorem.

Note that some textbooks provide less rigorous (and shorter) proofs than the one I have given here. So check your textbook. If a shorter proof is given there, then I recommend that it be the one you reproduce, if asked, on the exam.

Rolle's Theorem over an Open Interval

There is one more point to make, which could come up on an exam, although I consider it to be more advanced than is suitable for first year students. Rolle's theorem is also true if f'(x) is continuous only on the open interval (remember that an open interval doesn't include the end points). Note that f(x) must still be continuous on the closed interval. An example of such a function is:

             ______
   f(x)  =  Ö1 - x²

and applying the chain rule to find its derivative, we get

               -x
   f'(x)  =         
             Ö1 - x²

where the endpoints are x = -1 and x = 1. Note that in this case, f(x) is continuous over the entire closed interval, but f'(x) is undefined at the endpoints and therefore continuous over only the open interval.

The proof of Rolle's Theorem when you allow f'(x) to be discontinuous at the endpoints is a little more difficult. It relies on the fact that if f(x) is nonconstant, then either x_max or x_min must be an interior point of the interval (that is, not an end point). It also relies on the fact that The Intermediate Value Theorem applies to f'(x) over every closed interval that is contained in the open interval. If f'(x) is continuous and never zero on the open interval, then The Intermediate Value Theorem still forces it either to stay positive over the entire open interval or to stay negative over the entire open interval. Why? Because it must do so over every closed interval that is contained in the open interval, and those closed intervals can take you as close to the end points as you like. So f(x) must still be increasing or decreasing at either x_max or x_min, whichever is the interior point. That still leads to the contradiction if you allow neither f'(x_max) nor f'(x_min) to be zero.

For a brief biography of Rolle click here.

The Mean Value Theorem

The Mean Value Theorem follows immediately from Rolle's Theorem. It says, in essence, if you drive 60 miles in 1 hour, then at some moment you must have been driving exactly 60 miles per hour. You may have been driving slower sometimes and faster others. You may even have stopped for coffee. But at some moment in that hour, you were going 60 miles per hour -- guaranteed.

The formal statement is this: If f(x) and f'(x) are continuous over a closed interval, a £ x £ b, then at some point, x_mean, where x_mean lies between a and b,

                 f(b) - f(a)
   f'(x_mean)  =                                                    eq. 5.4-1
                    b - a

In the case of the driving example, f(b) is your destination, f(a) is where you started from (their difference being exactly 60 miles), b is when you arrived, and a is when you started (that difference being exactly one hour). f'(x) is the speed you were driving at any time, x.

Proof of The Mean Value Theorem

Let

            f(b) - f(a)
   g(x)  =              (x - a) + f(a)                            eq. 5.4-2
               b - a

Observe that the graph of g(x) is a straight line that passes through the points, (a, f(a) ) and (b, f(b) ). Observe also that g'(x) is constant:

             f(b) - f(a)
   g'(x)  =                                                       eq. 5.4-3
                b - a

Most important, observe that

   f(a) - g(a)  =  f(b) - g(b)  =  0                              eq. 5.4-4

Clearly Rolle's Theorem applies to f(x) - g(x). That means that for some x on the interval,

   f'(x) - g'(x)  =  0                                            eq. 5.4-5

Substituting equation 5.4-3 into 5.4-5, we get

           f(b) - f(a)
   f'(x) -              =  0                                      eq. 5.4-6
              b - a

which is equivalent to equation 5.4-1.

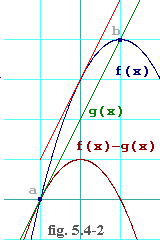
Figure 5.4-2 shows how the mean value theorem works. f(x) is shown as the blue trace. You can see that a is chosen at x = -1 and b is chosen at x = 1. The function, g(x), shown in green, is the straight line function that connects (a,f(a)) with (b,f(b)). You can see that Rolle's theorem must apply to the function, f(x) - g(x), which is shown in brown. The point where f'(x) is equal to the mean value is illustrated by the bright red tangent, which is parallel to g(x). The x where the bright red line is tangent coincides with the x where f'(x) - g'(x) = 0. That shows the connection between the mean value theorem and Rolle's theorem.

Important Consequence of the Mean Value Theorem

Suppose f(x) is a continuous function and that f'(x) is also continuous. Suppose also that you know exactly what f(x) and f'(x) are at x = a. You'd like to approximate what f(x) is at some x that is a short ways away from a, at say a+h. If you draw a line between the points, (a, f(a)) and (a+h, f(a+h)), it would have a slope of

         f(a+h) - f(a)
   m  =                                                           eq. 5.4-7a
               h

or equivalently

   f(a+h) = f(a) + hm                                             eq. 5.4-7b

The mean value theorem tells us that somewhere on the interval, a £ x £ a+h, there must be an x_mean such that

   m  =  f'(x_mean)                                                eq. 5.4-8

Not only that, but since f'(x) is continuous, the smaller h is, the closer f'(a) must be to m. This is because as h gets smaller, x_mean gets squeezed into a tighter and tighter interval (think of h as your d and |f'(a) - f'(x_mean)| as your e, and you will see that the delta-epsilon contract for continuity requires f'(a) to get as close as you like to f'(x_mean)). And the closer those two become, the more sense it makes to use f'(a) as an approximation for m = f'(x_mean). Or another way of saying this is that

   m  =  f'(a) + error                                            eq. 5.4-9

   0  =   lim  error
         h  > 0

Substitute that back into 5.4-7b and you have

   f(a+h)  =  f(a) + h(f'(a) + error)                           eq. 5.4-10

Of course, you can't know what error is, but you do know that it gets as small as you would like it to as h goes to zero. And this is why, when you are taking a limit as h goes to zero, and both f(x) and f'(x) are continuous, you can always substitute the term, f(a+h), with f(a) + hf'(a). You will recall that we have already used this fact in some of the proofs given here for the product rule and the chain rule. And we shall be using it again soon.

Exercise

Reproduce the above logic to show that when f(x) and f'(x) are continuous, and you are taking the limit as h goes to zero, you can always substitute the expression, f(a-h) with f(a) - hf'(a). I won't show you the answer here because the answer is contained in the text that precedes this exercise.

Return to Table of Contents

Move on to 5.5 Drawing a Nonblank (how to do graphing problems)

email me at hahn@netsrq.com