Solutions to Problems in 10.3
© 2000 by Karl Hahn
First use the table to find the area function (and hence
also the indefinite integral) of f(x) = x1/2.
We see that the indefinite integral is
2
F(x) = x3/2 + C
3
where C is an undetermined constant. Now remember that we use the indefinite integral
without the undetermined constant to form the bracket-expression:
|
121
 4
4
|
x1/2 dx =
|
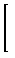
|
2
x3/2
3
|
121
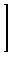 4
4
|
The bracketed expression must be evaluated at x = 121 and
at x = 4, and the answer is the difference between those two values. For
the first one I get 2662/3. And for the second one I get 16/3. The difference is
2662 - 16 2646
= = 882
3 3
which is the answer.
Return to Main Text
First use the table to find the area function (and hence
also the indefinite integral) of f(x) = 2x. We see that the indefinite integral is
1
F(x) = 2x + C
ln(2)
Notice that the - 1 in the expression in the table (which is itself
a constant) has been
absorbed here into the undetermined constant, C.
Now set up the bracket-expression using the indefinite integral (without the constant, C)
together with the limits of integration:
|
3
 0.5
0.5
|
1
2x dx =
ln(2)
|
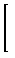
|
2x
|
3
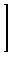 0.5
0.5
|
Observe how you can factor the constant, 1/ln(2), out of the brackets. Now simply evaluate the bracket-expression
at x = 3 and at x = 0.5, and take the difference. Since
23 = 8, and 20.5 = sqrt(2),
you get
1 _
(8 - Ö2)
ln(2)
which is the answer.
Return to Main Text
This one is a little easier than the last. Again use the table to find
the expression for the indefinite integral. In this case you come up with
1
F(x) = x3 + C
3
where C again is the undetermined constant. Now write the bracket expression in which you bracket
the indefinite integral, posting the limits of integration above and below the right-hand bracket, and dropping
the undetermined constant:
|
2
 5
5
|
x2 dx =
|
|
1
x3
3
|
2
 5
5
|
1
=
3
|
|
x3
|
2
 5
5
|
Again observe how you can factor the constant multiplier out and bring it outside of the brackets. Now just substitute each of the limits
for x and take the difference. Remember that it is the upper limit minus the lower limit. When you substitute
x = 2 into x3, you get 8. When you substitute
x = 5, you get 125. So
|
2
 5
5
|
1 117
x2 dx = [8 - 125] = -
3 3
|
which is the answer. Notice that we got a negative answer this time, or using
the idea of this being the area under the curve, we got a negative area. But
that is because we took a positive function and integrated it right
to left (the upper limit smaller than the lower limit) instead of left to
right.
Return to Main Text
This is one is also pretty easy, and you might be able to guess at what the indefinite integral is
without looking at the table. But don't be shy about looking if
you need to. You would have found that
3
F(x) = x2 + 4x + C
2
where again C is that undetermined constant. Now make the bracket equation:
|
5
 -5
-5
|
3x + 4 dx =
|
|
3
x2 + 4x
2
|
5
 -5
-5
|
Now put in x = 5 and x = -5 into the
expression inside the brackets and take the difference. I get 115/2 for the former and -35/2
for the latter. Taking the difference and simplifying the resulting fraction, I get 40, which is the answer.
Return to Main Text
Again the table will give you the indefinite integral.
1
F(x) = x2 + C
2
Making the bracket equation you get
Don't be alarmed now by having one of the limits being a symbol instead of a number. Just do with
it what you did with the limits in all the other problems in this set. Set x = b
and x = 0, and take the difference. For the former I get mb2/2,
and for the latter I get zero. So the answer is mb2/2.
Return to Main Text
email me at hahn@netsrq.com

