Karl's Calculus Tutor - Solution to Exercise 5.2-3

Box 5.2-3: Solution to Exercise 5.2-3

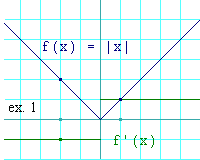
Here's a problem that has stationary points, a cusp, and endpoints. Here's the function again: f(x) = (|x-2| - 2)² + x - 5. Looks pretty nasty, doesn't it? You are probably asking yourself how you can take the derivative of thing considering it has the absolute value function right in the middle of it. The answer is to apply the chain rule just as you would to any other composite function. Abs(x) graph

For review, here again is the graph of f(x) = |x|, along with the graph of its derivative. Let's call its derivative, abs'(x). Notice again that abs'(x) is 1 for x > 0 and is -1 for x < 0. Now we are ready to apply the chain rule to the first summand of our function. We need to find the derivative of (|x-2| - 2)².

Let g(h) = h². Let h(x) = |x-2| - 2. Then g'(h) = 2h and h'(x) = abs'(x-2) . What we want to take the derivative of here is g(h(x) ). By the chain rule, we know that this derivative is:

   g'(h(x) )h'(x)  =  2h(x) h'(x)  =  2(|x-2| - 2) abs'(x-2)

So taking the entire derivative of f(x) = (|x-2| - 2)² + x - 5 is simply a matter of adding an easy term (i.e., the derivative of x - 5) to what we've done so far:

   f'(x)  =  2(|x-2| - 2) abs'(x-2)  +  1

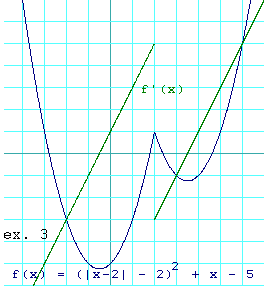Here is the graph of this f(x) and f'(x). Observe that all the nastiness of this function takes place at x = 2. Everywhere else, the behavior of this function is quite ordinary. Therefore it makes sense to break this problem up into two regions, x < 2 and x > 2, and deal with the two regions separately.

In the region of x < 2 it is true that |x-2| = 2 - x and |x-2| - 2 = -x. So in this region, it is true that f(x) = (-x)² + x - 5 = x² + x - 5. If we take the derivative in this region, we get f'(x) = 2x + 1. To find any stationary points, we solve for f'(x) = 0, and we find a stationary point at x = -0.5. Of course we need only consider it if it is in the region x < 2, and it is in that region, so it is a real stationary point. When we take the second derivative, we find that f"(x) = 2, which is always positive. So this stationary point, (-0.5, -5.25), is a local minimum.

Now for the other region, where x > 2. In this region, |x-2| = x - 2 and |x-2| - 2 = x - 4. Therefore, in this region it is true that f(x) = (x - 4)² + x - 5 = x² - 7x + 11. (Work the algebra out on paper if you are unsure where x² - 7x + 11 came from). Here, when we take the derivative, we find f'(x) = 2x - 7. Solving for f'(x) = 0, we find that we expect a stationary point at x = 3.5. This point is in the region we are examining (that is x > 2), and so it is, in fact, a stationary point for our function. When we take the second derivative in this region, we find again that f"(x) = 2, which is always positive. So this stationary point, (2, -1.25), is also a local minimum.

That takes care of the stationary points. But we know this function has a cusp as well. How do we know that? Because its derivative is discontinuous and the discontinuity passes though zero. On the graph, you can see that f'(x) goes from 5 as x approaches 2 from below to -3 as x approaches 2 from above. So indeed it does jump through zero. And as you go through the jump from left to right, it is a decreasing jump. By the rule we discussed in the first problem, this means that x = 2 must be a local maximum. It is easy to plug 2 in for x and discover that f(2) = 1. So we have a local maximum at (2, 1).

Finally we have to evaluate the endpoints, x = -4 and x = 8. Here are the evaluations at the endpoints:

         left              right
       f(-4)  =  7       f(8)  = 19
       f'(-4) = -7       f'(8) =  9

By endpoint rules we discussed in problem 1, we can see that both (-4, 7) and (8, 19) are local maximums.

Return to Main Text

email me at hahn@netsrq.com