Box 5.2-5: Solution to Exercise 5.2-5
© 1997 by Karl Hahn
Here's a problem with two a cusps and a stationary point.
Here's the function again:
f(x) = |x2 - 5x + 6|.
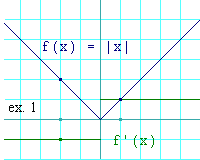
For review, here again is the graph of f(x) = |x|,
along with the graph of its derivative. Let's call its derivative,
abs'(x).
Notice again that abs'(x) is 1 for
x > 0 and is -1 for
x < 0.
Now we are ready to apply the
chain rule to the first summand of
our function. We need to find the derivative of
|x2 - 5x + 6|.
Let g(h) = |h|. Let
h(x) = x2 - 5x + 6. Then
g'(h) = abs'(h) and
h'(x) = 2x - 5.
What we want to take the derivative of here is g(h(x) ).
By the chain rule, we know that this
derivative is:
g'(h(x) )h'(x) = abs'(h(x) )h'(x) = abs'(x2 - 5x + 6)(2x - 5)
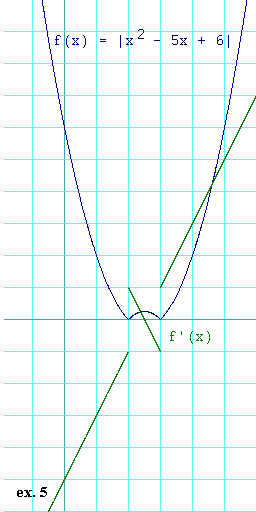Here is the graph of this f(x) and f'(x).
First observe that f(x) = |x2 - 5x + 6|
can be factored into f(x) = |(x - 2)(x - 3)|.
Now observe
that all the nastiness of this function takes place at the two
zeros of f(x), that is at
x = 2 and at x = 3.
Everywhere else, the behavior of this quite ordinary.
Since there are two nasty points this time, it breaks the
x-axis into three regions: region 1 is x < 2,
region 2 is 2 < x < 3, and region 3 is
x > 3.
In region 1, (x - 2)(x - 3) is always positive.
Why? Because both (x - 2) and
(x - 3) are negative in this region, and the
product of two negatives is always positive. That means that for
the region of x < 2, it is always true that
f(x) = |x2 - 5x + 6| = x2 - 5x + 6.
In region 2, (x - 2)(x - 3) is always negative.
Why? Because in this region, (x - 2) is positive
and (x - 3) is negative, and a positive times a
negative is always negative. That means that for the region of
2 < x < 3, it is always true that
f(x) = |x2 - 5x + 6| = -x2 + 5x - 6.
In region 3, (x - 2)(x - 3) is always positive.
Why? Because both (x - 2) and
(x - 3) are positive in this region, and the
product of two positives is always positive. That means that for
the region of x > 3, it is always true that
f(x) = |x2 - 5x + 6| = x2 - 5x + 6.
Taking the derivatives separately in each of the three regions we find that
f'(x) = 2x - 5 when x < 2.
We find also that f'(x) = 5 - 2x when
2 < x < 3.
And finally we find that f'(x) = 2x - 5 again
when x > 3.
In all three cases, f'(x) is zero at x = 2.5.
But x = 2.5 is in region 2. So that is the context
in which we must examine this stationary point. Here, we have determined that
f'(x) = 5 - 2x. So f"(x) = -2,
which is negative. By our rules, that means that x = 2.5
is a maximum.
We can also see from the graph that f(x) has two cusps. How
do we know that? Because we can see that f'(x) has two places
where it "jumps" through zero. These are at x = 2 and
at x = 3 . Such a jump is the signature of a cusp.
In this case, both jumps are increasing. By our rules that means that
both cusps are minimums.
Return to Main Text
email me at hahn@netsrq.com