Karl's Calculus Tutor - Solution to Exercise 5.2-6

Box 5.2-6: Solution to Exercise 5.2-6KCT logo

© 1997 by Karl Hahn

This problem involves finding both the first and second derivatives of 

              4x
   f(x)  =        
            1 + x2
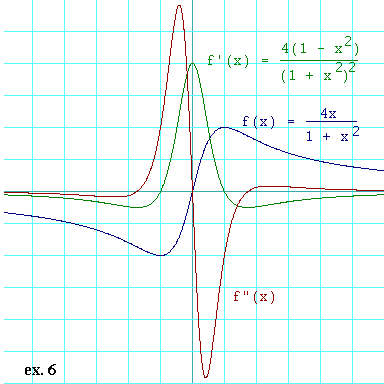
and, as stated before, you will need to use both the quotient rule and the chain rule to determine them. graph of f(x), f'(x) and f"(x)

Here is a graph of the function and its first and second derivatives. The function itself is shown in blue, the first derivative in green, and the second derivative in brown.

To find maximums and minimums we must first determine the first derivative. Because f(x) is the quotient of two polynomials, we need to use the quotient rule in order to find f'(x).

To use the quotient rule, you need to separate f(x) into a numerator function, n(x), and a denominator function, d(x). In this case, if we let  n(x) = 4x  and  d(x) = 1 + x2, then we have 

            n(x)
   f(x)  =      
            d(x)
You can quickly determine that  n'(x) = 4  and  d'(x) = 2x.

The quotient rule tells us that 

             d(x)n'(x) - n(x)d'(x)
   f'(x)  =                       
                      d2(x)
If you substitute the expressions we have for n(x), d(x), n'(x), and d'(x) into the above, you get 
             4(1 + x2) - 8x2
   f'(x)  =                 
                (1 + x2)2
And when you gather up like terms in the numerator, you get 
             4(1 - x2)
   f'(x)  =           
             (1 + x2)2
We know that, by definition, the stationary points are where  f'(x) = 0. To find the zeros of a quotient, it is sufficient to find the zeros of just the numerator (provided the denominator is continuous and not equal to zero at the same x where the numerator is equal to zero. In this case, the denominator,  1 + x2, is continuous and nonzero for all real x). So we have to solve 
   1 - x2  =  0
This happens only when  x = ± 1. And so  x = ± 1  are the only two stationary points that f(x) has, and hence the only candidates for maximums and minimums.

In order to know whether these points are maximums or minimums, we must determine f"(x). To do that, we have to take the derivative of f'(x), which again is a quotient. So again we have to apply the quotient rule. This time we have  n(x) = 4(1 - x2)  and  d(x) = (1 + x2)2.

To apply the quotient rule, we need to know both n'(x) and d'(x). You should quickly be able to determine that  n'(x) = -8x2. To find d'(x) it is helpful (though not necessary) to use the chain rule. That is because d(x) is the composite of  1 + x 2 and the square function. When you apply the chain rule to d(x), you find that  d'(x) = 2x(1 + x2). And when you now apply the quotient rule, you get 

             -(1 + x2)2(8x) - 16x(1 - x2)(1 + x2)
   f"(x)  =                                     
                         (1 + x2)4
It's starting to look nasty, eh? But go ahead and multiply out the numerator, then gather up like terms, and you get 
             8x(x4 - 2x2 - 3)
   f"(x)  =                  
                 (1 + x2)4
And we're in luck because that 4th degree polynomial (that appears as the second factor in the numerator) can be factored. Think of it as a quadratic in x2. What you get is 
             8x(1 + x2)(x2 - 3)
   f"(x)  =                    
                  (1 + x2)4
And as a reward for you're having led a clean life, lo and behold, we get a cancellation 
             8x(x2 - 3)
   f"(x)  =            
              (1 + x2)3
Now we can get back to using this to determine whether the stationary points of f(x), which we already determined happen at  x = ± 1, are maximums or minimums. You should be able to determine for yourself that  f"(-1) = 2, which is positive. By the rules we know for maximums and minimums, this means that  x = -1  is a minimum of f(x).

Likewise, you can determine that  f"(1) = -2, which is negative. And again, by the rules we know, this means that  x = 1  is a maximum of f(x).

If you glance at the graph, you will be able to see the two lobes of the blue trace do form a minimum and a maximum at  x = -1  and  x = 1  respectively.

But what about finding those inflection points? Well, we have to determine where f"(x) is zero. Again, this f"(x) is a quotient, and with quotients, it is sufficient to find where the numerator is zero (provided the denominator is continuous and not equal to zero at the same x value).

Here the numerator is  8x(x2 - 3). Clearly this is zero whenever  x = 0. It is also zero when  x2 = 3. That happens at 

         _
   x = ±Ö3

All three of these are inflection points. You cannot be absolutely sure of that unless you go to the fourth derivative and make sure that it is not zero at any of these points, but you are very unlikely to be tested on that. Also, it is clear from the graph that the slope of f"(x) is nonzero at each of those three points. And that can make you as sure as you need to be.

Return to Main Text

email me at hahn@netsrq.com