


Here again is figure 7-3, so you can look at the plots of sin(x) and cos(x) while we discuss them. And here is a table of values of sin(x) and cos(x) for some common values of x. These results can all be derived from basic geometry.
x degrees sin(x) cos(x)
|
|
I'd like you to think for a moment about the train on the circular track again. Suppose that train is at the station on Main Street and 10th Avenue East. What is different about when it backs up from when it moves forward? If it backs up 50 meters, doesn't it end up just as far east of Main Avenue as it does going forward 50 meters? Isn't the same true if it backs up any amount versus going forward by that same amount? Now recall that how far east or west of Main Avenue the train is is how we introduced cosine. So what this illustrates is a symmetry of the cosine functions: |
|
cos(-x) = cos(x) eq. 7.1b-1
In math lingo, we say that cosine is an even function. Any
f(x) that obeys the property,
Similarly, what happens differently to the train's north-south position depending upon whether it goes backward 50 meters or forward 50 meters? Well this time, there is a difference. But there is also a symmetry here as well. The train will end up just as far north of Main Street by going 50 meters forward as it would end up south of Main Street by by going 50 meters backward. And again you could substitute any other amount for 50 meters, and the same would still be true. Now recall that how far north or south of Main Street the train is is how we introduced sine. So with sine, the relationship is
sin(-x) = -sin(x) eq. 7.1b-2As you might have guessed, in math lingo we say that sine is an odd function. Any f(x) that obeys
(Food for thought:
Can you show that the only function that is simultaneously an even
function and an odd function is
Here is another property of sine and cosine that should be evident from the circular track model and the plot shown in figure 7-3. Both sine and cosine have a period of 2p. That is, wherever you are on the track, if you go 2p kilometers farther, you will end up at precisely the same place. Why? Because you will have gone full circle. And if you go 2p again, the same thing. Indeed if you go any multiple of 2p kilometers you will end up exactly where you started. And that means just as far north or south of Main Street, and just as far east or west of Main Avenue as you started. And what this means in terms of sine and cosine is that for any integer, n, it is always the case that
sin(x) = sin(x + 2np) eq. 7.1b-3a cos(x) = cos(x + 2np) eq. 7.1b-3b
We are ready now to review a whole raft of useful relationships among trig functions. If you can't memorize them, you should learn to derive them quickly. They will soon become tools you will need to do homework and exam problems.
Here again are the two that we developed in the main text:
sin2(x) + cos2(x) = 1 eq. 7.1-1
and
cos(a+b) = cos(a)cos(b) - sin(a)sin(b) eq. 7.1-6
From equation 7.1-1 you have immediately that
___________
|cos(x)| = Ö1 - sin2(x) eq. 7.1-1a
___________
|sin(x)| = Ö1 - cos2(x) eq. 7.1-1b
Now look at table 7-1. Notice that
cos(a - p/2) = cos(a)cos(-p/2) - sin(a)sin(-p/2) eq. 7.1b-3a
cos(a - p/2) = cos(a)×0 - sin(a)×(-1) eq. 7.1b-3b
cos(a - p/2) = sin(a) eq. 7.1b-3c
And because cosine is an even function, it follows as well that
cos(p/2 - a) = sin(a) eq. 7.1b-3d
Both of these are true for any real number, a.
Now substitute
cos(u) = sin(p/2 - u) eq. 7.1b-3e
Which is true for any real number, u. But suppose instead you
substituted
cos(u) = sin(u + p/2) eq. 7.1b-3f
which again is true for any real number, u.
Now lets take
cos(p/2 - a - b) = cos(p/2 - a)cos(-b) - sin(p/2 - a)sin(-b)
eq. 7.1b-4a
Now simply apply the identities we have so far:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b) eq. 7.1b-4band we have a way of finding the sine of the sum of two angles. So now we have formulae for both sine and cosine for the sum of angles, but what about differences of angles? You can use the sum formulae together with the even and odd properties to, substituting -b for b, to get:
cos(a - b) = cos(a)cos(b) + sin(a)sin(b) eq. 7.1b-5a sin(a - b) = sin(a)cos(b) - cos(a)sin(b) eq. 7.1b-5bYou can also use the sum formulae to derive expressions for sine and cosine of double-angles. Simply observe that
cos(2x) = cos(x + x) = cos2(x) - sin2(x) eq. 7.1b-6a sin(2x) = sin(x + x) = 2sin(x)cos(x) eq. 7.1b-6bYou can do a sneaky trick on equation 7.1b-6a to get a half-angle by substituting x/2 and combining it with
cos(x) + 1 = cos(x/2 + x/2) + 1 = cos2(x/2) - sin2(x/2) + 1 =
cos2(x/2) - sin2(x/2) + sin2(x/2) + cos2(x/2) eq. 7.1b-7a
When you cancel and simplify, you get
cos(x) + 1 = 2cos2(x/2) eq. 7.1b-7b
______________
Öcos(x)/2 + 1/2 = |cos(x/2)| eq. 7.1b-7c
Likewise, you can change signs and get
1 - cos(x) = 1 - cos(x/2 + x/2) = 1 - cos2(x/2) + sin2(x/2) =
sin2(x/2) + cos2(x/2) - cos2(x/2) + sin2(x/2) eq. 7.1b-8a
When you cancel and simplify, you get
1 - cos(x) = 2sin2(x/2) eq. 7.1b-8b
______________
Ö1/2 - cos(x)/2 = |sin(x/2)| eq. 7.1b-8c
Putting in x instead of x/2, you can use the above to
get formulae for sine squared and cosine squared:
sin2(x) = 1/2 - cos(2x)/2 eq. 7.1b-9a cos2(x) = 1/2 + cos(2x)/2 eq. 7.1b-9b(Observe what happens when you add the right-hand sides of those two equations)
Combining equations 7.1-6 and 7.1b-5a, you get
cos(a+b) + cos(a-b) = cos(a)cos(b) - sin(a)sin(b) +
cos(a)cos(b) + sin(a)sin(b) =
2cos(a)cos(b) eq. 7.1b-10a
If you divide out the 2, you can see that taking the product of
the cosines of two numbers is the same as taking half the cosine of their
sum plus half the cosine of their difference. Likewise
cos(a+b) - cos(a-b) = cos(a)cos(b) - sin(a)sin(b) +
-cos(a)cos(b) - sin(a)sin(b) =
-2sin(a)sin(b) eq. 7.1-10b
Again, if you divide out the -2, you can see that taking the product
of the sines of two numbers is the same as taking half the cosine of their
difference minus half the cosine of their sum. Similarly, you can
combine equations 7.1b-4b and 7.1b-5b to get
sin(a+b) + sin(a-b) = sin(a)cos(b) + cos(a)sin(b) +
sin(a)cos(b) - cos(a)sin(b) =
2sin(a)cos(b) eq. 7.1b-11a
sin(a+b) - sin(a-b) = sin(a)cos(b) + cos(a)sin(b) +
-sin(a)cos(b) + cos(a)sin(b) =
2cos(a)sin(b) eq. 7.1b-11b
Here's a cute one for you.
_ _ _
sin(x) + cos(x) = Ö2 (Ö2/2)sin(x) + (Ö2/2)cos(x) ) =
_
Ö2 ( cos(p/4)sin(x) + sin(p/4)cos(x) ) =
_
Ö2 sin(x + p/4) eq. 7.1b-12
It's also equal to
_
Ö2 cos(p/4 - x)
but I'm
sure you can prove that using the identities we have so far.
Surely you recall from trig that sine and cosine were not the only trig
functions you studied. They also introduced you to
sin(x)
tan(x) =
eq. 7.1b-13a
cos(x)
cos(x)
cot(x) = eq. 7.1b-13b
sin(x)
1
sec(x) = eq. 7.1b-13c
cos(x)
1
csc(x) = eq. 7.1b-13d
sin(x)
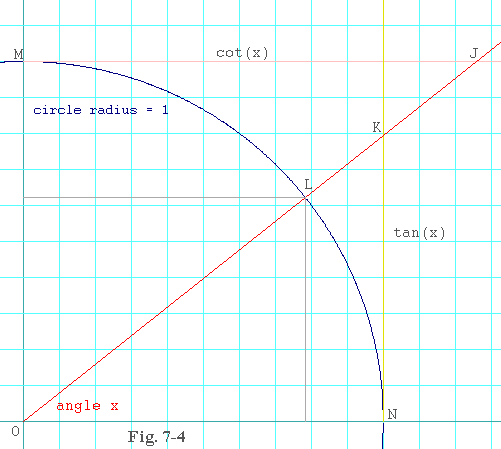
Figure 7-4 shows the geometric interpretation of these functions. Once
again, the radius of the circle is 1. The angle, x, is
still in radians. Observe that the point, L, has
coordinates of
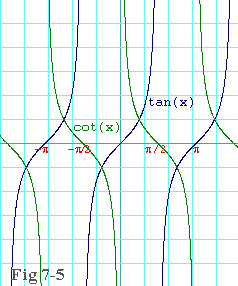
Unlike the sine and cosine, these new functions are not continuous everywhere.
For example, according to
|
Similarly,
We shall be discussing more about continuity of trig functions in a later section. |
|
|
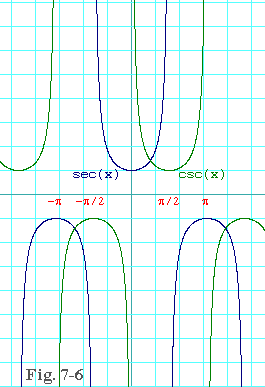
The functions, sec(x) and csc(x), follow a similar pattern. Observe in figure 7-6 that sec(x) (the blue trace) is discontinuous at odd multiples of p/2, and csc(x) (the green trace) is discontinuous at multiples of p. And the discontinuities occur for the very same reasons as they do in tan(x) and cot(x).
There are just a few identities that we'll go over concerning these
functions. First, you recall from
1
sec(x) =
so it must also be true that
1
sec2(x) =
|
|
But we all know from eq. 7.1-1 that the 1 in the numerator of
the above is the same as
sin2(x) + cos2(x)
sec2(x) = eq. 7.1b-14a
cos2(x)
With just a little algebra and a glance back at
sec2(x) = tan2(x) + 1 eq. 7.1b-14band using the identical approach you can show that
csc2(x) = cot2(x) + 1 eq. 7.1b-14c
Developing a formula for tan(a+b) is a piece of cake when you use the formulae we already have for sin(a+b) and cos(a+b).
sin(a+b)
tan(a+b) = eq. 7.1b-15a
cos(a+b)
sin(a)cos(b) + sin(b)cos(a)
tan(a+b) = eq. 7.1b-15b
cos(a)cos(b) - sin(a)sin(b)
If you divide numerator and denominator of eq. 7.1b-15b by
cos(a)cos(b), you get some cancellations.
sin(a) sin(b)
+
cos(a) cos(b)
tan(a+b) = eq. 7.1b-15c
sin(a)sin(b)
1 -
cos(a)cos(b)
Finally, applying
tan(a) + tan(b)
tan(a+b) = eq. 7.1b-15d
1 - tan(a)tan(b)
Using a very similar method you can come up one for the cotangent
(which I will let you derive for yourself):
cot(a)cot(b) - 1
cot(a+b) = eq. 7.1b-15e
cot(a) + cot(b)
email me at hahn@netsrq.com