

For an interactive view on the basics of the sine and cosine functions, see the Trig FAQ by J. David Eisenberg (requires a Java-enabled browser).
We have all heard that the earth is running out of room for all its new citizens, and how in every nation on earth the politicians have corrupted the economics to their own personal gain. And this is why the Society for New Age Future Understanding (SNAFU) was formed. At its most recent convention the delegates decided by acclaimation that SNAFU would seek to raise the undersea plateau on which once stood the proud land of Atlantis, and furthermore, that SNAFU would design and build there a utopian paradise called New Atlantis.
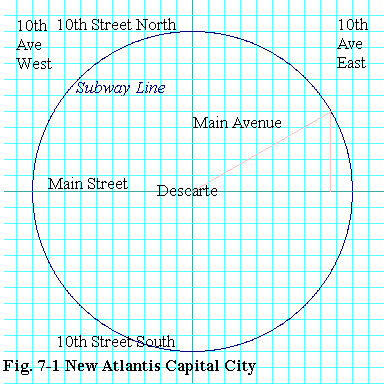
In the interest of accomplishing something toward this end while the nasty problem of raising an undersea plateau was being pondered, SNAFU gave its architectural subcommittee the job of designing the capital city of New Atlantis. They determined that at the center of town would be a great monument to Descarte. The streets and avenues would form a square grid, ten streets and ten avenues to the kilometer. Main Street and Main Avenue would intersect at the monument. Then First Street North would pass 0.1 km north of the monument, Second Street North would pass 0.2 km north of the monument, and so on. Likewise First Street South would pass 0.1 km south of the monument, Second Street South would pass 0.2 km south of the monument, and so on. The avenues would be the same except that First Avenue East would pass 0.1 km east of the monument, and so on.
But there was still the need for public transportation in the new metropolis. So the architects planned a circular subway line centered upon the monument. The radius of the circle was to be 10 blocks. So there would certainly be stations at 10th Street North and Main Avenue, at 10th Street South and Main Avenue, at Main Street and 10th Avenue East, and at Main Street and 10th Avenue West.
The subway train cruises around the track counterclockwise starting at the station at Main Street and 10th Avenue East. It travels at a steady 1 kilometer per minute. If you were riding in the train, you would be passing under the various streets and avenues. So what street and what avenue would you be under at, say, 6 seconds after the train leaves the station? How about at 12 seconds after, or one minute after? The SNAFU architects need to know these things so that they can design the automated announcement system that tells the passengers where they are.
And it is for problems like this that the world invented trigonometric functions. But as you will see, as your study of calculus continues, they will come to serve you in much broader ways. But let's begin by reviewing some basics about trig functions.
As the train moves around the circular track, you can measure the distance
it has covered along the track. You know from your previous studies,
once all the way around this track will put 2p kilometers on the
train's odometer, where
The trig functions, sin(x) and cos(x), allow us to predict how far the train is north of Main Street (in the case of sin), and how far the train is east of Main Avenue (in the case of cos), both as functions of how far the train has gone around the track. That distance along the track, starting at the station on Main Street and 10th Avenue East -- that is the x we stick into the sin and cos functions. And in this example, since the distance we put in is in kilometers, distance we get out is in kilometers as well.
But a much better way to think about it is in terms of radii of the circle. In the case of the track, the radius is 1 kilometer. In other problems you will deal with circles whose radii are something else. Hence it is useful think of the x that you stick into sin(x) or cos(x) as some number of radii of a circle. That concept is where we get the word radians, which you see used in most books on trigonometry.
So, for example, after p/6 minutes, the train has gone one twelfth of the way around the circle. This is because the train is moving at 1 kilometer per minute, and that is the same as 1 radius per minute (or 1 radian per minute, if you prefer). After p/6 minutes, it has moved p/6 radii.
If you draw a line segment from the center of the circle to where the train is after p/6 minutes, you will find that the segment forms an angle with Main Street of exactly 30 degrees. Why? Because 30 degrees is one twelfth of 360 degrees, which, as we all know, is all the way around the circle. Observe that the train is crossing 5th Street North at that moment. And it is somewhere near 9th Avenue East, heading for 8th Avenue East just then.
If you now draw a vertical line segment from where the train is Main
Street, you can see that you have a right triangle. The radial line
segment you drew is exactly 1 radius long. Call that side
of the triangle, c. Using a little
geometry (imagine the same right triangle reflected to the south of
Main Street -- the two form an equalateral triangle), you can prove
that the length of the vertical line segment is exactly 0.5
radii long. Call that side of the triangle, a.
And using the
a2 + b2 = c2 eq. 7.1-1a
_______
b = Öc2 - a2 eq. 7.1-1b
_________ _
b = Ö12 - 0.52 = Ö3/2 = 0.866025403 eq. 7.1-1c
And so we have shown that
_
cos(p/6) = Ö3/2 = 0.866025403
We have already observed that there is an angle associated with
p/6 kilometers around the track, and that in this case,
that angle is 30 degrees. And you have probably heard it
said before that "The sine of 30 degrees is 0.5."
And you have even observed that your calculator has an option for
computing sines and cosines of angles given in degrees. Right now,
go set your calculator so that it computes sines and cosines of angles given
in radians, and then leave it that way. Radians is the "natural"
measure for angles, just as e was the "natural" base
for logarithms. It is degree measure that is artificial -- invented
by ancient astronomers to make the number of degrees in a circle
approximately the number of days in a year and still have it be
evenly divisible by a lot of small whole numbers (like 2, 3, 4, 5, 6,
8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, etc.). But in calculus
texts it is almost universally understood that trigonometric functions
operate on quantities that are in radians. Things work out much tidier
that way. To convert an angle in radians to one in degrees, multiply
by
You can draw a radius line segment and a vertical line segment back to
Main Street for any position on the track that the train might ever be.
And in every case, the length of the vertical segment will be the sine
of the distance the train has gone. Of course you must observe that
when the vertical line segment extends to the south of Main Street instead
of north, the
sine is negative. Likewise the length of the horizontal side of the
triangle will be the cosine of the distance the train has gone. Again
follow the convention that if the horizontal side extends west of Main
Avenue instead of east, then the cosine is negative. And of course the
hypotenuse of the triangle is always exactly 1 radius long. So
the
sin2(x) + cos2(x) = 1 eq. 7.1-2 |
That is, the sum of the square of the sine of any number, x, with the square of the cosine of that same x is always equal to 1, no matter what x is. This formula is extremely important, so if you've forgotten it, take a minute now to remember it again. And then, don't forget it, and don't forget the reason it's true.
Also observe that the sine and cosine of any distance around the circle corresponds to ratios of the inscribed right triangle that results. Do you remember the phrases you memorized in trig? Sine is opposite over hypotenuse. Cosine is adjacent over hypotenuse. But opposite and adjacent to what? To the angle of the triangle that is at the center of the circle. And the ratios are ratios of lengths of sides of the triangle.
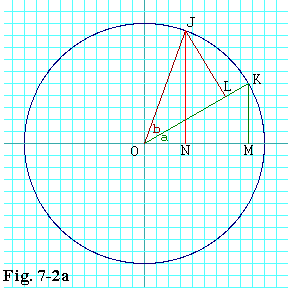
We can parley the formula from eq. 7.1-1
along with some basic geometry to get ourselves
a most useful formula for the cosine of the sum of two values. Look at
figure 7-2a. Assume the radius of the circle to be 1.
Let a be the radian measure of
And what about the lengths of the various line segments in the diagram?
To make this whole derivation easier, I'd like to appeal to your sense of symmetry. If we rotated the entire diagram clockwise about the origin by an amount equal to angle a, wouldn't all the relationships given above still be preserved? After all, the distance from Albany to Buffalo doesn't change just because the earth rotates, does it? Nor do the angles that make the Pyramids of Giza so pleasing to the eye change as the earth spins.
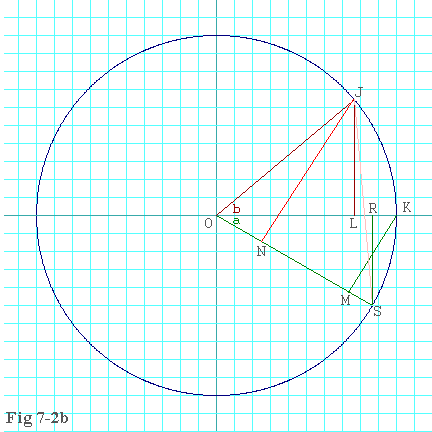
Now look at figure 7-2b. It shows the same diagram as in figure 7-2a except it's been rotated clockwise. In addition, I've added two new points, R and S, and two new line segments, RS (in green) and JS (in pink).
First observe that the length of the new line segment, RS, is the same as the length of KM, which we already determined to be sin(a). We know this because triangles ROS and KOM are congruent. From that same congruency, we know that the length of OR is cos(a).
The next thing is to determine the coordinates of points J and S as they appear in figure 7-2b. This is easy using the lengths of the line segments that we already know.
Now look at the triangle, JNS. It is a right triangle with JS as the hypotenuse. We already know the length of side JN is sin(a+b). We also know that the length of OS is 1, because that segment is a radius. We already know that the length of ON is cos(a+b). Hence
length of NS = length of OS - length of ON = 1 - cos(a+b) eq. 7.1-3The length of side JS we can get using the
_______________________
Ö(x1 - x2)2 + (y1 - y2)2
From there
_______________________________________
length of JS = Ö(cos(b) - cos(a))2 + (sin(b) + sin(a))2 =
______________________________________________________________________
Öcos2(b) - 2cos(b)cos(a) + cos2(a) + sin2(b) + 2sin(b)sin(a) + sin2(a)
eq. 7.1-4a
You should be able to see at once that we can apply equation 7.1-1 to this
last expression in two places. And that gives:
_________________________________
length of JS = Ö2 + 2sin(b)sin(a) - 2cos(b)cos(a) eq. 7.1-4b
We're getting near the end of this now. Because triangle JNS
is a right triangle, the
w2 = u2 + v2 eq. 7.1-5aAnd we have expressions for u, v, and w. So we just have to substitute them in.
2 + 2sin(a)sin(b) - 2cos(a)cos(b) = sin2(a+b) + (1 - cos(a+b))2
eq. 7.1-5b
Multiplying out the
2 + 2sin(a)sin(b) - 2cos(a)cos(b) = sin2(a+b) + 1 - 2cos(a+b) + cos2(a+b)
eq. 7.1-5c
Looks like we can apply equation 7.1-1 again:
2 + 2sin(a)sin(b) - 2cos(a)cos(b) = 2 - 2cos(a+b) eq. 7.1-5dOnce you do all the cancelling and simplifying to this, you are left with
cos(a+b) = cos(a)cos(b) - sin(a)sin(b) eq. 7.1-6 |
This equation is true for all real a and b. Again, this
identity is very important, and if you've forgotten it, it's time to remember
it once more. Equations 7.1-1 and 7.1-6 are the mother and father of all
other trig identities. You can

Figure 7-3 shows plots, which are probably familiar to you, of sin(x) and cos(x). Look at them and get a feel for where they are increasing, decreasing, where they cross the x-axis, and where they have maxes and mins. Try to relate all these features of the plots to what happens as the train goes around the circular track. These functions will be much in the news as we proceed.
You undoubtably recall learning the
a2 + b2 = c2 eq. 7.1-7
 This, of course, is a very useful rule when it comes to dealing with
right triangles. But not every triangle we encounter in life
contains a right angle. What can we say about the sides of all those
triangles that don't?
This, of course, is a very useful rule when it comes to dealing with
right triangles. But not every triangle we encounter in life
contains a right angle. What can we say about the sides of all those
triangles that don't?
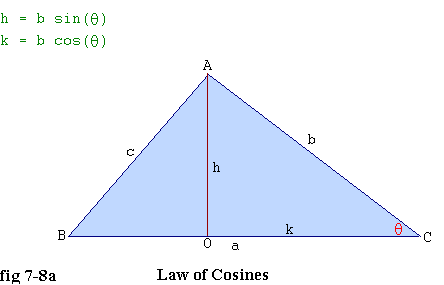
Figure 7-8a shows such a triangle. The three sides are of length a, b, and c. But the angle, q, that joins a and b is not a right angle. The red line intersects side a at right angles at the point O. The length of the red line is shown as h. That line divides the blue triangle into two right triangles, ABO and ACO. The length of the base of triangle ACO (that is the line segment, OC) is shown as k.
Our previous discussions of sines and cosines as applied to right triangles leads us to the conclusion that:
h = b sin(q) eq. 7.1-8a k = b cos(q) eq. 7.1-8bNow turn your attention to the right triangle on the left -- triangle ABO. Its sides have lengths of c, h, and
c2 = h2 + (a - k)2 eq. 7.1-9aor substituting for h and k
c2 = b2 sin2(q) + (a - b cos(q) )2 eq. 7.1-9bAnd your curiosity, by now, has led you to multiply out the square term on the right and arrive at
c2 = b2 sin2(q) + a2 - 2ab cos(q) + b2 cos2(q) eq. 7.1-9cBut you can see that we have the sum of a sine squared and a cosine squared, each multiplied by a common factor of b2. And we just finished reviewing the fact that sine squared plus cosine squared of the same angle is always equal to one. So that leaves
c2 = a2 + b2 - 2ab cos(q) eq. 7.1-9d |
This equation is called the law of cosines. It is a generalization
of the

Out of sheer laziness I've decided to use the same diagram that I used to illustrate the law of cosines to illustrate the law of sines. Observe that the angle that I have inscribed the q into is also labeled with a C. So allow that C also represents the measure of that angle. Likewise with the angles marked A and B.
We have already seen in the derivation of the law of cosines how
b sin(C) = c sin(B) eq. 7.1-10aor equivalently
sin(B) sin(C)And if you were to construct another line from B that intersects the side b at right angles, you could do the same procedure and show that=eq. 7.1-10b b c
a sin(C) = C sin(A) eq. 7.1-10cand consequently
sin(C) sin(A)By transitivity again, all three of those ratios must be equal for any triangle.=eq. 7.1-10d c a
sin(A) sin(B) sin(C) |
In other words, the ratio of the sine of each angle of a triangle to its opposite side is equal for all three angles of any triangle. This is known as the law of sines.
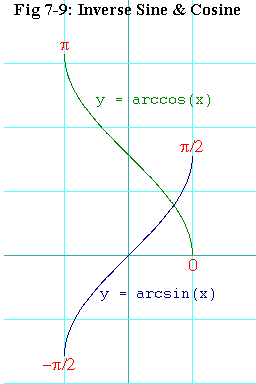
Figure 7-3 (above) shows plots of sine and cosine. Since each of these comes back to any given y-value in its range infinitely many times, you can't just transpose their graphs to form their inverses. You would end up with something that is not a function. Why? Because a function can assign no more than one range-value to each domain-value.
But inverse trig functions come up frequently in calculus, and so we
have to find a way to deal with this. And that way is simply to truncate
the range of inverse sine to
Figure 7-9 shows these two functions as I have just described them.
Observe that the domain of these functions is
You can come up with several useful identities involving arcsine and
arccosine simply by taking identities we already know about sine and
cosine and standing them on their heads. So, for example, we can
take
______
sin-1( Ö1 - x2) = cos-1(x) eq. 7.1-11
You can turn
p/2 - sin-1(x) = cos-1(x) eq. 7.1-12As an example of how you can derive such identities, I will will start with
______
Ö1 - u2 = cos(a)
______
Ö1 - v2 = cos(b)
So substituting we have
______ ______
sin(a + b) = u Ö1 - v2 + v Ö1 - u2 eq. 7.1-13a
Now take the arcsine of both sides
______ ______
a + b = sin-1(u Ö1 - v2 + v Ö1 - u2 ) eq. 7.1-13b
And since
sin-1(u) + sin-1(v) =
______ ______
sin-1(u Ö1 - v2 + v Ö1 - u2 ) eq. 7.1-13c
This is not quite right yet. The reason is because the sum,
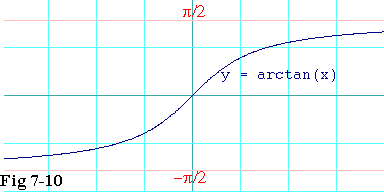
Of course if you can have inverse sine and cosine, you can have
an inverse tangent function as well. Figure 7-10 shows a plot
of it. Like sine and cosine, tangent repeats each y-value
periodically, so once again, for the purpose of forming its inverse,
we restrict the range of the inverse tangent function
to
As with arcsine and arccosine, the notation of tan-1(x) means precisely the same thing as arctan(x).
And from the identity we derived before for the tangent of a sum, we can come up with an identity for the sum of two arctangents:
arctan(a) + arctan(b) = arctan |
a + b |
eq. 7.1-14
|
You can write the arcsin and arccos functions using arctan as follows:
arcsin(x) = arctan |
x |
eq. 7.1-15a
|
||
arccos(x) = arctan |
______ Ö1 - x2 |
eq. 7.1-15b
|
Of course there are functions for arccotangent, arcsecant, and arccosecant as well, but we won't delve into them here.
And one more thing you should keep in mind about the inverse trig functions: They are useful if you know, say, the sine or cosine or tangent of an angle and need to know the angle itself. So when you find yourself in that situation, think of the word "arc."
1) We have already seen that we can come up with an identity that
equates
2) Given the equation
tan(x) = A cos(x)
where A > 0 is a constant, solve for
Move on to As The World Turns (derivatives of trig functions)