Lecture 20 - One-to-One and Onto Transformations

Learning Objectives

• Determine whether a linear transformation is one-to-one or onto
• Understand the expanded versions of the Spanning Columns Theorem and the Linearly Independent Columns Theorem

One-to-One and Onto Functions

A function \( f: U\to V \) is a rule that associates to each element \( u\in U\) a unique element \( f(u) \in V \). The element \( f(u)\in V \) is called the image of \( u \). Every element of \( U \) has exactly one image in \( V \).

We can visualize a function as a collection of arrows that point from the domain \( U \) to the codomain \( V \):

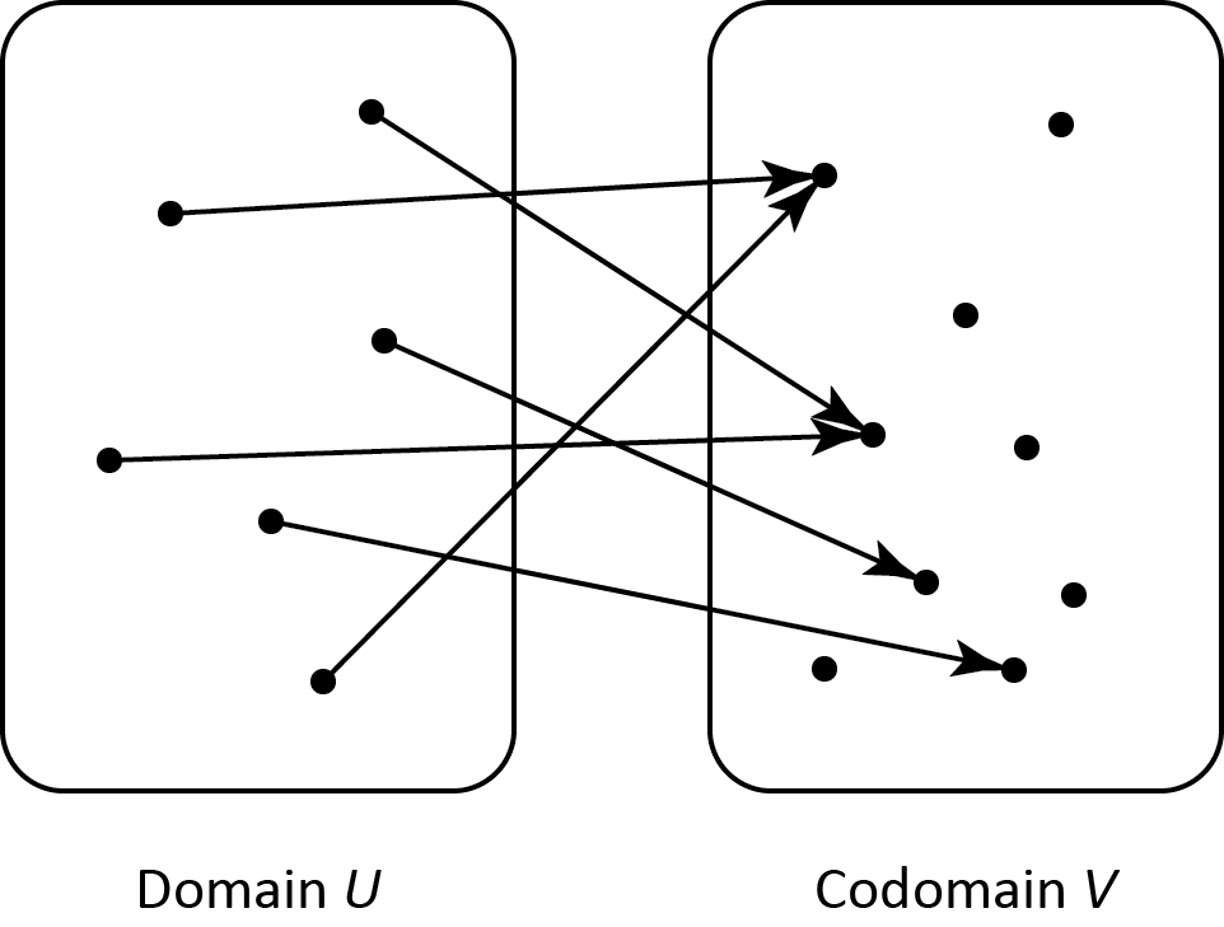
For a general function, every element of the domain has one (and only one) arrow pointing out of it. However, we can have multiple arrows that point to the same element of \( V \), and some elements of \( V \) can have no arrows pointing to them at all.

Definition. A function \( f: U\to V \) is onto (surjective) if every element of \( V \) is the image of at least one \( u\in U \).

We can visualize an "onto" function as one where every element of \( V \) has at least one arrow pointing to it:

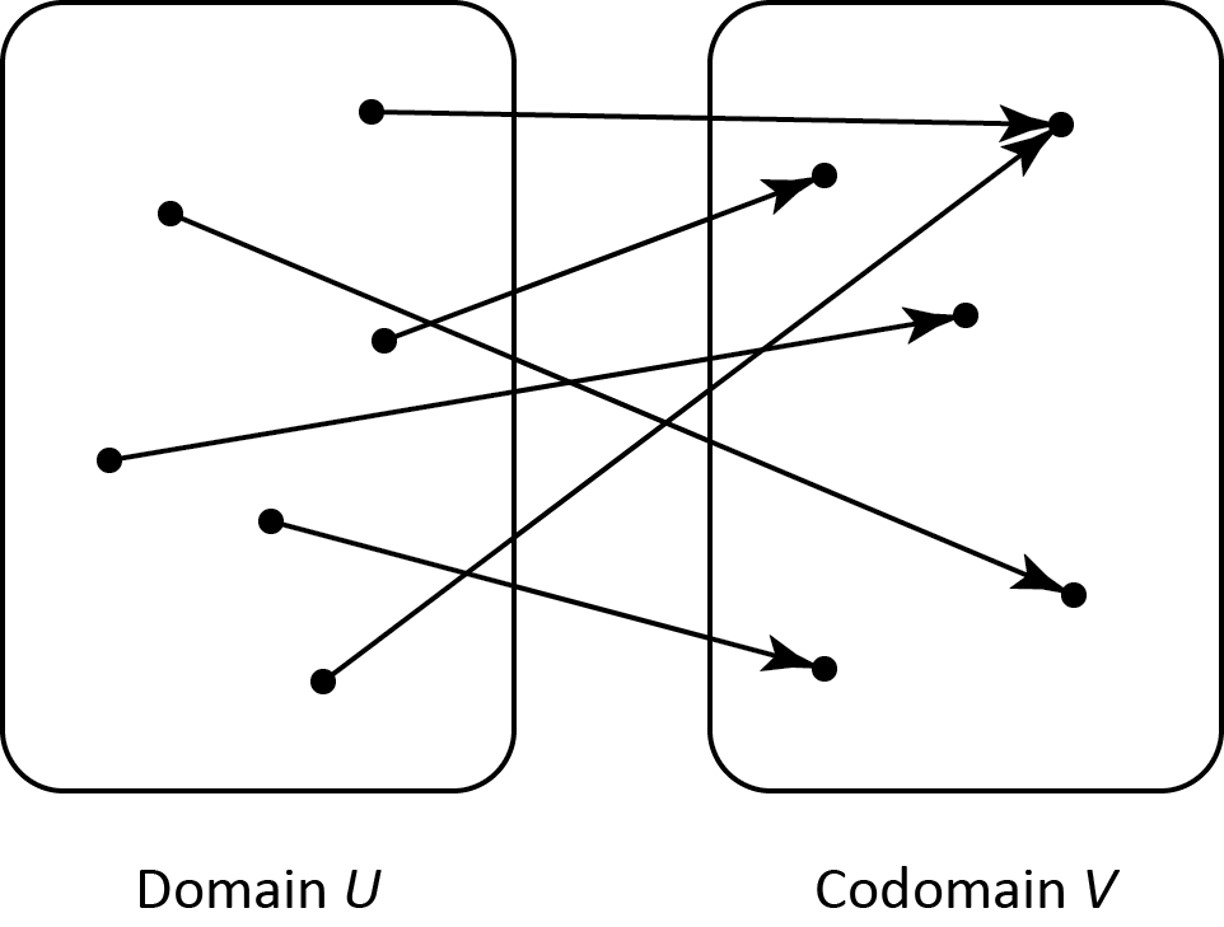
Asking "Is \( f \) onto?" is asking whether, for each \( v \in V \), the equation \( f(u)=v \) has at least one solution.

Definition. A function \( f:U\to V \) is one-to-one (injective) if everyone element of \( V \) is the image of at most one \( u \in U\).

We can visualize a "one-to-one" function as one where every element of \( V \) has at most one arrow pointing to it:

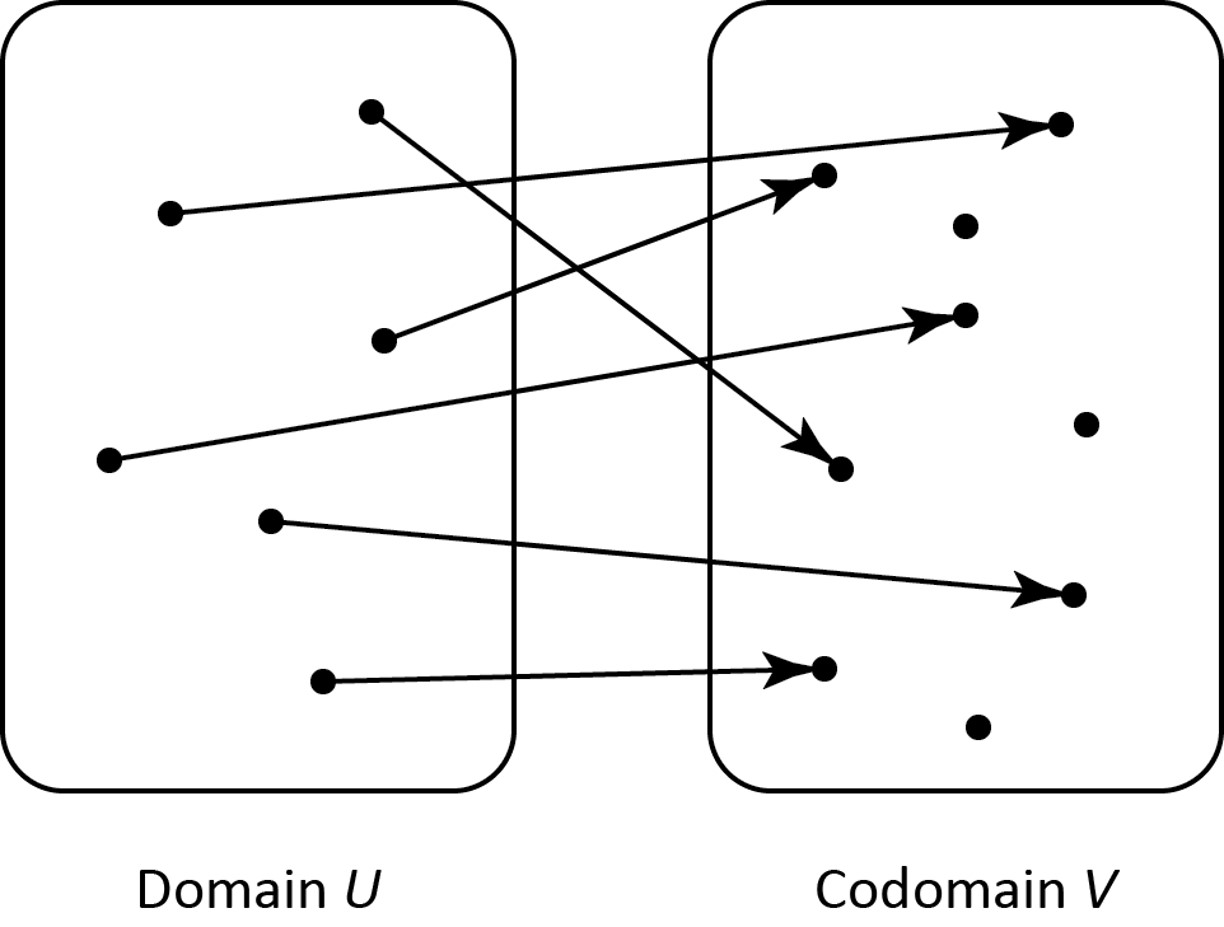
Asking "Is \( f \) one-to-one?" is asking whether, for each \( v \in V \), the equation \( f(u)=v \) has at most one solution (meaning either no solutions or exactly one solution).

One-to-One and Onto Transformations

We now want to consider what it means for a linear transformation to be one-to-one and/or onto.

Example 1A. Consider the linear transformation \( T \) whose standard matrix is \( A = \begin{bmatrix} 1 & -4 & 8 & 1 \\ 0 & 2 & -1 & 3 \\ 0 & 0 & 0 & 5 \end{bmatrix} \). Is \( T \) onto?

The question is asking us to consider the equation \( A\bbm x = \bbm b \) and whether this equation always has at least one solution. Since \( A \) has a pivot in every row, we can apply the Spanning Columns Theorem to see that, yes, \( A \bbm x = \bbm b \) is consistent for all vectors \( \bbm b \). This tells us that, yes, \( T \) is onto.

Example 1B. Consider the linear transformation \( T \) whose standard matrix is \( A = \begin{bmatrix} 1 & -4 & 8 & 1 \\ 0 & 2 & -1 & 3 \\ 0 & 0 & 0 & 5 \end{bmatrix} \). Is \( T \) one-to-one?

The question is asking us to consider the equation \( A\bbm x = \bbm b \) and whether this equation always has at most one solution. Since \( A \) does not have a pivot in every column, we can apply the Linearly Independent Columns Theorem. That theorem tells us that \( A \bbm x = \bbm 0 \) has infinitely many solutions, and so we conclude that, no, \( T \) is not one-to-one.

These examples show how the "Columns" theorems can be used to analyze a linear transformation to see whether it is onto or one-to-one. We now have "expanded" versions of these two theorems that include this analysis:

Proof of the Expanded Spanning Columns Theorem. From the definition of "onto", we know that the transformation \( T(\bbm x) = A\bbm x \) is onto if and only if the equation \( A \bbm x = \bbm b \) has a solution for all \( \bbm b \in \mathbb R^m \).

Proof of the Expanded Linearly Independent Columns Theorem. First, suppose that \( T \) is one-to-one. Then, by definition, the equation \( T(\bbm x) = \bbm 0\) has at most one solution. Since \( A\bbm 0 = \bbm 0 \), we see that \( \bbm x = \bbm 0 \) is a solution of \(T(\bbm x) = \bbm 0\). Therefore, \(\bbm x = \bbm 0 \) is the only solution.

Now, suppose \( A\bbm x = \bbm 0 \) has only the solution \( \bbm x = \bbm 0 \). Our goal is to prove that \( T \) is one-to-one, but we will assume that \( T \) is not one-to-one and try to reach a contradiction. If \( T \) is not one-to-one, then there must exist a vector \( \bbm b \) for which the equation \( T(\bbm x) = \bbm b \) has more than one solution. Let \(\bbm u_1 \) and \(\bbm u_2 \) be two different solutions of \( T(\bbm x) = \bbm b \). So \( T(\bbm u_1) = \bbm b \) and \( T(\bbm u_2) = \bbm b \). Now \( T(\bbm u_1 - \bbm u_2) = T(\bbm u_1) - T(\bbm u_2) = \bbm b - \bbm b = \bbm 0 \), so \( \bbm u_1 - \bbm u_2 \) is a solution of \( T(\bbm x) = \bbm 0 \). However, \( A \bbm x = \bbm 0 \) has only the solution \( \bbm x = \bbm 0 \), which means \( \bbm u_1 - \bbm u_2 = \bbm 0 \). But then \( \bbm u_1 = \bbm u_2 \), which is a contradiction since \(\bbm u_1 \) and \(\bbm u_2 \) are different. This contradiction shows that our assumption that \( T \) was not one-to-one was incorrect, which proves that \( T \) must be one-to-one. \( \Box \)

Example 2. Let \( T(\bbm x) = A\bbm x \), where \( A = \begin{bmatrix} -3 & 6 & 0 \\ 1 & 4 & 6 \\ 5 & -1 & 9 \end{bmatrix} \). Is \( T\) onto? Is \(T\) one-to-one?

We row-reduce the matrix and apply the "Columns" theorems: \[ \begin{bmatrix} -3 & 6 & 0 \\ 1 & 4 & 6 \\ 5 & -1 & 9 \end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 & 2 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \]

Since \( A \) does not have a pivot in every row, by the Spanning Columns Theorem, \( T \) is not onto.

Since \( A \) does not have a pivot in every column, by the Linearly Independent Columns Theorem, \( T \) is not one-to-one. \( \Box \)

Example 3. Suppose that \( A \) is a matrix with 4 rows and 3 columns. Can \(T(\bbm x) = A\bbm x\) be one-to-one? Can \(T(\bbm x)=A\bbm x\) be onto?

Since \( A\) has 4 rows and 3 columns, the maximum number of pivots \(A\) can have is 3, since each pivot must be in its own row and in its own column. Thus, \(A\) cannot have a pivot in every row, since \(A\) does not have enough columns to allow that. However, \(A\) could have a pivot in every column. We conclude that \(T\) cannot be onto, but \(T\) could be one-to-one. Note that just because \(A\) has a shape that allows it to have a pivot in every column, we don't know for sure that \(A\) actually does have a pivot in every column. We don't have enough information to conclude that \(T\) must be one-to-one, just that it could be. \( \Box \)