Section 10: Integrals

10.1 Thoughts for a Wedding Reception

You probably recall the name, Johannes Kepler, from when your high school science class covered astronomy. He was the first to figure out that the paths that the planets take around the sun are ellipses, which is Kepler’s first law of planetary motion. He came up with two other laws as well. You can learn more about Kepler by clicking here

But Kepler’s primary skill was not astronomy but mathematics. Legend has it that at Kepler’s own wedding reception he sipped his wine and pondered. But rather than pondering the nuptial joys that awaited him that very evening, he showed himself to be a true mathematician to the core. He occupied his mind with the problem of finding the volume of wine in the barrels from which his drink had been poured. He noticed the caterers periodically checking each barrel with a dipstick. If a barrel were a perfect cylinder, Kepler reasoned, then it would be easy to determine the volume of wine remaining from the mark it made on the dipstick. But barrels aren’t perfect cylinders. They are wider in the middle and narrower at the top and bottom. And in between the sides make a graceful curve that appears to be the arc of a circle. So what could possibly be the formula for the volume of such a shape, especially when it is only partially full? It was this mystery that stood that night between Johannes Kepler and marital bliss.

Since I cannot reproduce Kepler’s exact line of thinking, it is here that my tale must turn fanciful. It seems that Johannes had a second cousin named Artie, whose hobby it was to collect manhole covers from cities all over the world. Now Artie had told Johannes all about his collection at the bachelor party the night before. And he had mentioned the peculiar fact that despite covers from Vienna, London, Moscow, Constantinopal, and dozens of other cities all differing in diameter, every manhole cover from everywhere Artie had collected all had exactly the same thickness.

This got Johannes to thinking. The volume of a manhole cover is easy because it is nothing more than a short cylinder. If its thickness is h and its radius is r then its volume is given by

  V  =  pr²h                                                       eq. 10.1-1

which is the formula for the volume of a cylinder, where thickness of the manhole cover is the same as the cylinder's height.

Let's suppose that all the manhole covers are one inch thick. Here is my version of Johannes Kepler's line of thought: If he went to Artie's collection, he could pick a manhole cover that was the same radius as the base of the barrel. He could find another that was the same radius as the barrel was 1 inch above its base. And he could find another that was the same radius as the barrel was 2 inches above its base, and so on, always matching the radius of the next manhole cover to the radius of the barrel at the height where the cover is to be stacked. If he were to stack up these manhole covers in order until they were as high as the barrel, he would have a pretty good approximation of the shape of the barrel. And indeed if he were to add up the volumes of all the covers he had stacked, he would have a pretty good approximation of the volume of the barrel.

Furthermore, if he only stacked the manhole covers as high as the wine remaining in the barrel, he could add up those volumes and have a pretty good idea of the volume of wine it took to fill the barrel to that height.

But the volume of wine computed this way would not be exact. It would be off by a glass or two. Why? Because the stack of manhole covers does not exactly trace the shape of the sides of the barrel. Take the bottom manhole cover, for example. Its radius is the same as the base of the barrel. But the top of that manhole cover is already an inch high, and it still has the same radius. Yet at one inch up on the barrel, its radius is already greater than that of the bottom manhole cover. So you can see that there is some small measure of inaccuracy in computing the volume this way.

Just then one of the caterers removed an empty barrel from the table. It had left a wet ring on the butcher-paper that covered the table, and when the caterer lifted the barrel, it tore away the disk of paper inside the wet ring. Kepler watched as the caterer hauled out the barrel with the disk of paper stuck to its bottom.

If I used paper disks instead of manhole covers, he thought, I could stack them into a much more accurate approximation of the barrel. Of course it would take a lot more disks to do it that way than it would take manhole covers to do it with cousin Artie's collection. That's because paper is so much thinner than a manhole cover. But that is also why stacking paper disks, each one the same radius as the barrel is at the height it is to be stacked, is so much more accurate. Take the bottom paper disk in such a stack. Instead of having a thickness of one inch, it has thickness of about 0.003 inches. At a height of 0.003 inches, the barrel is nearly the same radius as it is at zero inches height. The barrel's radius simply can't change very much in the span of just 0.003 inches.

The principle of adding up the volumes of the disks of paper works in just the same way as stacking the manhole covers. Each paper disk is really just a very short cylinder (h = 0.003 inches), and its volume is still evaluated using equation 10.1-1. Stack enough of them up that match the barrel's radius all the way up and add up their volumes and you have a much more accurate approximation of the barrel's volume.

It's still not perfect though. The barrel's radius does change just a tiny amount in 0.003 inches, and that will lead to a tiny error in the measurement of the barrel's volume. But you can imagine that if you used thinner paper and more sheets, you could get an even more accurate approximation of the barrel's volume. Still there'd be a miniscule error. The error would be smaller than you'd get using thicker paper, but it would still exist. Indeed no matter how thin the paper you used, there would still be some error. But imagine taking the limit as the thickness of the paper goes to zero and the number of paper disks goes to infinity. The limit of that sum, if it exists, would seem intuitively to match the volume of the barrel exactly. And that limit is what integrals are all about.

We shall leave solving the wine barrel problem for a later section. Instead what we shall do now is use the same method suggested above to solve a much simpler problem -- one for which we already know the answer in advance. We know that the graph of

   f(x)  =  mx                                                     eq. 10.1-2

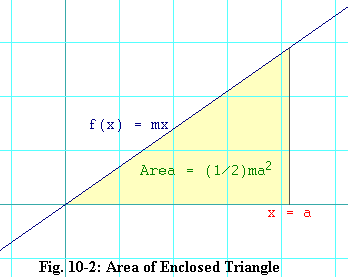is a straight line that passes through the origin. The slope of the line is given by the value of m. If you graphed this function and you drew a vertical line at x = a, then between the sloping line, the vertical line, and the x-axis, you will have enclosed a triangle. Figure 10-2 shows such a triangle. You can use the method you learned years ago to determine the area of this triangle. That is to take one half its base times its height. As shown in the figure, its base is clearly the length, a. At x = a, it is clear that f(a) = ma. So the quantity, ma, must be the triangle's height. When you take one half base times height, you get area = (1/2)ma².

What we are going to do is use the method Kepler used on the wine barrels to approximate the area of this triangle. That is, we will slice it up and approximate each slice with a rectangle. Then we will add up the areas of the rectangles to approximate the area of the triangle. Since this will only approximate the area of the triangle, we expect that the approximate area arrived at by this method will not be exactly equal to the area we got using the tried and true formula for the area of a triangle. But if we try using thinner slices and more of them, we should see the resulting approximation draw closer to the actual area of (1/2)ma². And if we take the limit as the thickness of the slices goes to zero and the number of slices goes to infinity, then it would certainly be satisfying if, in the limit, the approximation turned out to be exactly equal to the actual area.

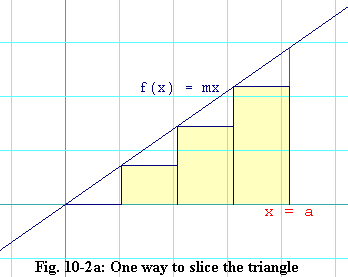
Fig 10-2a: Slicing it up into 4 Rectangles

Figure 10-2a shows one way we might slice the tringle into four slices. Each slice has a thickness of a/4. Observe that the left-hand edges of the four slices are at x = 0, x = a/4, x = 2a/4, and x = 3a/4 respectively. As promised, we have approximated each slice with a rectangle. The heights of the four slices are:

   h₁  =  f(0)     =  0

   h₂  =  f(a/4)   =  ma/4

   h₃  =  f(2a/4)  =  2ma/4

   h₄  =  f(3a/4)  =  3ma/4

That is we have used the value of the function, f(x), at the left-hand edge of each slice as the height of each rectangle. To find the area of each rectangular slice, you take its thickness, a/4, times its height. And when you add up these areas you get:

   area approximation  =  0  +  ma²/16  +  2ma²/16  +  3ma²/16

                       =  6ma²/16  =  3ma²/8                      eq. 10.1-3

We know the exact area of the triangle is ma²/2, so the approximation is short by ma²/8.

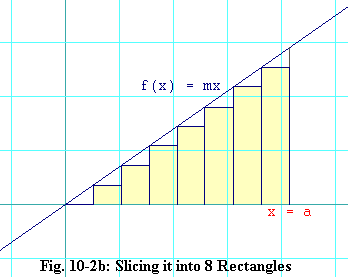
Fig 10-2b: Slicing it up into 8 Rectangles

But what if we make more slices? Let's try eight of them. You can see how this looks in figure 10-2b. Again we have used the value of the function, f(x), at the left-hand edge of each slice as the height of each rectangle. But this time the thickness of each rectangle is a/8, or half of what it was last time (since there are twice as many rectangles this time). Again we find the area of each rectangle as its thickness times its height. And the heights are:

   h₁  =  0                h₂  =  a/8

   h₃  =  2a/8             h₄  =  3a/8

   h₅  =  4a/8             h₆  =  5a/8

   h₇  =  6a/8             h₈  =  7a/8

Taking these heights times the thickness (which is the same for all of the rectangles) and summing it all up, we get:

   area approximation  =  0  +  ma²/64  +  2ma²/64  +  3ma²/64  +

                          4ma²/64  +  5ma²/64  +  6ma²/64  +  7ma²/64

                       =  28ma²/64  =  7ma²/16                    eq. 10.1-4

This time we are only short of the magic area of (1/2)ma² by ma²/16. Perhaps you are discerning a pattern here. That is, you may have already judged what the relationship is between the number of rectangular slices we use and how short the approximated area is of the actual area. But just to be sure that your judgement is right, lets take the general case of n rectangles and then take the limit as n goes to infinity.

If you divide the base of the triangle, which is length a, into n sections, then each will have length of a/n. The left-hand edge of the first section will be at x = 0a/n. The left-hand edge of the second section will be at x = a/n. The left-hand edge of the third section will be at x = 2a/n. And in general, the left-hand edge of the kth section will be at x = (k-1)/n.

That is for each integer, k, from 1 to n, we have a rectangular slice. Again we will take each rectangle's height to be f(x) where x is the left-hand edge of the rectangle (that is x = (k-1)a/n ). So in this case we get f(x) = f((k-1)/n) = h_k = (k-1)ma/n for the height of the kth rectangle. The area of that kth rectangular slice, A_k, is given by its thickness (which is a/n for every rectangle) times its height, h_k, which is:

   A_k  =  (a/n)((k-1)ma/n)  =  (k-1)ma²/n²                        eq. 10.1-5

To find the total area of the approximation, add up the A_k's for k equal 1 to n (which is another way of saying we add up the areas of all n of the rectangles). In math symbols, it looks like:

         n
   A_total  =  å A_k                                                eq. 10.1-6a
        k=1

Now substitute the expression we got for the area of the kth rectangle, A_k, in equation 10.1-5, and we get

         n
   A_total  =  å (k-1)ma²/n²                                       eq. 10.1-6b
        k=1

Notice that the factor, ma²/n², inside the summation is constant with respect to the indexing variable, k. This means we can bring it outside of the summation in accordance with the distributive law:

                 n
   A_total  =  (ma²/n²)  å k-1                                     eq. 10.1-6c
                k=1

This equation is saying simply, take the factor, ma²/n², and multiply it by the sum of the integers from zero to n-1. So how do you compute the sum of the intergers from zero to n-1? Suppose S is that sum. Then

   S  =   0   +   1   +   2   +  ...  +  n-2  +  n-2  +  n-1      eq. 10.1-7a

But because addition is commutative, you can also write that same sum backward and get the same thing:

   S  =  n-1  +  n-2  +  n-3  +  ...  +   2   +   1   +   0       eq. 10.1-7b

Now add these two equations together column by column and you get

   S  =   0   +   1   +   2   +  ...  +  n-3  +  n-2  +  n-1
   S  =  n-1  +  n-2  +  n-3  +  ...  +   2   +   1   +   0 
                                                             
  2S  =  n-1  +  n-1  +  n-1  +  ...  +  n-1  +  n-1  +  n-1      eq. 10.1-7c

On the bottom line, how many n-1's do you have? Remember that in each of the top two lines we were adding up n terms. So the bottom line should have n terms as well. And you must conclude that

  2S  =  n(n-1)                                                  eq. 10.1-7d

or equivalently

   S  =  n(n-1)/2  =  n²/2  -  n/2                               eq. 10.1-7e

We're near the end of this now. Remember that S is the sum of the integers from zero to n-1, which is also the summation in equation 10.1-6c. So we substitute that summation with the expression we got for S just above.

   A_total  =  (ma²/n²) (n²/2 - n/2)  =  ma²/2  -  ma²/(2n)         eq. 10.1-8

Perhaps you had surmised a while back that the pattern relating the number of rectangles to how good the approximation was is this: If you use n rectangles, then you will come up ma²/(2n) short of the actual area. If that was your thought then equation 10.1-8 confirms your suspicion.

Now look at what happens when you take the limit as n goes to infinity. Notice that the ma²/2 term is unaffected by the value of n. So it stays. But the ma²/(2n) term gets closer and closer to zero as n gets larger and larger. So in the limit that latter term becomes insignificant and we are left with

   A_total  =  ma²/2  =  (1/2)ma²                                  eq. 10.1-9

In other words, in the limit as you keep slicing the triangle thinner and thinner into more and more rectangular slices to approximate its area, the approximate area goes to the actual area of the triangle.

It is important that you understand this concept of slicing a shape into more and more, thinner and thinner, slices and taking the limit, as we did here. Take some time to mull it over in your mind and to review the material on this page until the concept feels comfortable to you.

Coached Exercises

1) Here's one almost the same as the one above. Let

   f(x)  =  3x + 4

We would like to find the area enclosed by the y-axis on the left, the line, x = 2, on the right, the x-axis from below, and f(x) from above. If you plot this thing you will see that it is a trapezoid whose left-hand height is 4, right-hand height is 10, and whose width is 2. So we can compute the area using the formula for the area of a trapezoid:

   A  =  (1/2)(h_left + h_right)w

   A  =  (1/2)(4 + 10) × 2  =  14

So 14 is the answer that we know ahead of time. But the way we want to do this problem is by slicing the trapezoid into n pieces, just as we did with the triangle. We will approximate each piece with a rectangle, then add up the areas of the rectangles. When we take the limit as n goes to infinity, we expect that the approximate area should go to 14.

Step 1: If you divide the width of the trapezoid into n pieces, how long will each piece be? Remember that the trapezoid's width is 2. Click here when you think you know.

Step 2: If there are n sections, and each has the length you determined in step 1, then at what x does the left-hand edge of the kth slice happen? If you have trouble with this, think about where the left-hand edge of the first one is, then where the left-hand edge of the second one is, and so on. Try to discern a pattern. When you think you have it, click here.

Step 3: The height of the kth rectangle will be f(x), where x is where the left-hand edge of the kth rectangle is. You determined that x in step 2. Now use f(x) = 3x + 4 to determine the height of the kth rectangle. Click here when you think you've got it.

Step 4: The widths of all the rectangles are the same. You found that width back in step 1. In step 3, you found the height of the kth rectangle. So what is the area of the kth rectangle? Click here when you've worked it out.

Step 5: Now write the summation expression for the sum of the areas of the rectangles. Use sigma notation for this. When you've written your sigma-expression, click here to check it.

Step 6: Note that the expression in the summation is itself the sum of two things. So write them as separate sums. That is use the sigma notation to write it as the sum over k of the first expression plus the sum over k of the second expression. Doing this will make the final steps easier. Click here when you've got it.

Step 7: From each sigma expression, factor out the stuff that is constant with respect to your index variable, k. Those factors should each come out to the left of the sigma-expression they are extracted from. Take a crack at it, and then click here to see if you did it right.

Step 8: Now take the sums of each of the sigma expressions. The first one is identical to the one we did back in equation 10.1-7a. The second one is especially easy. It's just asking you to take the sum of 1 added to itself n times. Click here when you think you've got it.

Step 9: Take the limit of the result you got in step 8 as n goes to infinity. This should be easy for you. But just in case you get confused, you can click here to see how it's done.

2) In the last two examples, the one in the text and the step-by-step coached one, you might be saying, "Big deal. I've just learned how to take the area of a triangle or trapezoid the hard way. Why not just use the formulas and do it the easy way?" Indeed as a practical matter, you should use the formulas when you encounter having to find the area of a triangle or trapezoid. But what do you do when you encounter having to find the area of a shape that has a curvy edge?

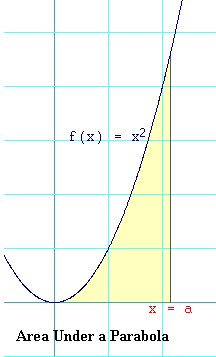
The figure to the right shows a shaded area that is bounded by the function, f(x) = x², from above, the x-axis from below, the vertical line, x = a, on the right, and the y-axis on the left. There is no convenient formula for finding this area. So in the coached exercise that follows, we shall be using the slice-it-and-take-the-limit method to find this area.

Remember that in both the triangle and the trapezoid problems you had, at one point, to find a way of summing the integers from zero to n-1. As you will see, it will turn out that in this one you will have to have a way of summing the squares of the integers from zero to n-1. Without going into the details of how to derive this formula, here it is for your reference later in the problem:

   n-1        n             n(n-1)(2n-1)
    å k²  =   å (k-1)²  =             
   k=0       k=1                 6

If you are interested in knowing a way to derive this, click here, but it is optional material and is not especially important to where we will eventually go with this slicing concept.

Step 1: If you slice the shaded area into n vertical slices, what is the width of each slice? Remember that the width of the base of this shape is a. When you get it, click here.

Step 2: If there are n slices, and each has the width you determined in step 1, then at what x does the left-hand edge of the kth slice happen? Proceed with this the same way you did in the first problem. Where does the first slice begin? Where does the second begin? And the third? See the pattern? When you do, write it down and then click here.

Step 3: Plug the result from step 2 into f(x) to find the height of the kth rectangle. When you've done it, click here.

Step 4: Determine the area of the kth slice. You know the width and you know the height. Just put them together, and then click here.

Step 5: Write the summation expression for the sum of the areas of the rectangles. Do this the same way you did with the first problem. The only difference is that you have a new expression (that you got from step 4) to put in the summation. When you're done, click here.

Step 6: Factor out that stuff that is constant with respect to k. Move that stuff to the left of the summation sign. Then check it by clicking here.

Step 7: Use the formula given to add up the sum. Do you see that your summation expression is the same as something in the formula? Just substitute. Then click here.

Step 8: Multiply it out. This is just an algebra exercise. When you're done, click here.

Step 9: Take the limit as n goes to infinity. Any term with no n in it stays. See if you can figure out what happens to the other terms. Then click here.

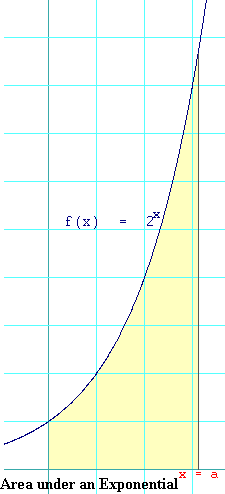
3) Just one more of these slice-and-take-the-limit problems before we move on to discuss an insight that makes finding the area under the curve a lot easier. The figure shows the function, f(x) = 2^x. Again we will find the area bounded by f(x) on top, the x-axis on the bottom, the y-axis to the left, and the line, x = a to the right. And again we know of no way to compute this area except by slicing it into rectangles, adding up their areas, and then taking the limit as the number of rectangles goes to infinity.

As in the past examples, you will reach a point where you will have to take the sum of an expression. In this case you will have to find

         n
   S  =  å u^k-1
        k=1

where u is some positive real constant. Perhaps they showed you how to do this back when you took algebra. A formula for this sum is especially useful in compound interest problems, so you might have learned it in that context. Here is how you do it. First multiply both sides by u - 1.

                        n     
   (u - 1)S  =  (u - 1) å u^k-1
                       k=1

Since u - 1 is constant with respect to the index variable, k, you can move it into the summation. This is according to the distributive law.

                 n
   (u - 1)S  =   å (u - 1) u^k-1
                k=1

Now multiply the u^k-1 through

                 n
   (u - 1)S  =   å u^k - u^k-1
                k=1

Think about what the right-hand side of this equation means. For k = 1 you have u¹ - u⁰ . For k = 2 you have u² - u¹. Notice that the -u¹ in this one cancels the u¹ in the last one. For k = 3 you have u³ - u². This time the -u² from this one cancels the u² from the last one. Indeed as you add them up one by one you can see that each of the u^k's cancels with a neighboring term except the -u⁰ in the first term and the uⁿ in the last term. Think about it.

Since u⁰ = 1, what you are left with on the right is

   (u - 1)S  =  uⁿ - 1

And we solve for the sum, S, by dividing out the u - 1.

         uⁿ - 1      n
   S  =          =   å u^k-1
         u - 1      k=1

So now you are ready to attack the problem of finding the area under the f(x) = 2^x curve. And when you reach the point where you see a sum of powers of a constant, you can refer to the above to resolve it.

Step 1: Same as last time. What is the width of each slice? You have n slices and you can see the total width of the area you are slicing. You figure it out, then click here.

Step 2: At what x is the left-hand edge of the kth rectangle? Again if you have trouble with this, figure out where the left-hand edge of the first one is, then the second, and so on. Then try to discern the pattern. When you've got it, click here.

Step 3: What is the height of the kth rectangle? Remember that the height of each rectangle is f(x), where x is where the left-hand edge of that rectangle is. Click here when you are ready.

Step 4: What is the area of the kth rectangle? Just multiply the base (which you got in step 1) by the height (which you got in step 3). Then click here.

Step 5: Write the summation formula for the sum of the areas of all the rectangles. When you've got it, click here.

Step 6: Is there any factor in the summation that constant with respect to the index variable, k? If so, factor it to the outside of the summation. Then click here.

Step 7: What exponential identity will serve you well when applied to the exponential function that remains in the summation? Observe that the exponent is the product of two things. One of them is constant with respect to the index variable, k, and the other is not. Is there a way of separating these two expressions in a way that will simplify things? I know this step is tricky, but try to tough it out. Then click here.

Step 8: Apply the summation formula for exponentials to what you got in step 7. It's easier if you keep the substituted variable suggested in the step 7 solution for now. When you've got it, click here.

Step 9: Take the limit as n goes to infinity. Hint: You have the recurring expression, a/n, in this limit. Try substituting h = a/n. Notice that as n goes to infinity, h will have to go to zero. See if you can see a familiar limit hiding in the resulting equation. When you are ready, click here.

Riemann Sums

The sums we have been taking, where we slice an area under a curve into rectangular slices and sum them up -- these are called Riemann Sums. Click here to learn more about Georg Friedrich Bernhard Riemann. Riemann was not the first to think up this kind of sum; Kepler might have been the first, and it is even possible that some of the ancient Greek mathematicians had thought along these lines. But Riemann was the first to show that if you use a continuous function to bound the area you are interested in, then when you take the limit as the number of slices goes to infinity, the limit will always exist, and it will be equal to the area that you have bounded.

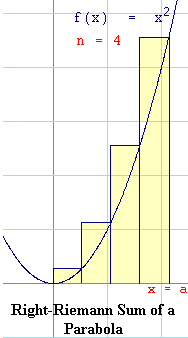
You probably noticed that in every example above, we always used the left-hand edge of each rectangle to define its height. It turns out that you can use the right-hand edge and get the exact same result when you take the limit. The two types of sums are called left Riemann sum and right Riemann sum respectively. The figure shows a right Riemann sum of f(x) = x². This is the same function we found the area under in the second coached exercise. Notice that when we took the left Rieman sum of this function, the total area enclosed by the rectangles was less than the total area under the curve. But here when we take the right Riemann sum, we find that the total area enclosed by the rectangles is more than the total area under the curve. As we take the limit, we expect that the left Riemann sum will approach the actual area under the curve from below and the right Riemann sum from above.

But notice that f(x) is an increasing function where we took the sum. If it had been a decreasing function, then it would have been vice-versa. The left Riemann sum would have been the one in excess of the area under the curve and the right Riemann sum would have been the one that was deficient. Try to visualize it to see why.

Let's set up the right Riemann sum of f(x) = x² as it is shown in the diagram. The width of each rectangle is still a/n. The height of the kth rectangle is slightly different now. Notice that the right-hand edge of the first rectangle is at x = a/n whereas the left-hand edge that we used before was at zero. The right-hand edge of the second rectangle is at x = 2a/n. The right-hand edge of the third rectangle is at x = 3a/n. And in general, the right-hand edge of the kth rectangle is at x = ka/n. So the height of the kth rectangle will be

   h_k  =  (ka/n)²  =  k²a²/n²                                    eq. 10.1-10

The area, A_k, of the kth rectangle will be its base times its height:

   A_k  =  (a/n)h_k  =  (a/n)k²a²/n²  =  k²a³/n³                   eq. 10.1-11

Summing these A_k's gives:

          n                  n
   A_total  =   å k²a³/n³  =  (a³/n³)  å k²                       eq. 10.1-12
         k=1                k=1

I will end this section by telling you that

    n        n(2n+1)(n+1)
    å k²  =              
   k=1             6

and let you prove for yourself that in this case, you get the same thing for the limit of this right Riemann sum as you got for the limit of the left Riemann sum. And remember that Riemann demonstrated that you get the same limit whether you use the left or right sum in every case.

Food for Thought

We have looked at the cases where you take the height of the rectangle by taking f(x) of the left-hand edge and at the right-hand edge. I have assured you (and later you will see proof) that in the limit, these two sums end up the same. What do you suppose would happen if you took the height of the rectangle as f(x) halfway between the left and right edges? or anywhere else in between? Remember that f(x) is assumed to be continuous. How does f(x) at an in between point compare to f(x) at either edge as the rectangles get narrower and narrower? So will you still end up with the same sum in the limit? (By the way, when you use f(x) at the halfway point between left and right edges, that sum is called the center Riemann sum)

How about if you used the mean of f(x) of the left-hand edge and f(x) of the right-hand edge? Do you think you would still end up with the same sum in the limit?

Section 10.2: Living Backward -- The Fundamental Theorem of Calculus

Return to Table of Contents

hahn@netsrq.com