Intermediate Answers to Exercise 10.1-2

The base is length a, so if you divide it into n equal slices, each slice will be a/n wide.

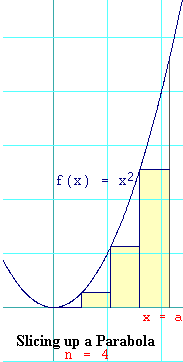
The figure on the right will help you visualize how we are slicing the area under the parabola. Here we are cutting it into four slices -- that is n = 4 (note that the leftmost slice has height of zero). The first slice has its left-hand edge at x = 0. The second at x = a/n. The third at x = 2a/n. That pattern continues. So the left-hand edge of the kth slice is at x = (k-1)a/n.

Return to main text

Recall that f(x) = x². And the result from step 2 is that the left-hand edge of the kth rectangle is at x = (k-1)a/n. So just substitute the x into the f(x) with that expression to get the height of the kth rectangle, h_k:

   h_k  =  f((k-1)a/n)  =  (k-1)²a²/n²

Return to main text

The width of every slice is a/n. The height of the kth slice is (k-1)²a²/n². So the area, A_k, of the kth slice is width times height, which is:

   A_k  =  (k-1)²a³/n³

Return to main text

Just put the expression you got in step 4 into a summation for k equal 1 to n.

          n         n
   A_total  =   å A_k  =   å (k-1)²a³/n³
         k=1       k=1

Return to main text

The factor that is constant with respect to k is a³/n³. When you factor it out you get

               n
   A_total  =  (a³/n³) å (k-1)²
              k=1

Return to main text

The summation from step 6 is just the sum of the squares of the integers from zero to n-1. We have a formula for that. When you apply it you get

               n(n-1)(2n-1)
   A_total  =  (a³/n³)             
                    6

Return to main text

When you multiply out the polynomial you get

               2n³ - 3n² + n
   A_total  =  (a³/n³)              
                    6

Now multiply through by the a³/n³:

         a³      a³      a³
   A_total  =      -       +     
          3      2n     6n²

Return to main text

The terms with n in them all have the n in the denominator. So as n gets very big, these terms become closer and closer to zero, hence they become insignificant. All that remains is the term with no n in it. So in the limit you have

   A_total  =  a³/3

which is the actual area of the shaded region that we started with.

Return to main text

How to find the sum of the squares of the integers from zero to n-1: First observe what the difference of two consecutive cubes is:

   n³ - (n - 1)³   =  n³  -  (n³ - 3n² + 3n - 1)  =  3n² - 3n + 1

Notice that we had to apply the binomial formula to unravel that.

Now observe that

   n³  =  (1³ - 0³) + (2³ - 1³) + (3³ - 2³) +  ...  

            ... + ((n-1)³ - (n-2)³) + (n³ - (n-1)³)

which works simply because everything cancels except the n³. But isn't that just the same as saying

         n
   n³  =  å k³ - (k-1)³
        k=1

Now, turning the equation around and substituting the difference expression we got using the binomial formula, we have:

    n
    å 3k² - 3k + 1  =  n³
   k=1

Try this with a few small values of n to convince yourself that it works.

The expression in the summation is itself a sum of three things. So we separate it into three summations:

    n         n         n
    å 3k²  -  å 3k  +  å 1  =  n³
   k=1       k=1       k=1

Now factor the constant multipliers from each summation:

     n          n        n
   3 å k²  -  3 å k  +  å 1  =  n³
    k=1        k=1      k=1

Starting with the easiest summation, the sum from 1 to n of 1 added to itself is pretty easy. That's equal to n.

The sum the integers from 1 to n we can do the same we we did in the main text for adding integers from zero to n-1 (by writing the sum forward and backward):

   S  =   1   +   2   +   3   +  ...  +  n-2  +  n-1  +   n
   S  =   n   +  n-1  +  n-2  +  ...  +   3   +   3   +   1
                                                            
  2S  =  n+1  +  n+1  +  n+1  +  ...  +  n+1  +  n+1  +  n+1

Clearly twice the sum is n+1 added to itself n times. So

    n       n(n+1)
    å k  =        
   k=1        2

So substituting for the two sums that we know, our equation becomes:

     n         n(n+1)   
   3 å k²  -  3         +  n  =  n³
    k=1          2

Now move all the stuff that we have resolved so far over to the right and divide by 3

    n        n³     n(n+1)     n
    å k²  =     +          -   
   k=1        3       2       3

This gives the sum of the square integers from 1 to n. But we wanted the sum from zero to n-1. So we have to add zero squared and subtract n². Of course zero squared is zero, so we ignore that. Here is the result:

   n-1       n³     n(n+1)     n
    å k²  =     +          -     -  n²
   k=0        3       2       3

Now multiply out the n(n+1), and put everything over a common denominator:

   n-1     2n³ + 3n² + 3n - 2n - 6n²     2n³ - 3n² + n     n(2n² - 3n + 1)
    å k²  =                           =               =                 
   k=0                  6                      6                  6

All that remains for you to do to finish this is to factor the quadratic on the right.

Return to Main Text

email me at hahn@netsrq.com