Intermediate Answers to Exercise 10.1-3

Along the x axis, the area you are interested goes from x = 0 to x = a. So the total width is a. When you divide it up into n slices, you get n/a.

Return to main text

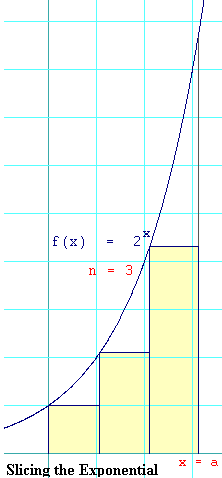
The diagram shows the area under the exponential sliced into three rectangles ( n = 3 ). The left-hand edge of the first rectangle is at x = 0. The left-hand edge of the second rectangle is at x = a/n. The left-hand edge of the third rectangle is at x = 2a/n. The pattern appears to be that the left-hand edge of the kth rectangle is at x = (k-1)a/n.

Return to main text

Since you know that f(x) = 2^x, and that the x for the left-hand edge of the kth rectangle is at x = (k-1)a/n, you can determine that the height, h_k, of the kth rectangle is

   h_k  =  f( (k-1)a/n )  =  2^(k-1)a/n

Return to main text

Area is the base times the height. You determined that the base of every rectangle is a/n. And you determined that the height of the kth rectangle is h_k = 2^(k-1)a/n. So the area, A_k of the kth rectangle is

   A_k  =  (a/n) 2^(k-1)a/n

Return to main text

You are going to have the summation of the rectangles' areas:

    ^{n
   A_total  =   å A_k
         k=1}

Now you have to substitute A_k with the expression for it that you got in the previous step.

          n
   A_total  =   å (a/n) 2^(k-1)a/n
         k=1

Return to main text

Clearly the a/n that is in multiplied by the exponential function is constant with respect to k. So we factor that out.

                n
   A_total  =  (a/n)  å 2^(k-1)a/n
               k=1

Return to main text

Do you remember from algebra that

   b^pq  =  (b^p)^q  =  (b^q)^p

This is the identity you need to use here. Your exponent is the product of (k-1) and a/n. So we apply that to our equation. But there are two ways of doing it. Here are both:

                n                n
   A_total  =  (a/n)  å (2^a/n)^(k-1)  =  (a/n) å (2^(k-1))^a/n
               k=1              k-1

So which one to use? Well the first has the expression, (2^a/n), raised to the (k-1) power. The significance here is that (2^a/n), is constant with respect to the index variable, k. So if you substituted

   u  =  2^a/n

You would have

                n
   A_total  =  (a/n)  å u^k-1
               k=1

Look familiar? You can apply the summation formula given at the beginning of the problem to this.

Return to main text

The summation formula tells you that

    n       uⁿ - 1
    å u^k-1  =        
   k=1      u - 1

Stick that in for the summation in what we already have and you get

               uⁿ - 1
   A_total  =  (a/n)       
               u - 1

When you substitute back the 2^a/n = u, you get

               (2^a/n)ⁿ - 1
   A_total  =  (a/n)            
                 2^a/n - 1

But now you can use that exponential identity again. Remember? It means that (2^a/n)ⁿ = 2^n(a/n) = 2^a. So your final equation from this step is

                2^a - 1
   A_total  =  (a/n)         
               2^a/n - 1

Return to main text

When you make the suggested substitution, you get

            2^a - 1
   A_total  =  h        
            2^h - 1

You now have the limit of this as h goes to zero. But rearrange this thing just a little, and you have

            h
   A_total  =         (2^a - 1)
         2^h - 1

Do you remember from Exponentials and Logarithms what the limit definition of natural log is?

           b^h - 1
    lim            =  ln(b)
   h  > 0     h

So when you take the limit as h goes to zero of

      h
         
   2^h - 1

you're going to get 1/ln(2). So the final result is

         2^a - 1
   A_total  =        
          ln(2)

Return to main text

email me at hahn@netsrq.com