Section 5: Applications of DerivativesKCT logo

© 1997 by Karl Hahn

5.3 The Way to Shangrila

When somebody asks you to find x in, for example, 

   x2 - 7x + 11  =  0                                             eq. 5.3-1
you, undoubtably recall from algebra, that there is a formula for problems like these. The quadratic formula says, in this case, that 
              _________          _
         7 ± Ö72 - 4×11     7 ± Ö5
   x  =                  =                                        eq. 5.3-2
               2               2
and in this way you can find the zeros of x2 - 7x + 11 or of any second degree polynomial that has real values of x that cause it to be zero. Once you've memorized the quadratic formula, problems like these are no-brainers.

But what if somebody asked you to find the x that solves 

   x3 + 16x2 - 52x - 15  =  0                                     eq. 5.3-3
Not as easy, eh? But for cubics (that is third degree polynomials), there is also a formula (and oddly enough it is called the cubic formula) that tells you what x values make them zero. If you bothered to click and see the cubic formula, you have, with near certainty, determined it to be nasty.

For fourth degree polynomials (that is quartics), there is also a formula to find the zeros. And that formula is a whole lot nastier than the cubic formula. If you want to see where that one comes from, click here, but remember that it is optional material and won't be on your exam.

When you get to fifth degree polynomials (that is quintics) and higher degree than that, you get to the ultimate in nastiness. And that is that there simply is no formula that gives you their zeros in terms of roots and powers. I don't mean just that no formula has been discovered. Mathematicians have proved that no such formulas exist, so it is pointless even to go looking for them.

But quadratics are not all peaches and cream either. When you are trying to find the solution to a quadratic using the quadratic formula, you still have to take the square root of something. Granted that if you have an electronic calculator with a square root key, taking a square root is no more difficult than multiplying or adding. Yet multiplying and adding are operations we learned to do in grammar school using pencil and paper. Finding a square root can be done with pencil and paper too, but only with much more trouble. So what is a good way to find a square root, and why is it good? We shall get back to that shortly. But first, a little story.

Long ago an order of wise monks founded the hamlet of Shangrila. At first, they were unable to attract settlers into their little paradise-on-earth. You see, Shangrila is isolated far from nearest village or farm. It is hidden in a valley that you cannot see until you are right upon it. The way to the valley is long and tortuous, with many opportunities to lose you way and perish in the wind-blown snows of the Himalayan peaks.

So the monks set upon a project of erecting stone signposts all through the wilderness to direct travelers unerringly to Shangrila. And their efforts were successful -- in fact too successful. Soon there was a steady stream of settlers arriving in Shangrila, and their numbers soon became a burden to the public parks, schools, and sewers. So the monks set off into the wilderness once again to tear down the signposts they had erected only a few decades earlier. Unfortunately, they had grown older and physically weaker in that time. Tearing down the stacks of stones was too much exertion. So instead they redirected the pointers. They started at the signposts that were farthest way from Shangrila, and those they nudged quite a bit, until they were pointing somewhere other than at Shangrila. Then gradually they worked toward the signposts that were nearer and nearer to Shangrila. But winter was fast approaching, and the closer they got to Shangrila, the faster they had to work. Consequently, the signposts closest to Shangrila were the ones they nudged the least.

So the intrepid traveler can still find his or her way to Shangrila, but it is never along a direct route. You have to wander around the wilderness until you find one of the ancient signposts. You follow the direction and distance it instructs, even though that information is not entirely accurate. Then once having gone that distance and direction, you must wander until you find another signpost. Its information will not be entirely accurate either, but because you are now closer to Shangrila than when you started, the information on this signpost is somewhat more accurate than what you found on the last one. So now, follow the new instructions, then wander until you find yet another signpost. If you keep this up long enough, it will bring you within sight of Shangrila.

Shangrila, the Place Where f(x) = 0

If you have a first degree polynomial, that is 

   f(x) = ax + b                                                  eq. 5.3-4

and you want to find where f(x) = 0, what you find is that the derivative, f'(x) = a, points right at the solution. What do I mean by that? Pick an a and a b. Sketch a graph of the resulting f(x). I'll pick a = 3 and b = 1. Now pick any value for x. Just pick one at random. I'll pick x = 10. We have f(10) = 10a + b = 31. So the point, (10, 31) is on the my graph.

If I then walk from (10, 31) toward the x axis, but for every unit I walk in the y direction, I walk 1/a = 1/3 units in the x direction, I find that by the time I get to the x axis, I have gone 31/3 units to the left in the x direction. I will have arrived at the point, (10 - 31/3, 31 - 31) = (-1/3, 0). All I have done here is walk in the exact direction that the function points me until I got to the x axis. And what x value did I arrive at? I arrived at x = -1/3. And now see what you get if you put -1/3 in for x into 5.3-4. You got f(-1/3) = 0, didn't you? The signpost points directly to Shangrila in this case.

So what did we do to find Shangrila (which, by metaphorical definition, is where f(x) = 0)? We picked an arbitrary value of x (in this case x = 10). Let's call the arbitrary x that we picked x0. Using x0 as a starting point, we found a new x, which we'll call x1 by taking

Figure 5.3-1 
   f(x0)  =  3x0 + 1                                              eq. 5.3-5a
and 
   f'(x0) = 3                                                     eq. 5.3-5b
Then we subtracted the quotient of these two values from x0, and that is what we took to be x1. It turned out that x1 landed us right at Shangrila's village temple.

In the case of f(x) being a 1st degree polynomial such as we have here, it doesn't matter what you choose for x0. If you use the procedure above on x0 to generate x1, then x1 will always place you right at Shangrila. That's because with a 1st degree polynomial, the monks haven't messed with the signposts yet. They all point directly to Shangrila. To follow a signpost at x0 (no matter where that happens to be), all you do is 

               f(x0)
   x1  =  x0 -                                                    eq. 5.3-6
               f'(x0)
and you have the key to the temple.

By using just a little algebra, we can readily see why it doesn't matter what you choose for x0 (that is for 1st degree polynomials). If f(x) = ax + b and f'(x) = a, then 5.3-6 becomes 

               ax0 + b          ax0   b               b
   x1  =  x0 -          =  x0 -     -    =  x0 - x0 -             eq. 5.3-7
                  a              a    a               a
So you can see that x0 cancels completely, and that x1 = -b/a no matter what x0 is. If you substitute -b/a in for x into f(x) = ax + b, you'll find that it always gives you zero (try it). And where f(x) = 0 is Shangrila in our math-world.

Earlier I promised I'd show you a way to find square roots. We do this by constructing a polynomial whose zero is the square root of one of its coefficients. The polynomial that does that is 

   f(x)  =  x2 - C                                                eq. 5.3-8
You will agree, won't you, that when you substitute x = ±sqrt(C) into 5.3-8, you will always get zero. All we have to do is find the x that makes this f(x) become zero. Are you ready to travel to Shangrila?

We are going to use the same method for finding Shangrila this time as we did in the case of the 1st degree polynomial. Let's say that we want to find the ever-popular square root of 2. Then 

   f(x)  =  x2 - 2                                                eq. 5.3-9a
Since we are going to need the derivative of this thing in order to apply the procedure, here it is as well: 
   f'(x)  =  2x                                                   eq. 5.3-9b
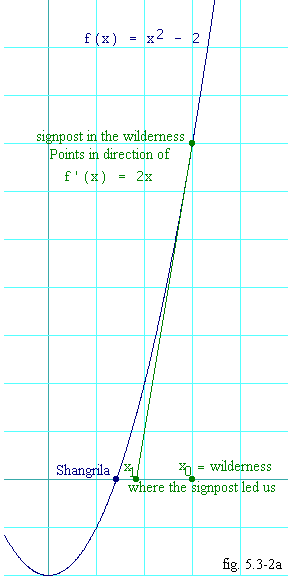Figure 5.3-2a So we pick an arbitrary guess at where Shangrila might be. I'm going to pick x0 = 3. Substituting this into 5.3-9a we get f(x0) = 32 - 2 = 7, which is nowhere close to zero, so apparently we are out in the wilderness somewhere. We also have f'(x0) = 6.

Now we find x1 by applying 5.3-6 to x0. Taking the quotient of f(x0) over f'(x0), we get 1.166666.... Subtracting that from x0 = 3 we get x1 = 1.833333.... And how close did following the signpost get us to Shangrila? We find that by evaluating f(x1). I get f(1.833333...) = 1.361111.... So it seems that this time, the monks have monkeyed with the signposts. We certainly haven't reached Shangrila by following that first one, but we are closer than we were with x0 = 3.

Figure 5.3-2a shows us how the signpost in the wilderness points us. You can see on the graph how our choice of x0 places us in the wilderness. So we start hiking from the point, (x0, f(x0) ). But what direction do we hike in? Well, f'(x0) gives us the slope of the curve at that point. That is the direction we shall go -- along the straight line whose slope is f'(x0) and that passes through the point, (x0, f(x0) ). Of course you can hike in either of two directions along any line. But since we want to end up somewhere on the x axis, we choose the direction that takes us toward it. When we get to the x axis, we see what x value we have arrived at, and that becomes x1.

We are still not at Shangrila yet. So what to do to get closer? Look for another signpost that will get us to an x2. And since eq. 5.3-6 worked so well last time, we do the same thing to x1 to get x2 as we did to x0 to get x1 

               f(x1)
   x2  =  x1 -                                                    eq. 5.3-10
               f'(x1)

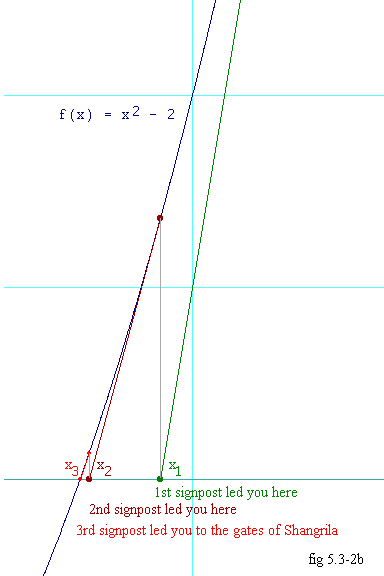
fig. 5.3-2b

We already know that x1 = 1.833333... and that f(x1) = 1.361111... It's easy to figure out that f'(x1) = 2x1 = 3.666666.... From that we can readily apply 5.3-10 to find that x2 = 1.462121......

The brown trace in figure 5.3-2b shows how this procedure is the same as departing from x1 using the derivative as a signpost, and arriving at x2. And how close are we to Shangrila now? With a calculator you can see that f(x2) = 0.137798..., which is closer to Shangrila than f(x1) was. But wouldn't you like to be still closer? How do you think you'd follow the signpost you find at x2 in order to find x3?

Once again, we know x2 and f(x2). It is easy to find f'(x2) = 2x2 = 2.924242.... Again take the quotient of f(x2) over f'(x2), and subtract the result from x2. That will give you x3 = 1.41499842989480.... Fifteen significant figures is all that my calculator gives me. And how close to Shangrila are we now. Well, f(x3) = 0.00220556604515.... Figure 5.3-2b shows x3 to be as close to Shangrila as I am able to plot on this scale.

We can continue iterating the same procedure and get: 

       x4  =  1.41421378004720...

       x5  =  1.41421356237311...
It turns out that x5 differs from the known value of the square root of 2 in only the 15th significant digit. To fifteen figures, the square root of 2 is 1.41421356237310.... What's more, f(x5) is approximately 4.75 × 10-14. If your journey to Shangrila were a thousand miles, you would be within less than a micron of it now.

You may have noticed that with each iteration of this method, the number of digits of accuracy that we had achieved actually doubled. That is a characteristic of this method that is known as quadratic convergence. The method itself is called Newton-Raphson iteration. And you can use it to find the real zeros of any polynomial, no matter how high its degree is.

You can find a brief biography of Isaac Newton by clicking here.

To see for yourself how well this works for finding square roots, get out your calculator. See if you can use the Newton-Raphson iteration method to find the square root of 24 using 5 as a first guess (that is x0 = 5). The polynomial that you are trying to find the zero of this time is 

   f(x)  =  x2 - 24                                                eq. 5.3-11a

   f'(x) =  2x                                                    eq. 5.3-11b
Apply the method for only three iterations, then compare the result (that is your x3) with what the square root key on your calculator gives you for the square root of 24. Not bad, eh?

You will notice that in every problem where we apply Newton-Raphson to taking a square root, f'(x) = 2x. You should be able to demonstrate that quickly by taking the derivative of eq. 5.3-8. Notice that what you get is 2x regardless of the value of C.

Now let's apply Newton Raphson to finding a zero to eq. 5.3-3. You will recall that it is: 

   x3 + 16x2 - 52x - 15  =  0
So we have 
   f(x)  =  x3 + 16x2 - 52x - 15  =  0                            eq. 5.3-12a
And taking the derivative we also have 
   f'(x)  =  3x2 + 32x - 52                                       eq. 5.3-12b
It is useful to know that polynomials of odd degree always have at least one real zero. The same is not true of polynomials of even degree. And if you apply Newton-Raphson to a polynomial that has no real zeros, you will get nowhere. But this one is of odd degree, so let's find one of its zeros. For this demonstration, I will pick x0 = 1. Incidentally, picking x0 actually turns out to be the nasty part of Newton-Raphson iteration when you implement it as a computer program. We'll discuss that more later.

The general equation for Newton-Raphson iteration is 


                 f(xn)
   xn+1  =  xn -                                                  eq. 5.3-13
                 f'(xn)

This means that whenever you have an approximation, xn, that you want to turn into the next better approximation, xn+1, you apply eq. 5.3-13. When you substitute our current f(x) and f'(x) into 5.3-13 you get 

                 xn3 + 16xn2 - 52xn - 15
   xn+1  =  xn -                                                  eq. 5.3-14
                    3xn2 + 32xn - 52
Applying eq. 5.3-14, starting with x0 = 1, I get (on a 15 significant-figure calculator)

Table 5.3-1 
x0  =   1.00000000000000 
x1  =  -1.94117647058824 
x2  =  -0.590015065697130
x3  =  -0.288662835874521
x4  =  -0.267024962511487
x5  =  -0.266907347175526
x6  =  -0.266907343690306
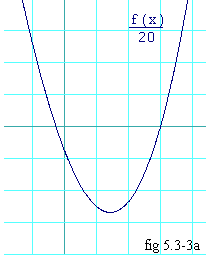
graph of f(x)/20

When I put x6 into f(x) I get zero to 15 significant figures, so there's no need to carry this on any further.

Notice that the successive approximations do jump around a bit at first. That is because 1 might not have been the best choice as a first guess. But by x3, Newton-Raphson had gotten the sign and one significant figure correct. It was rapid convergence from there.

Figure 5.3-3a shows the region of this function near the origin. In the graph, the function is divided by 20 so that it will fit conveniently into the frame. But scaling a function does not change where it's zeros are a bit. Observe that if we had chosen x0 greater than about 1.43, the Newton-Raphson iteration would have converged to something other than -0.266907343690306. Here is the same iteration but starting with x0 = 1.6.

Table 5.3-2 
x0  =  1.60000000000000
x1  =  9.32441860465117
x2  =  5.96893068605278
x3  =  4.10904512385328
x4  =  3.25723966832183
x5  =  3.02008494387405
x6  =  3.00014028560274
x7  =  3.00000000692899
x8  =  3.00000000000000

If you use polynomial long division, you can divide (x - 3.0) out of the f(x) given in eq. 5.3-12a, you get 

     f(x)
              =  x2 + 19x + 5                                     eq. 5.3-15
   (x - 3.0)

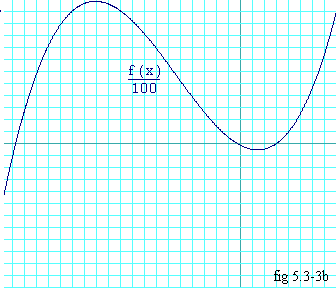
from which you can get the other two zeros by applying the quadratic formula. Figure 5.3-3b gives you a bigger view of the cubic we have solved here by showing f(x)/100 on a larger scale.

Fig. 5.3-3b

Problems

1) Since the 17th century, western music has been based upon the so called well tempered scale. According to this plan, there are twelve notes in each octave (including all the sharps and flats). For example, if you start at C, you have C, #C, D, #D, E, F, #F, G, #G, A, #A, B. After that, it starts over with the C of the next octave (notice that we don't count the C twice, and hence there are twelve notes and not thirteen). Twenty centuries before the advent of the well tempered scale, Pythagoras of the island of Samos in Greece had already discovered that when two musical notes sound an octave apart, the higher one vibrates at twice the frequency of the lower one. He also discovered that what the ear perceives as the pitch interval between notes is actually the ratio of their frequencies, and that two notes that harmonize have a ratio equivalent to the ratio of two small integers.

So much for the background of this problem. The well tempered scale divides the octave (a ratio of 2:1) into twelve equal intervals (which musicians call half-steps). Therefore the ratio of the frequencies of any two adjacent notes (ie, a half step apart) should be that number which, when raised to the twelfth power, gives 2. So what you must do is use the Newton-Raphson method to determine that number. Use 1.0 as your first guess.

View solution

2) Mary is a frugal person and saves her money diligently. She began saving in 1992. In that year, on January 1, she opened a savings account and deposited $1000. On January 1 of 1993, she deposited another $1500. On January 1 of 1994, she deposited $1500 again. On January 1 of 1995, she deposited $2500, and on January 1 of 1996, she deposited $3500. On January 1 of 1997, she checked her account balance before making her next deposit. It was $11953.84. The annual interest rate that the bank had been paying (and to simplify the problem, assume that interest is compounded annually) never changed throughout the time Mary had the account. Use Newton-Raphson to determine what that interest rate is. And don't panic. This problem is not as hard as you think. Think about what is going on with compound interest. See if you can find a polynomial interpretation of this problem.

View solution

Return to Table of Contents

Move on to 5.4 Like a Steam Locomotive (Rolle's Theorem)

email me at hahn@netsrq.com