

Often there is more than one way to attack a problem. Such is the case with the problem of finding the lines tangent to
x2 - 2x + 1that pass through the point, (5,7). Here is the solution that was, until recently, posted on Karl's Calculus Tutor, until a student emailed me with the more direct approach you see posted now.
Step 1: Find the derivative of the curve. In this case we have
y' = 2x - 2We do this because we know that at the point of tangency, the derivative of the curve must be equal to the slope of the tangent line. So we need to know this derivative.
Step 2: Identify the information you get from the point. You are looking for the m and the b of the equation of a line, that is of
y = mx + bthat passes through the point,
7 = 5m + bor equivalently
b = 7 - 5mSo wherever we see b later on, we can substitute
Step 3: Identify what happens at the points of tangency.
You know that if the point,
To find
y = x2 - 2x + 1holds at
Step 4: Make the substitutions into the equation for the line.
Remember the equation for the line is
x2 - 2x + 1 = (2x - 2)x + bBut recall that from step 2, we have
b = 7 - 5(2x - 2) = 17 - 10xPutting it all together you have
x2 - 2x + 1 = (2x - 2)x + 17 - 10x
|
Step 5: Gather like terms and solve for x. Using simple algebra the above equation becomes the quadratic x2 - 10x + 16 = 0You can either use the quadratic formula, or you can factor this one in your head to get (x - 2)(x - 8) = 0So the x coordinate of the the point of tangency is either
Step 6: Substitute back to get m and b.
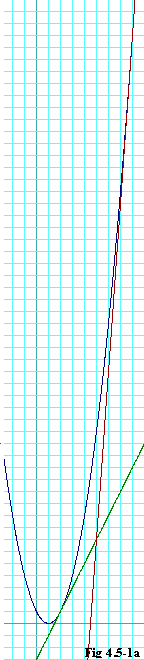
That is, we have already seen that y = 2x - 3and y = 14x - 63and you are done. The curve and the two lines are illustrated in the graph on the right here. Notice where the two lines intersect. Both points of tangency are visible on the graph, although one is very nearly at the top of the graph. |
|
email me at hahn@netsrq.com