Section 4: Derivatives

4.5 The Soft Touch (finding tangent lines)

You've probably already seen it in your homework problems -- "find the equation of the line that is tangent to bloppity-blop curve at the such-and-such point." And if you haven't yet, you soon shall. It will be on the exam as well.

A line that is tangent to a curve has two properties:

The line shares a point with the curve in question.
At the shared point, the derivative of the curve is equal to the slope of the line.

If you solve for those two properties, you have completed the problem.

The equation of a line is, as you learned in algebra

   y  =  mx + b                                                   eq. 4.5-1

So all you have to do is find m and b.

Let's take the second property first. The slope of the line is m. That value has to match the derivative of the curve at the point they give you. So for finding m you need to know the derivative of the curve. And you need to evaluate it at the point they give in the problem. And that value is m.

Then take the first property. You need to find the b that makes that first property true. And you now know what m is equal to. If, for example, the point they want you to be tangent to is (2, 3), then simply take y = mx + b, put in 2 for x, 3 for y, whatever you came up with for m, and solve for b. It's that easy.

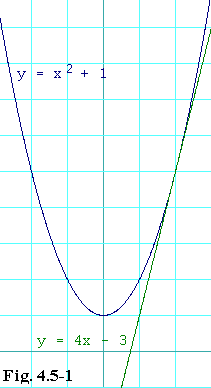
Let's run through an example. Let the curve be

   y(x)  =  x² + 1                                                eq. 4.5-2

Usually it's understood that y is a function of x, so very often this would be written as y = x² + 1. It means exactly the same thing.

Let's find the tangent at x = 2. So what point is that? We know the x-coordinate of the point. To find the y-coordinate, simply use the equation of the curve (given in 4.5-2). That gives us y = 5, so the point that we want our line to be tangent at is (2, 5).

Step 1: Find the derivative of the curve. The equation of the curve is given in 4.5-2. You know how to take its derivative. It's

   y'(x)  =  2x                                                   eq. 4.5-3

Step 2: Evaluate the derivative at the point given. The problem says do it at x = 2. The derivative at that x is y'(2) = 4. That is your m. Write it down. m = 4.

Step 3: Solve for b. Remember, y = mx + b. We know what x is, what y is, and what m is. If you plug them all in, you get

   5 = 4×2 + b                                                    eq. 4.5-4a

And it's trivial algebra to go from there to

   b = -3                                                         eq. 4.5-4b

Step 4: Write the equation. You know m and b now. Simply substitute them into y = mx + b. You get

   y = 4x - 3                                                     eq. 4.5-5

That's it. We're done. Once you know how to take the derivative, these problems are easy. Just follow the four steps here.

Figure 4.5-1 shows a graph of this problem. Observe how the tangent line just kisses the curve at `(2, 5)`. The angle they meet at is, in fact, zero. Plotting the curve and the tangent line is one way you can check your work to see if your answer is right. Another way is to substitute the `x` given in the problem (in this case `2`) into the equation for your line and see if you get back the same `y` (in this case `5`) as you get by substituting that `x` into the equation for the curve. Indeed, in this problem, `x² + 1 = 4x - 3 = 5` when `x = 2`. In addition, you should have that the slope of the line equals `y'(x) = 2x = y'(2) = 4` for this problem. But that test can hardly fail, since that's how you chose the slope of the line in the first place.

Figure 4.5-1 shows a graph of this problem. Observe how the tangent line just kisses the curve at (2, 5). The angle they meet at is, in fact, zero. Plotting the curve and the tangent line is one way you can check your work to see if your answer is right. Another way is to substitute the x given in the problem (in this case 2) into the equation for your line and see if you get back the same y (in this case 5) as you get by substituting that x into the equation for the curve. Indeed, in this problem, x² + 1 = 4x - 3 = 5 when x = 2. In addition, you should have that the slope of the line equals y'(x) = 2x = y'(2) = 4 for this problem. But that test can hardly fail, since that's how you chose the slope of the line in the first place.

Here's a slightly more complicated variant on the same problem. Find the two lines that are tangent to

   y  =  x² - 2x + 1

and pass through the point, (5, 7). Observe that in this case, the point, (5, 7), does not lie on the curve. So you are finding lines that pass through a point outside the curve but at some other points, which are as yet unknown, they are tangent to the curve. The strategy is to identify those points of tangency. From them, it is easy to find the lines that solve the problem.

Step 1: Find the derivative of the curve. In this case we have

   y'  =  2x - 2

We do this because we know that at the point of tangency, the derivative of the curve must be equal to the slope of the tangent line. So we need to know this derivative.

Step 2: Write as much of the equation of the line as you can from what you know. The slope, m, of the line is still unknown. But you know what point it must pass through. In this case that is the point (5,7). So using the formula for the equation of a line passing through a given point with a given slope, you have:

   y - 7  =  m(x - 5)

Step 3: Use the derivative to write an equation for the slope. We don't know the slope of the line yet, but we know that if the point, (x,y), is the point of tangency, then the slope of the line will be equal to the derivative of the original curve at x. The derivative we already determined to be y' = 2x - 2. So we write the equation

   m  =  y'  =  2x - 2

Step 4: Substitute the slope expression into the equation for the line. You have m = 2x - 2 and y - 7 = m(x - 5). Put them both together by substituting for m in the second equation.

   y - 7  =  (2x - 2)(x - 5)  =  2x² - 12x + 10

   y  =  2x² - 12x + 17

Step 5: Substitute the equation for the original curve back in. That is, you know that y = x² - 2x + 1, where (x,y) is the point of tangency. Why? Because the point of tangency must lie on the curve. Substituting that expression for y into the above gives:

   x² - 2x + 1  =  2x² - 12x + 17

Step 6: Gather like terms and solve for x. Using simple algebra the above equation becomes the quadratic

   x² - 10x + 16  =  0

You can either use the quadratic formula, or you can factor this one in your head to get

   (x - 2)(x - 8)  =  0

So the x coordinate of the the point of tangency is either x = 2 or x = 8.

Step 7: Substitute back to get m. That is, we have already seen that m = 2x - 2 at any point, (x, y), of tangency. Since we now know what both the x's are for the points of tangency, we can put those values into the equation for m and get that either m = 2 or m = 14. From the equation we had in step 2,

   y - 7  =  2(x - 5)

and

   y - 7  =  14(x - 5)

When you multiply those out and put them into slope-intercept form, the equations of the two lines that are tangent to y = x² - 2x + 1 and pass through the point, (5, 7), are

   y  =  2x - 3

and

   y  =  14x - 63

and you are done. The curve and the two lines are illustrated in the graph on the right here. Notice where the two lines intersect. Both points of tangency are visible on the graph, although one is very nearly at the top of the graph.

Click here to see an alternative attack on this same problem.

Finding the Normal Line

This is one they might throw at you just to keep you on your toes. Instead of asking for the equation of the tangent line, they'll ask you for the equation of the line that is normal to bloppity-blop curve at such-and-such a point.

How much do you remember from algebra? Do you remember that if two lines are normal to each other (that is, they are at right angles to each other), then their slopes are negative reciprocals of each other? In other words, if one has a slope of m, then the other must have slope of -1/m. Can you extend this definition to include a line being normal to a curve? It's just a small variation of the rules we had for tangent lines.

The line shares a point with the curve in question.
At the shared point, derivative of the curve is the negative reciprocal of the slope of the line.

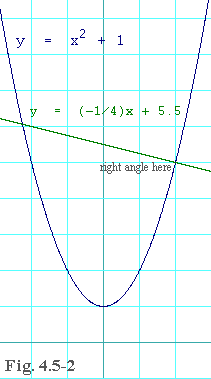
Let's take our example from before where the curve is y = x² + 1 and we want the normal line to pass through (2, 5). Step 1 is the same as before. It is still the case that y' = 2x. In step 2, though, after we evaluate y'(x) at x = 2 and find that it's equal to 4, instead of setting m to that, we set m to its negative reciprocal, which is -1/4.

The remaining steps are the same. Solve for b with the x and y coordinates you have and the m you have just determined. In this case we have:

   5  =  (-1/4)×2 + b                                             eq. 4.5-6a

and solving for b, we have

   b  =  5.5                                                      eq. 4.5-6b

So the answer here is

   y = (-1/4)x + 5.5                                              eq. 4.5-7

Figure 4.5-2 shows a plot of our curve and the line that is normal to it at `x = 2`. Observe that the normal line crosses our curve in two places. At `(2, 5)` is the crossing at right angles that we expected to get. To the left there is another crossing at a point we have not determined yet. On a homework problem or on a test, you may be asked to identify this second crossing. But that is just an algebra problem. Recall that to find where the plots of two functions cross you simply take the difference of the two functions and solve for the `x` that makes the difference be zero. Our two functions are `y = x² + 1` and `y = (-1/4)x + 5.5`. Write down the expression for the difference between them, and then scroll down.

Figure 4.5-2 shows a plot of our curve and the line that is normal to it at x = 2. Observe that the normal line crosses our curve in two places. At (2, 5) is the crossing at right angles that we expected to get. To the left there is another crossing at a point we have not determined yet. On a homework problem or on a test, you may be asked to identify this second crossing. But that is just an algebra problem.

Recall that to find where the plots of two functions cross you simply take the difference of the two functions and solve for the x that makes the difference be zero. Our two functions are y = x² + 1 and y = (-1/4)x + 5.5. Write down the expression for the difference between them, and then scroll down.

You should either have for your difference

   x² + (1/4)x - 4.5                                              eq. 4.5-7a

or the negative of that. The perscription then is to set that equal to zero and solve for x.

   x² + (1/4)x - 4.5  =  0                                        eq. 4.5-7b

This is without a doubt a quadratic polynomial and we have the quadratic formula with which to solve it. We get

                 _________
         -1/4 ± Ö1/16 + 18
   x  =                                                           eq. 4.5-8
                 2

If you take the plus of the ±, you get x = 2. And one of the solutions had better be x = 2, since we already determined that to be the right-hand intersection point. If you take the minus of the ±, you get x = -9/4 = -2.25. Plug that back into the original equation for the curve and you get y = 97/16 = 6.0625. So the left-hand intersection is at (-2.25, 6.0625). You can look at the graph to confirm this.

Exercise

Let

             ______
   y(x)  =  Ö1 - x²

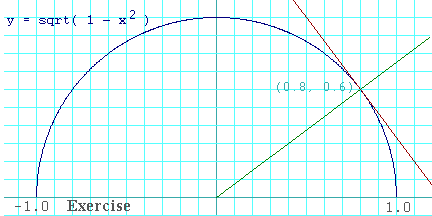
The graph of this is shown in the figure to the right. You probably recall from algebra that this function has a graph that is a semicircle. Find the equations of both the tangent line and the normal line at x = 0.8. Then, without appealing to the geometry of semicircles, but using only derivatives and algebra, show that every line normal to this function goes through the origin no matter what point on the curve it passes through.

Step 1: Find the derivative of the function. You will need it for every step after this one. Notice that this function is a composite of y(x) = f(g(x)), where

             _
   f(x)  =  Öx

and g(x) = 1 - x². Because it is a composite, you will need to apply the chain rule in order to find y'(x). At this point I am not going to give away this derivative -- you should be able to do it yourself. I will remind you that if

             _
   f(x)  =  Öx

then

              1
   f'(x)  =     
             2Öx

which is useful to know in finding the derivative of y(x).

Step 2: Where is the point of tangency? Simply substitute the x given in the problem into the function to get a value for y(x). You shouldn't have to think too hard, because I gave it away in the diagram.

Step 3: What is the slope of the tangent line? of the normal line? Remember that the slope of the tangent equals the derivative of the function at the point of tangency. So stick the value given for x into the equation you have for y'(x) to find that value. That is the m for the tangent line. It's negative reciprocal is the m for the normal line.

Step 4: Solve for b in both cases, that is the b for the tangent line and the b for the normal line. Remember that you now know the m's for both of them as well as an x and corresponding y. Just substitute them into y = mx + b and solve for b.

That completes the problem for both finding the tangent and the normal. So write your y = mx + b equations for each, substituting the values you found for m and b into each. Did you get b = 0 for the normal line? If you didn't you made a mistake. If you did, you are ready to attack the second part of the problem. Show that when you compute the normal equation for any point on this curve, the b is always zero.

Simply write y = mx + b, but substitute the expression for negative reciprocal of slope in for m and substitute the expression given in the problem for y(x) in for y. Take all the cancellations you can. You should end up with b = 0 standing all alone.

Return to Table of Contents

Move on to Hilltops and Valley Floors

email me at hahn@netsrq.com