Section 6: Exponentials and LogrithmsKCT logo

© 1997 by Karl Hahn

6.2 The Farther We Go, The Faster We Get There

Return now to the example of that bacteria that doubled its numbers every 60 minutes. Remember that after 10 hours, a single bacterium had multiplied into 1024 (that is 210). In the 11th hour, we expected that the population would increase from 1024 to 2048 (that is to 211), for a net increase of 1024.

In fact, in any hour, the net increase is we expect precisely the amount there were at the beginning of the hour. But what is the increase we expect in, say, half an hour? If the population grows in 1 hour to 21 times what it was, then in half an hour, we expect it to grow to 20.5 times what it was. And from our discussion in the last section, we know that 20.5 is in fact  Ö2 = 1.41421356... So the population after 10.5 hours ought to be 1024 × 1.41421356... = 1448.15... The net increase in that half hour is 

   (1024 × 1.41421356) - 1024  =  1024 × (1.41421356 - 1)  =  424.15
What I'd like you to notice is not the 424.15, but the middle expression. Notice that it is the product of the starting amount and Ö2 - 1. And it doesn't matter which half hour you examine. The net increase is still the starting amount times that number. If, for example, you looked at the half hour that elapses from 16 hours to 16.5 hours, we see that the starting amount is 65536 (that is 216). The net increase in that elapsed half hour is  65536 × (Ö2 - 1) ) = 27145.9.

And what about the net increase in a quarter-hour period? We expect that if there are n at the beginning of the quarter-hour, then at the end of the quarter-hour there ought to be n × 20.25. Hence the net increase in that time is  n × (1 - 20.25)  (by the way, if you hadn't already figured this out, 20.25 is the same as Ö(Ö2) -- the square root of the square root of 2). Again the point is that it doesn't matter which quarter hour you choose. The net increase is always in direct proportion to the number of bacteria present at the beginning of the quarter hour.

Remember also that we determined that if the bacteria colony is allowed to grow unchecked for several days, the population would grow so large that cell divisions would be taking place in even the shortest imaginable time intervals. Still you would find that even over a millisecond, the net increase in population would continue to be in direct proportion to the population at the start of that millisecond. One millisecond is 0.0000002778 hours. So if there are n bacteria at the beginning of a millisecond, there should be n × 20.00000002778 at the end of the millisecond, for a net increase of n × (20.00000002778 - 1). My calculator says that (20.00000002778 - 1) is approximately equal to 0.00000001925. So if there were a billion (that is a thousand million) bacteria, a millisecond should bring forth 192.5 more. If there were ten billion, a millisecond should bring forth 1925 more.

This is the operative property of all exponentials: the rate of increase is always in direct proportion to the exponential itself. And in place of the phrase rate of increase we can substitute the word derivative. We have demonstrated the truth of this informally with our discussion of the bacteria colony. We now go on to demonstrate it mathematically. Warning: The derivation that follows is likely to be on the exam.

Recall from section 4.1 how we define a derivative. 

             df             f(x + h) - f(x)
   f'(x)  =      =    lim                                         eq. 4.1-2
             dx      h  > 0        h
If you wanted to know the derivative of the function 
   f(x)  =  2x                                                    eq. 6.2-1
for example, you would substitute 2x for f(x) into eq. 4.1-2. Where you see f(x+h) you would substitute 2x+h. And you get 
                     2x+h - 2x
   f'(x)  =    lim                                                eq. 6.2-2
              h  > 0     h
By taking this limit as h goes to zero, the derivative of 2x should emerge.

But how do you take that limit? First we can apply the basic rule of exponents that we developed in the last section. Notice that we have a term, 2x+h. And recall we had a rule about the sum of exponents. 

   2x+h  =  2x × 2h                                               eq. 6.2-3
If you substitute this in for 2x+h, 6.2-2 becomes 
                      (2x × 2h) - 2x
   f'(x)  =     lim                                               eq. 6.2-4
               h  > 0        h
Notice that the two terms in the numerator have a common factor of 2x. If you factor that out, you get 
                      2h - 1
   f'(x)  =     lim          × 2x                                 eq. 6.2-5
               h  > 0    h
Remember also the product rule for limits (that is, the limit of the product is equal to the product of the limits). So the above is the same as 
                      2h - 1
   f'(x)  =     lim           ×    lim   2x                       eq. 6.2-6
               h  > 0    h        h  > 0
Look carefully at the two limits in eq. 6.2-6. The limit on the left has no x's in it. That means that it is independent of x. In other words, no matter where you take the derivative of  f(x) = 2x, this term will always be the same number. By contrast, the limit on the right has no h's in it. So it is equal to 2x, no matter how close to zero h gets. Clearly the limit on the right is simply 2x. So by taking that limit and rearranging, we have 
                          2h - 1
   f'(x)  =  2x ×   lim                                           eq. 6.2-7
                   h  > 0    h
This makes it quite clear that the derivative of  f(x) = 2 x is always proportional to 2x. The limit on the right (assuming of course that it exists) always goes to the same number, and always gives you the same multiplier to apply to 2x. The only question is, what is that multiplier? 
                                  2h - 1
        h                               
                                     h

      0.1                         0.71773...
      0.01                        0.69555...
      0.001                       0.69339...
      0.0001                      0.69317...
      0.00001                     0.69314...
      0.000001                    0.69314...

               Table 6.2-1
The table seems to indicate that limit exists for the limit on the right-hand side of 6.2-7, at least to 5 places beyond the decimal point. Assuming that it does, we can say that the derivative of  f(x) = 2x  is  f'(x) = 2x × 0.69314...

And we needn't restrict ourselves to 2x. Pick any positive real number, b. You can run the same derivation on f(x) = bx simply by replacing all the 2's with b's: 

                     bx+h - bx
   f'(x)  =    lim                                                eq. 6.2-8
              h  > 0     h




                      (bx × bh) - bx
   f'(x)  =     lim                                               eq. 6.2-9
               h  > 0        h




                      bh - 1
   f'(x)  =     lim          × bx                                 eq. 6.2-10
               h  > 0    h




                      bh - 1
   f'(x)  =     lim           ×    lim   bx                       eq. 6.2-11
               h  > 0    h        h  > 0




                          bh - 1
   f'(x)  =  bx ×   lim                                           eq. 6.2-12
                   h  > 0    h
Again, the derivative of  f(x) = bx  is equal to bx times whatever constant that limit on right goes to.

This limit of 

           bh - 1
     lim                                                          eq. 6.2-13
    h  > 0    h
is so important that we give it a special name. We call it ln(b), which is an abbreviation for natural log of b. We shall be studying the natural log intensely in the next section. Perhaps you have already heard of the ln function before, or perhaps your instructor has approached it in a different way. That's ok. There are many roads to the ln function, and in this tutorial I intend to show them all, and more importantly, why they are all equivalent. Using this shorthand for the limit in 6.2-13, we can say that when  b > 0  and  f(x) = bx 
   f'(x)  =  bx × ln(b)                                           eq. 6.2-14
which is simply the the exponential, bx, times a constant.

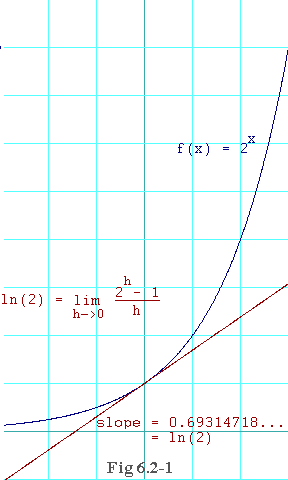
Graph of 2^x

Figure 6.2-1 shows a plot of  f(x) = 2x. It is shown with a line tangent to it at the point (0, 1). That line has a slope of  ln(2) = 0.69134718.... To find the slope of this curve anywhere else, simply take the y-coordinate and multiply it by ln(2). With a calculator and a judicious eyeball, you can even see (at least approximately) that this is true.

Important Points

  1. The derivative of an exponential is always that same exponential times a constant.
  2. The constant is always the natural log of the base (the base, b, being the positive real number to which the exponent is applied -- e.g. bx).
  3. For the purposes of this tutorial, we define the natural log of b according to the limit given in 6.2-13 (and we abrieviate it as ln(b)).
All of this is a direct consequence of a) the definition of a derivative given in 4.1-2, and b) the rule of exponentials that tells us bs+t = bsbt. And you should be able to show the logic that connects these facts with the three points given above, because you may be asked to do so on an exam.

Exercises

1) Let a and b be any positive real numbers. Apply the product rule to 

   f(x)  =  ax bx
to determine its derivative. Use the shorthand, ln(a) and ln(b), where appropriate. Once you have an expression for f'(x), recall the rule you proved at the end of section 6.1 concerning ax × bx. Take the derivative of 
   f(x)  =  (ab)x
What special property of ln(ab) can you infer from all this? Click here to see the solution, but make an honest effort to work it out yourself first.

2) Use the chain rule to determine the derivative of 

   f(x)  =  bcx
where b is any positive real number and c is any real number. Once you're done with that, observe from our discussion in the last section that 
   bcx  =  (bc)x
Find the derivative of the right-hand expression above. What other special property of ln(bc) does this suggest? When you are done working this, click here to see the solution.

3) Take everything you did in the second problem and simply substitute the expression, 1/ln(b), for every occurrence you find of c. Take whatever cancellations you can. What unusual and mathematically interesting relationship do you now find between the resulting function and its derivative? When you see an interesting property and you think it's the one I'm after, click here.

4) Use the product rule to determine the derivative of 

            x2
   f(x)  =     bx
            2
where b is any positive real number. When you are done applying the product rule, you will see that the result has something you can factor out. Do so. When you are done, click here to see if you got the right answer.

5) Use the chain rule to determine the derivative of 

   f(x)  =  b-x2
where b is any positive real number. Make your best effort, then click here to see if you got it right.

6) Let b be a positive real number and let n be a counting number. Suppose you didn't know what a particular f(x) was, but you knew that the equation, 

   bf(x)  =  xn
always holds. Use implicit differentiation (which is really just an application of the chain rule) to find the derivative of f(x). Hint: Once you have applied implicit differentiation, there will be a substitution you can make using the original equation for f(x) that will enable you to simplify the result. The simplicity of the final answer will surprise you. Click here when you are done.

Return to Table of Contents

Move on to Be Frugal and Add (logrithms)

email me at hahn@netsrq.com