Karl's Calculus Tutor - Solution to Exercise 8.2-5

Solution to Exercise 8.2-5KCT logo

© 1999 by Karl Hahn

The problem was: Two sticks, one 8 feet long, the other 12 feet long, are joined end-to-end with a hinge. The free end of the 8 foot stick is fixed to the ground. The free end of the 12 foot stick is slid along the ground toward the free end of the 8 foot stick at one foot per second. The whole assembly is held so that the triangle formed by the two sticks and the ground is always perpendicular to the ground. At what rate is the angle between the 8 foot stick and the ground increasing when the distance between the free ends of the two sticks is 5 feet?

The hint was to use the law of cosines.

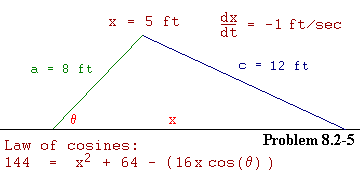
The first thing to do here is make a diagram. Here's mine. If you made a diagram, you probably got something like this, but you probably didn't do it in color. Here the 8 foot stick is shown in green, the 12 foot stick in blue. The distance between the far ends of the stick (that is along the ground) is x. The angle the problem talks about is q. Again the diagram is not drawn to scale, and your diagram need not be drawn to scale either in order for it to be useful in tackling this problem. Besides, without the aid of a compass, it would be hard to draw this one to scale because we do not yet know the value of q.

Answer to question 1 again is that time, t, is the independent variable. And to question 2, clearly x and q are the dependent variables. And to question 3, there are no hidden variables.

And now to question 4 -- what is the relationship between x and q? This is given by the law of cosines. When you plug in the parameters of this problem, you get 

   c2  =  x2 + a2 - (2ax cos(q) )                                 eq. p5.1a
or in numbers, as is shown in the diagram: 
   144  =  x2 + 64 - (16x cos(q) )                                eq. p5.1b

Now comes question 5, and things get just a little dicey. You do have to use the product rule in order to take the derivative of the right-hand term of equation p5.1a. 

            dx                dq               dx
   0  =  2x     +  2ax sin(q)     -  2a cos(q)                     eq. p5.2
            dt                dt               dt
The problem asks for dq/dt, so in answering question 6, you need to figure out a way to solve for that based upon what the problem gives us, which is a value for x and a value for dx/dt. The difficulty, of course, is that your solution must involve cos(q) and sin(q). But using the law of cosines equation (eq. p5.1a), you can solve for cos(q). 
   c2  =  x2 + a2 - (2ax cos(q) )                                 eq. p5.1a


              x2 + a2 - c2
   cos(q)  =                                                      eq. p5.3
                  2ax
and from that you can readily find sin(q) using the identity: 
                 ___________
   |sin(q)|  =  Ö1 - cos2(q)                                      eq. p5.4
Since q can be no more than p radians (180 degrees), we are guaranteed that sin(q) will be positive, and so we can drop the absolute value in the above.

When you solve eq. p5.2 for dq/dt you get 

   dq     2a cos(q) - 2x  dx
       =                                                          eq. p5.5
   dt       2ax sin(q)    dt
Finally to question 7 -- putting in the numbers. The problem gives us that x = 5. From the diagram we have a = 8 and c = 12. From this equation, p5.3 gives you that cos(q) = -55/80 = -0.6875. From that and equation p5.4 you have that sin(q) = 0.726184377. We know that x is decreasing at a rate of 1 foot per second, so dx/dt = -1. Putting that all into equation p5.5 you have 
   dq
       =  0.361478445 radians/second  =  20.71118932 degrees/second
   dt
Note that the rate is positive, so q is increasing. Does that seem reasonable if x is decreasing? Refer back to the diagram.

Note also that starting with equation p5.1b you could have carried numerical values down into the subsequent equations instead of the symbols, a and c. If you made no mistakes you would have ended up with the same answer. In general, though, it is not a good idea to do this. If you carry the symbols down, reaching a fully symbolic solution right up until the last steps (e.g., equation p5.5), not only are you immune to a greate many arithmetic mistakes you might have made otherwise, but you also have an opportunity to do dimensional checking on your solution.

Return to Main Text

email me at hahn@netsrq.com