

If you have read The Little Prince by Antoine de Saint-Exupéry, then you remember when the Little Prince first appears, he asks the narrator to draw him a sheep. The first sheep the narrator draws is too sickly. The second is, in the Prince's estimation, a ram. The third is too old. Finally, not knowing exactly what the Little Prince wants, the narrator draws a box and tells him that the sheep is inside. And the sheep inside turns out to be just what the Little Prince had in mind.
In your past math classes you have been asked more often than you'd like to recall to draw a graph of this function or that function. And how often have the graphs you've drawn been too steep or too angular or the wrong shape or had some other fatal defect? And now in introductory calculus you are likely to be asked again to draw the graph of this or that function. If only you could just draw a box and assure your instructor that the graph he wants is inside.
But one thing has changed this time about your being asked to draw graphs, and that is the instructor's agenda. What you have learned about limits and derivatives will, if you apply it correctly, supply you with a box that only the graph you instructor asks for will fit into. And that's the point. By observing the calculus properties of functions, you will be able to determine a lot about a function's graph before you ever plot the first point -- things like where it has assymptotes, where it has maximums and minimums, where it has inflection points -- these form the box. And not many wrong answers will fit into that box.
The best thing to do is to jump right in and try one. Let's do
x2 + 1
f(x) =
x2 - 4x + 3
The graphing problems that appear on homeworks and exams
usually give you hints by asking you to identify where
the graph is increasing, where it is decreasing, where
the critical points are, whether the critical points are
maximums or minimums, and where the horizontal and vertical
assymptotes are.
The function we have here falls into the category of being
a rational function. That is, it's the ratio of two polynomials.
When you get one of these, the first thing to do is to try
to factor the polynomials -- especially the denominator.
Here, the numerator is
x2 + 1
f(x) =
(x - 1)(x - 3)
is entirely equivalent to the original function. This gives you
your first clues about the behavior of this function. Observe
that the denominator has zeros at
We can find out much more about the function by looking at
its derivative. Since f(x) is a ratio, we have to
use the
(x2 - 4x + 3)(2x) - (x2 + 1)(2x - 4)
f'(x) =
(x2 - 4x + 3)2
When you multiply out the numerator and gather up like terms, you
find that the x3 terms cancel and you are
left with
-4x2 + 4x + 4
f'(x) =
(x2 - 4x + 3)2
Observe that the denominator is squared and therefore it is
never negative. So you can determine where the derivative is
positive or negative soley by analysing the numerator of
f'(x). And knowing
where f'(x) is positive and negative will tell you where
the function is increasing and decreasing respectively.
The best way to find out where f'(x) is positive and negative
is to find where it is zero. Again, where it is zero is almost entirely
dependent on the numerator. The denominator cannot cause the function
to be zero. So we look for where the numerator is zero. To do this we use
the
_
1 Ö5
x = ±
2 2
In decimals, that's approximately
Now we put the critical x's back into f(x) (you'll want a calculator to do this).
f(-0.61808339) = 0.2360679 f(1.61808339) = -4.2360679These two points ( (-0.61808339,0.2360679) and (1.61808339,-4.2360679)) will be points on the graph, so you might as well plot them. Label them as critical points. And that means that the trace of the graph will be horizontal as it passes through each them.
Two critical points divide the domain (that is the set of
all possible x's) into three regions. The first is
where
f'(-1) = -1/16 f'(0) = 4/9 f'(2) = -4/1This means that in the first region, f(x) is decreasing because f'(x) is negative in that entire region. In the second region, f(x) is increasing because f'(x) is positive in that entire region. In the third region, f(x) is decreasing again because again f'(x) is negative for that entire region.
This also tells us which of the critical points is a minimum and which is a maximum. When x is less than the critical point, -0.61808339, f(x) is decreasing, and when x is just a bit greater than that critical point, f(x) is increasing. Think about it. On both sides of the critical point, f(x) must be more than what it is at the critical point. This clearly indicates that this critical point is a minimum. Likewise, when x is greater than the critical point, 1.61808339, f(x) decreasing. In the region where x is less than that critical point, f(x) is increasing. So on both sides of this second critical point, f(x) must be less than what it is at the critical point. This indicates that the second critical point is a maximum.
Finally look at the original f(x) one more time.
x2 + 1
f(x) =
x2 - 4x + 3
If you take the limit as x goes to either infinity or
to minus infinity, notice that the terms that become dominant
are the x2 in the numerator and the
x2 in the denominator. All other terms
become insignificant compared to these two. So in the limit
(in either direction) you end up with
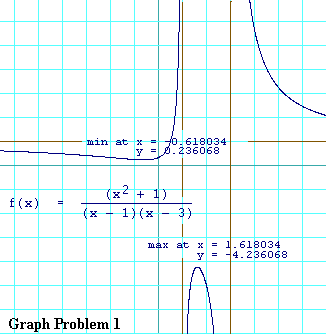
Here, at last, is the graph itself. Look at what happens
at each of the vertical assymptotes (which are shown in
brown). In the region of the first one (where
If you make all of the observations we have made here and plotted just the two critical points, you can get the correct shape for the rest of the graph without using your calculuator at all beyond plotting those two points.
The important thing to remember here is that the sign of f'(x) will not change as a result of x passing through a simple zero of the denominator of f(x) (provided the numerator does not also have a zero at the same x). That is why the method we used worked. The same cannot be said about x passing through a double zero of the denominator.
If you did not know this rule, then the safest thing for you to do would be to divide the domain of f(x) into more regions. Again use each zero of f'(x) as a dividing point between regions. But also use each vertical assymptote as a dividing point as well. In this problem that would give you five regions:
f'(-1) = -1/16 f'(0) = 4/9 f'(3/2) = 16/9 f'(2) = -4/1 f'(4) = -44/9From this table you can see that f'(x) changes sign only at
Here's another example:
_____
f(x) = Ö1 + x (x2 - x - 4)
The typical problem might read:
Graph f(x) finding all zero crossings, regions where f(x) is increasing and decreasing, all critical points, and whether they are maximums, minimums, or neither. In addition, describe what f'(x) does as x approaches -1 from above.
Step 1: Determine the domain of f(x). The sqrt function does not admit negative arguments. So what restrictions does that place on x? When you decide what the domain is, click here.
That was pretty easy, eh? You should have gotten that the domain is everywhere where
Step 2: Find where f(x) is zero. This will determine the crossing points. Remember that for a product to be zero, one or both of its factors must be zero. Work out where the zero crossings are, then click here.
You were looking for every place every place that either
__
1 Ö17
x =
In decimals that's approximately
±
2 2
x = -1
x = 2.56155813
Mark them on your graph along the x axis.
This is all well and good, but so far all we have done on this
function is algebra. Now it's time to do some calculus.
Step 3: Find the derivative of f(x).
Since f(x) is a product of
The derivative of
1
2Öx + 1
And the derivative of
_____ 1
f'(x) = Öx + 1 (2x - 1) + (x2 - x - 4)
2Öx + 1
Step 4: Find where f'(x) is zero.
That's where the critical points will be. So you will rewrite the
above equation, but replace the symbol, "f'(x)", with
zero. Then you are going to solve the equation that results for
x. Hint: Multiply through by
If you followed the hint, you would have been solving the equation
0 = 2(x + 1)(2x - 1) + (x2 - x - 4)When you multiply out the left-hand summand you get
0 = 4x2 + 2x - 2 + x2 - x - 4and on gathering like term you get
0 = 5x2 + x - 6Again the quadratic formula comes to your aid. You find that
___
1 Ö121
x = ±
10 10
So x is either -12/10 or 10/10. Since -12/10
is less than -1, it is outside the domain of f(x), so we
discard that solution. That leaves the only critical point at
_
f(1) = -4Ö2 = -5.656854249...
Step 6: Using what you know about f'(x), divide up the domain of f(x). This function has no zeros in its denominator because it has no denominator. So the only thing there is to divide it up is the one critical point. This should be easy. Click here when you're ready.
One division point can only mean that you divide the domain of f(x) into
two regions, one less than the division point, the other greater than the
division point. The division point, in this case, is
The domain of f(x) you already determined was restricted to
Step 7: Pick a sample point in each region and evaluatef'(x) at
each sample point. This should be easy. The only hint I'll give you is to observe
that the region,
I picked
f'(0) = -3
_
_ Ö3
f'(2) = 3Ö3 +
3
This indicates that in the region,
Step 8: Plot the graph.
You now know where the graph is increasing, decreasing, where its zeros
are, and where its minimum is. You should be able to make a rough plot
incorporating all these features. Remember that on the left side of the
graph,
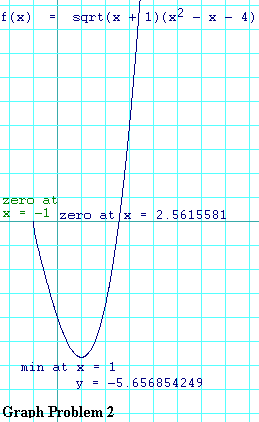
There you have it. Give yourself full credit if you got the general shape right as well as where the minimum is and where the zero crossings are.
Finally the question asked what happens to f'(x) as x approaches
-1 from above. Look again at the expression for f'(x)
(click here to see that equation again).
Observe that it has a denominator term of
Graph the function
x
f(x) =
1 - x2
identifying all horizontal and vertical assymptotes, all zero crossings,
all critical points (and whether they are maximums or minimums), and all inflection points.
Step 1: Factor the denominator. This will tell what the domain
of this function is and where the vertical assymptotes are.
The denominator factors according to the
x x
f(x) = =
1 - x2 (1 + x)(1 - x)
This shows that the denominator has zeros at
Step 2: Identify the zero crossings. Remember that only the
numerator being zero can make a quotient be zero. When you find an x
where the numerator is zero, remember to test the denominator at that x
as well. That's because you can't have a zero crossing at an x where
f(x) is undefined. When you are done,
The numerator of f(x) is simply x, and that has a zero only
at
Step 3: Find the derivative of f(x). You will need that to determine where the critical points are. Here is f(x) again so that you can view it while you're working on the first derivative.
x
f(x) =
1 - x2
You should have used the
(1 - x2) - x(-2x) 1 - x2 + 2x2 1 + x2
f'(x) = = =
(1 - x2)2 (1 - x2)2 (1 - x2)2
Step 4: Find the critical points.
Remember that they occur only where f'(x) is zero.
Remember also that f'(x) can only be zero at x's where
its numerator is zero. When you have figured this part out,
The numerator expression for f'(x) is
You can very easily, though, determine that
Step 5: Find the second derivative of f(x). You will need this in order to identify inflection points. Here is the first derivative again so that you can view it while you're working on the second derivative:
1 + x2
f'(x) =
(1 - x2)2
When you are done calculating and simplifying,
Again you had to apply the
(1 - x2)2(2x) - (1 + x2)2(1 - x2)(-2x)
f"(x) =
(1 - x2)4
2x - 4x3 + 2x5 + (4x)(1 + x2)(1 - x2)
=
(1 - x2)4
Observe that the right-hand term in the numerator multiplies out to a difference
of squares.
2x - 4x3 + 2x5 + (4x)(1 - x4)
f"(x) =
(1 - x2)4
2x - 4x3 + 2x5 + 4x - 4x5
=
(1 - x2)4
-2x5 - 4x3 + 6x -2x(x4 + 2x2 - 3)
= =
(1 - x2)4 (1 - x2)4
Step 6: Determine the inflection points. Remember that they are where
To find the inflection point(s), you had to determine where the numerator of f"(x) was zero. The numerator was
-(2x)(x4 + 2x2 - 3)Clealy this expression is zero when
u2 + 2u - 3which you can factor either in your head or by using the
(u + 3)(u - 1)Substituting back the x2 for u, you get
(x2 + 3)(x2 - 1)So what values of x lead to this expression being zero? Well either
Step 7: Find the limits of
f(x) as x goes to infinity and minus infinity.
You will need this information for finding the horizontal assymptotes. Also pay attention
to whether f(x) is positive or negative as x gets big in the positive
direction or in the negative direction. When you have pondered this and come to a conclusion,
x
f(x) =
1 - x2
Observe that the highest order term in the numerator is x and the
highest order term in the denominator is x2. So as the
magnitude of x gets big in either direction, the denominator's
magnitude will get big faster than the numerator's. The limit in either
direction can only be zero. So to the left, the trace of f(x)
will have to approach
But which side of
Step 8: Plot the graph using all the facts you have discerned
so far. Go ahead and do so, then
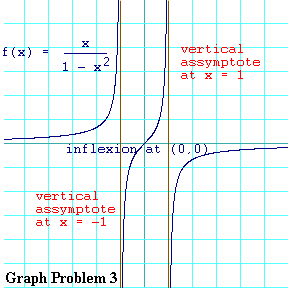
Well here it is. From left to right, the explanation: When x
is very negative, we know that f(x) is near zero but positive.
We also know that it does not cross the y axis anywhere left of
the vertical assymptote at
In the region between the two assymptotes we know that f(x)
continues to slope up. So just to the right of the vertical assymptote
at
Finally in the region to the right of the vertical assymptote
assymptote at
Some final notes: If you study the expression for f(x) you will see that
it is an odd function -- that is
If you were ambitious about getting the shape of the graph more accurately,
you could, for example, have determined what values of x the slope
of the trace is equal to 1. You already know one point where
this happens, and that is at
1 + x2 (1 - x2)2 1 + x2 - 1 + 2x2 - x4 -x4 + 3x3
0 = - = =
(1 - x2)2 (1 - x2)2 (1 - x2)2 (1 - x2)2
Again, you only have to worry about when the numerator of this is zero. So all you
have to do is solve
-x4 + 3x2 = -x2(x2 - 3) = 0So to make the numerator zero, either
_
x = ±Ö3 = ±1.732050808...
If you eyeball the graph, you will be able to see this. If you knew this when you
plotted the graph, it would give you more information about the shape of the
graph, as you would have had to plot a 45 degree up-slope at both of these
x's. But know points off if you didn't do this as the original
problem didn't ask you to.
Graph the following function, identifying all zero crossings, critical points, inflection points, and horizontal and vertical assymptotes.
x
f(x) =
(1 - x)2
Step 1: Factor the denominator. This is hardly a step since it already
is factored. So just identify where the denominator is zero, which you need
to know in order to put in your vertical assymptotes. Then
Clearly the only place where the denominator is zero is at
Step 2: Identify the zero crossings. This should be a piece of cake after
the last problem.
The only place where the numerator can be zero is at
Step 3: Find the derivative of f(x). This will enable you to find the critical points. Here is the function again so you can see it as you work this step:
x
f(x) =
(1 - x)2
When you are done calculating,
You needed to use the
(1 - x)2 - x(2)(1 - x)(-1) (1 - x)( (1 - x) + 2x)
f'(x) = = =
(1 - x)4 (1 - x)4
x + 1
=
(1 - x)3
To get the middle expression from the left-hand expression, you factor a
Observe that
Step 4: Identify the critical points. You need to find where f'(x) is zero.
This one is pretty easy. When you have it,
Remember that you the only candidates for critical points are where the numerator of
f'(x) is zero. That only happens at
Step 5: Find the second derivative of f(x). This will enable you to identify any inflection points. If you make no mistakes doing this calculation, you should get a simplifying cancellation. Since you are taking the derivative of f'(x) to find the second derivative of f(x) here again is f'(x):
1 + x
f'(x) =
(1 - x)3
When you have it, Here is the second derivative done out for you:
(1 - x)3 - (1 + x)(3)(1 - x)2(-1)
f"(x) =
(1 - x)6
You should see that there is a common factor of
(1 - x) + 3x + 3 4 + 2x
f"(x) = =
(1 - x)4 (1 - x)4
Step 6: Identify any inflection points.
You do this by solving
The only candidates for inflection points are where the numerator of f"(x) is
zero. The numerator is
Step 7: Find the limits of f(x) as x goes to infinity and minus infinity.
This will tell you where any horizontal assymptotes are. Again pay attention to whether
f(x) is positive or negative as it goes to infinity and as it goes
to minus infinity. With regard to these limits, this problem is
very similar to the Graphing Problem 3.
Once again you have a denominator that grows with the square of x and a numerator that grows only linearly with x. So as the magnitude of x gets big, you expect that f(x) will get close to zero. And that's where the horizontal assymptote of this one is.
Observe also that the denominator of f(x) is always positive. This means that the sign of f(x) is entirely dependent on the numerator, which is equal to x. Hence whenever x is positive, f(x) is also positive. And likewise, whenever x is negative, f(x) is negative.
From all you have done so far you can reach certain conclusions about the trace
of this f(x). You know that
Since the critical point is a minimum, the function, f(x), must
be concave up at the critical point. To the left of the inflection point
the concavity must turn around, so expect the function to be concave
down in that region. You can test this hypothesis by putting a value
to the left of the inflection (say
To the right of the critical point you have f'(x) positive
until it gets to the vertical assymptote. So expect the trace to
head for plus infinity as it approaches that assymptote from the
left. But when
Step 8: Plot the graph. Then
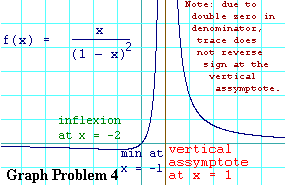
Here it is. Try doing the same thing I did last time in my final notes
to demonstrate that the only place where the trace slopes up at exactly
a 45 degree angle is at
Also recollect the cautionary note I gave you in Graphing Problem 1.
That is that the first derivative retaining its sign when x passes
through zero in the denominator is guaranteed
only if it is a single zero. Here we have a double zero in the denominator
at
Move on to 6.1 Be Fruitful and Multiply (exponentials and logs)
email me at hahn@netsrq.com