

Back in the 1960's, the banks in the United States were regulated by the federal government. One of the regulations placed a ceiling of 6% per annum on interest that they could pay depositors on passbook savings accounts. By the late 1960's economic forces were causing funds available to the banks to be in short supply. They all raised their deposit interest rates to the maximum in order to attract depositors. They also gave away toasters and radios to new depositors.
As money grew even tighter, the banks looked for loopholes in the 6% maximum regulation. And what they found was that there was no regulation on how often they could compound the interest. Traditionally they had been compounding annually. So $100 left on deposit for one year earned $6. Now they started compounding quarterly. So in effect, they were paying 1.5% per quarter. This way, $100 left on deposit for three months earned $1.50. So after three months, your account balance would be $101.50. The next three months would earn 1.5% of $101.50, or $1.52. So six months into the year, your $100 would become $103.02. From six months to nine months, you would earn interest on that amount, and end up with $104.57. And from nine months to the end of the year you would earn interest on that amount and end up with $106.14. So instead of earning just 6% per annum on your money, you were effectively earning 6.14% on your money.
Soon all the banks were offering quarterly compounding. To compete for deposits, some banks began offering monthly compounding. This is equivalent to giving you 0.5% on your money each month. And when you work it out, you end up with an effective per annum rate of 6.17%
Well, from monthly compounding it went to daily compounding. That gives you an effective rate of 6.18%. Finally a few banks offered continuous compounding. "Your money earns interest by the second," the ad copy went. So what is the effective per annum rate of compounding 6% per annum continously?
First, of course, we must come to terms with what is meant by
continuous compounding. If we are going to compound a 6% rate
n times per year, then we divide the year into n
equal intervals and pay 6/n% at the end of each interval.
That is the same as multiplying the account balance at the end
of each interval by
P = $100 × (1 + 0.06/n)n eq. 8.1-1So the effective per annum rate, r, in percent, would be
r = 100% × ( (1 + 0.06/n)n - 1) eq. 8.1-2The logical thing to do to find what happens when you compound continuously would be to see what limit the above expressions go to when n grows without limit. The crucial expression whose limit we would like to find is
y = lim (1 + 0.06/n)n eq. 8.1-3
n > ¥
Now we are stuck with the problem of taking this limit.
From what you learned in the section on
ln(y) = lim n ln(1 + 0.06/n) eq. 8.1-4a
n > ¥
If you make the substitution of
ln(1 + 0.06h)
ln(y) = lim eq. 8.1-4b
h > 0 h
Observe that as h approaches zero, Finding the limit of equation 8.1-4b is a specific case of finding the limit, in general, of
f(x)
lim eq. 8.1-5
x > c g(x)
when the limits of both f(x) and g(x) approach
zero as x approaches c.
|
As an illustration of this, let's take the example of
Now look at figure 8-1. It shows a plot of both these functions
right around the point, |
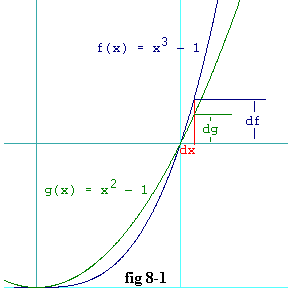 |
f(1 + dx) = df eq. 8.1-6a
and
g(1 + dx) = dg eq. 8.1-6b
Recall from our discussions of the
f(c) + h f'(c) eq. 8.1-7aAnd the smaller h is, the more accurate the approximation is. Well here you know that
f(1) + dx f'(1) = dx f'(1) eq. 8.1-7bLikewise, since it is also true that
g(1) + dx g'(1) = dx g'(1) eq. 8.1-7cSo you should be able to approximate the quotient of
dx f'(1) f'(1)Not only that, the closer to zero you make dx the better the approximation. And the limit of the approximation as dx approaches zero will be exactly equal to the quotient of f'(1) over g'(1). In this case you have=eq. 8.1-8 dx g'(1) g'(1)
x3 - 1 f'(1)
lim = = 1.5 eq. 8.1-9
x > 1 x2 - 1 g'(1)
What we have just done above is applied a powerful trick for taking
limits called L'Hopital's Rule (that's
pronounced "LOW - pea - tal". Sometimes you will see it spelled,
L'Hospital, but the pronounciation is the same). L'Hopital's Rule
says this: If f(x) and g(x) are continuous and
have derivatives that are continuous (on some open interval that
contains c), and both
f(x) f'(c)
lim
|

Figure 8-1 shows why it works. Because both f and g
are zero at
Observe that in the diagram, dx and df form two legs of a right triangle. The curve, f(x), very nearly forms the hypotenuse of that triangle. And the smaller dx is, the closer the f(x) curve becomes to being the hypotenuse. So we would expect that df can be found simply by multiplying dx times the slope of the curve -- and that slope is f'(c) (where c is the point at which f(x) crosses the x axis).
Of course you can make the identical argument for finding dg
from dx and g'(c). So as dx goes to zero,
the ratio of
Now let's return to problem of interest rates being compounded continuously. We had gotten as far as:
ln(1 + 0.06h)
ln(y) = lim eq. 8.1-4b
h > 0 h
To find this limit, you simply apply L'Hopital's rule to it. Here you
have
ln(1 + 0.06h) 0.06/(1 + 0.06h)
ln(y) = lim = lim eq. 8.1-11a
h > 0 h h > 0 1
When you take the limit as h goes to zero of the right-hand
expression, you find that ln(y) = 0.06 eq. 8.1-11bThis means that
y = e0.06 = 1.061836547... eq. 8.1-11cHow much better is that than compounding daily? This corresponds to an effective rate of 6.1836547%. Compounding daily corresponds an effective rate of 6.183131%. On a $10,000 savings account, compounding continously yields about a nickel more per year than compounding daily. Of course, over the years, those nickels add up.
Lets try another problem. We'll find
ln2(x)
lim eq. 8.1-12
x > 1 (x - 1)2
Step 1: What do the numerator and denominator go to? Since
Step 2: Take the derivatives of the numerator and denominator.
You can apply the
2 ln(x)And the derivative of the denominator is an easy application of the chain rule. For the derivative of the denominator you getx
Step 3: Apply L'Hopital's Rule. The rule says that the limit of the numerator divided by the denominator is the same as the limit of the derivative of the numerator divided by the derivative of the denominator. So you have
ln2(x) 2 ln(x)
lim = lim eq. 8.1-13
x > 1 (x - 1)2 x > 1 2x(x - 1)
Step 4: Take the limit of the new quotient.
First, cancel common the factor of 2 from the numerator and
denomonitator.
Trouble is, after you do that, the new quotient still has numerator and
denominator of zero when
Step 5: Find the derivatives of the numerator and denominator of
the new quotient.
We know that the derivative of ln(x) is 1/x. That takes
care of the numerator. The denominator,
Step 6: Apply L'Hopital's Rule for a second time. This gives you
ln(x) 1
lim = lim 8.1-14
x > 1 x(x - 1) x > 1 x(2x - 1)
Step 7: Take the limit.
The numerator of the new new quotient is 1 no matter what you
put in for x. If you put
The point of the above example is to illustrate that with L'Hopital's rule, sometimes once is not enough. If you apply it once and both the numerator and denominator are still zero, simply apply it again, as we did here. If numerator and denominator are still both zero, apply yet again. And keep doing that until you end up with a quotient that has either numerator, denominator, or both not equal to zero. If what you end up with has a nonzero denominator, then you can divide out the quotient and produce a limit. If the denominator ends up as zero but the numerator ends up nonzero, then the quotient has no limit.
1) Use L'Hopital's Rule to find the limits of the following:
a) ex - 1
lim
x > 0 x
b) ex - 1 - x
lim
x > 0 x2
c) ex - 1 - x - (1/2)x2
lim
x > 0 x3
d) ex - 1 - x - (1/2)x2 - (1/6)x3
lim
x > 0 x4
Can you discern a pattern here? If I had put up an example e),
what do you suppose it would have been? How would its limit compare
to the limits of the above examples?
2) Show how L'Hopital's Rule produces the expected result when applied to
f(x) - f(c)
lim
x > c (x - c)
Assume that f(x) is continuous and differentiable over some
open interval that includes 3) Find the limit:
arcsin(x) - p/2
lim
x > 1 Ö1 - x2
4) Find the limit of
lim x sin(1/x)
x > ¥
We already know that if you have a quotient whose numerator and denominator both go to zero in the limit, you need to analyse the problem further in order to determine the limit of the quotient. L'Hopital's Rule is a tool for doing such analysis. But it is also true that if both the numerator and denominator of a quotient grow without limit (that is they go to infinity) then you also need to further analyse the problem in order to determine the limit of the quotient.
It turns out that L'Hopital rules in this case as well. Here's why. Suppose you have two differentiable functions f(x) and g(x), both of which which increase without limit as x approaches c. They are allowed to increase in either the positive or negative direction (that is, we are allowing them to go to either plus or minus infinity as x goes to c, and we will even allow one to go to plus infinity and the other to go to minus infinity). We would like to find
f(x)
lim eq. 8.1-15a
x > c g(x)
But this is the same as
1
g(x)
lim eq. 8.1-15b
x > c 1
f(x)
Observe that both the numerator expression, 1/g(x), and
the denominator expression, 1/f(x), go to zero as x
approaches c. Why? Because both g(x) and f(x)
go to infinity (or minus infinity) as x approaches c.
And because both numerator and denominator of equation 8.1-15b go to
zero, we can apply
L'Hopital to it by taking the derivative of both
the numerator and denominator.
Since both 1/g(x) and 1/f(x) are composite functions,
we shall use the
1 g'(x)
-
f(x) g(x) g2(x)
lim = lim = lim eq. 8.1-15c
x > c g(x) x > c 1 x > c f'(x)
-
f(x) f2(x)
or, using a little algebra to simplify this, we have
f(x) f2(x)g'(x)
lim = lim eq. 8.1-15d
x > c g(x) x > c g2(x)f'(x)
Now if we divide through by f2(x) and multiply through
by g2(x), we end up with
g(x) g'(x)
lim = lim eq. 8.1-16
x > c f(x) x > c f'(x)
And if you take the reciprocal of both sides you get
f(x) f'(x)
lim = lim eq. 8.1-17
x > c g(x) x > c g'(x)
This is just L'Hopital's Rule all over again.
In other words, we have used L'Hopital's Rule for quotients whose numerator and denominator both go to zero in the limit, and we have shown that it is a necessary consequence that L'Hopital's Rule applies also to quotients whose numerator and denominator both go to infinity (or minus infinity) in the limit (you will recall that we prefaced this whole thing by with the condition that both f(x) and g(x) go to either infinity or minus infinity when x approaches c).
Here is an example. Find the limit of
ex
lim eq. 8.1-18a
x > ¥ ex + 1
Step 1: Confirm that both numerator and denominator grow without limit.
That's pretty easy. We know that ex gets very big very
fast as x increases, and there is no limit to how big it can get.
Since both numerator and denominator have an ex term
in them, clearly both numerator and denominator go to infinity as x
goes to infinity.
Step 2: Find the derivatives of numerator and denominator. Since ex is its own derivative, we have that both numerator and denominator have derivatives of ex
Step 3: Apply L'Hopital's Rule. That means that the limit of the quotient of numerator over denominator is equal to the limit of the quotient of the derivative of the numerator over the derivative of the denominator.
ex ex
lim = lim eq. 8.1-18b
x > ¥ ex + 1 x > ¥ ex
Step 4: Take the limit. Clearly the ex in the numerator of the right-hand expression cancels with the ex in the denominator. So
ex
lim = 1 eq. 8.1-18c
x > ¥ ex + 1
5) You may have heard at one time or another that 00 is undefined. All other numbers taken to the zero power, though, yield unity:
x0 = 1 for all x ¹ 0But you also have that zero raised to any positive power is zero.
0x = 0 for all x > 0If you take the limit of the first expression as x approaches zero you'd expect it to go to the same limit as when you take the limit of the second expression as x approaches zero. But this does not happen. The limit of the first is 1 while the limit of the second (as x approaches zero from above) is 0. That is why we have to leave 00 undefined. But just for fun, try using a third limit to see what possibilities there are for 00. Find the limit of
lim xx
x > 0+
Hint: Recall from your study of logs and exponentials that this is
the same as
lim ex ln(x)
x > 0+
so it is useful to find the limit as x approaches zero (from above)
of 6) Find the limit of
A0 + A1x
lim
x > ¥ B0 + B1x
Where A0, A1,
B0, and B1 are all constants,
and 7) Suppose that P(x) and Q(x) are both polynomials of the same degree, n. That is,
P(x) = A0 + A1x + A2x2 + ... + Anxnand
Q(x) = B0 + B1x + B2x2 + ... + Bnxnwhere the A's and B's are all constants, and
P(x) An
lim =
x > ¥ Q(x) Bn
for any degree, n, you might choose for both polynomials, P
and Q.
8) Find the limit of
lim x e-x
x > ¥
9) Use induction along with the result from problem 8 to show that
lim xn e-x = 0
x > ¥
for any natural number, n, no matter how large n is.

Here's an example of a problem that L'Hopital's Rule does not immediately apply to but you wish it would.
_______
lim Öx2 + 5x - x eq. 8.1-19
x > ¥
L'Hopital's Rule applies to ratios, but this is a difference. The trick here
is to use the same principles that we used to develop L'Hopital's Rule, but
apply them to this difference. In the development of L'Hopital's Rule we
approximated f(x+h), where f(x + h) » f(x) + h f'(x)where the symbol, », means "is approximately equal to." Likewise by subtracting f(x) from both sides
f(x + h) - f(x) » h f'(x)The only thing special about L'Hopital's use of this is that he looked at the case where
We know that the approximation gets better and better as h goes to zero. But suppose that instead of letting h go to zero, you keep h the same and let x go to infinity instead. As x gets big, h is a tinier and tinier fraction of x. And the approximation above might still apply. That is it will apply if a certain limit does indeed exist, namely
lim h f'(x) = lim f(x + h) - f(x) eq. 8.1-20
x > ¥ x > ¥
If the limit on the left exists, it will be equal to the limit
on the right.
I know that this sounds a little complicated, but think of it this way. Suppose you had a car whose maximum speed was 50 meters per second. It never actually reaches that speed. But if you take it onto the highway and floor it, 50 meters per second is the limit of how fast it goes. Every minute you keep it floored, the car's speed gets closer to 50 meters per second, and if you floor it long enough it will get as close to 50 meters per second as you like.
Now think about the distance between where the car is at any moment and where it will be 2 seconds hence. That distance also has a limit. And that limit is 2 seconds times 50 meters per second, which is 100 meters. It only makes sense.
That is all that equation 8.1-20 is saying. With the car, f(t) is the car's position at any time. f'(t) is the car's speed. h is the 2 seconds. Think about this until you understand it.
Now we turn it up a notch. Suppose you have a composite:
f( g(x) + h(x) )Let's suppose that g(x) and h(x) both go to infinity as x goes to infinity. Further suppose that
h(x)
lim = 0 eq. 8.1-21
x > ¥ g(x)
So, if you have all these conditions, then what is the limit of
lim f(g(x) + h(x)) - f(g(x)) eq. 8.1-22
x > ¥
You apply the same principle, but in equation 8.1-21 you replace x
with g(x) and replace h with h(x).
lim f(g(x) + h(x)) - f(g(x)) = lim h(x) f'(g(x)) eq. 8.1-23
x > ¥ x > ¥
Here is equation 8.1-19 again:
_______
lim Öx2 + 5x - x eq. 8.1-19
x > ¥
Observe that for positive x
__
x = Öx2
so equation 8.1-19 is really
_______ __
lim Öx2 + 5x - Öx2 eq. 8.1-19a
x > ¥
Note also that
5x
lim = 0 eq. 8.1-19c
x > ¥ x2
If f() is taking the square root,
1 1
f'(g(x)) = = eq. 8.1-24a
2Öx2 2x
h(x) 5x 5
lim h(x) f'(g(x)) = lim = = eq. 8.1-24b
x > ¥ x > ¥ 2x 2x 2
You could have solved this same problem using L'Hopital's rule, but the path
is not as direct (using L'Hopital in this case is doing it the hard way.
But I'll do it out that way just to show that you end up with the same answer).
You have to do some algebraic look-ahead first -- that
is you would have to see that it was prudent apply the
_______
Öx2 + 5x + x
Öx2 + 5x + x
which, of course, is equal to one and doesn't change anything:
_______ x2 + 5x - x2 5x
lim Ö x2 + 5x - x = lim = lim
x > ¥ x > ¥ Öx2 + 5x + x x > ¥ Öx2 + 5x + x
eq. 8.1-25
You can apply L'Hopital's rule by taking the derivatives of
the numerator and denominator to this and you get
5
lim eq. 8.1-26
x > ¥ 2x + 5
+ 1
2Öx2 + 5x
which would be fine if it weren't for that nasty fraction on the left
side of the denominator. In order to take this limit you have to find
out what the limit of the nasty thing is, so you have to apply L'Hopital's
rule to it separately. Suppose the limit of the nasty thing is L.
Then
______
2x + 5 2 2Öx2 + 5
L = lim = lim = lim
x > ¥ 2Öx2 + 5x x > ¥ 4x + 10 x > ¥ 2x + 5
2Öx2 + 5
eq. 8.1-27
The middle expression in the above equation is the left-hand expression
after L'Hopital has been applied. The right-hand expression is a simplification
of the middle expression.
What you learn from this exercise is that if L is the limit
of equation 8.1-27, then
5 5
lim = eq. 8.1-28
x > ¥ 1 + 1 2
This is the same answer we got doing it using the approximate-form method,
but what a lot more work (not to mention a lot more opportunities to
make a mistake). The further advantage of the approximate-form method
is that it can do differences that this other method can't.
lim (x3 + 5x2)1/3 - x eq. 8.1-29
x > ¥
The difference of squares won't help you whip this one into shape
for applying L'Hopital. But in the approximate form method, you have
f() as taking something to the 1/3 power. You have
1
f'(g) = g-2/3 eq. 8.1-30a
3
1 1
f'(g(x)) = (x3)-2/3 = eq. 8.1-30b
3 3x2
Now you can apply the approximate form:
5x2 5
lim (x3 + 5x2)1/3 - x = lim x + - x = eq. 8.1-31
x > ¥ x > ¥ 3x2 3
Move on to The Dance of the Derivatives (Related Rates)
email me at hahn@netsrq.com