In all likelihood, you have already studied logarithms when you took algebra. At that time, they probably seemed useful only for carrying out difficult computations back in the days before electronic computers. But in the ediface of calculus, logarithms in general, and the natural log function in particular, are a keystone in our understanding. Because they are so essential to calculus, they turn up everywhere in physics, chemistry, and engineering. Even with modern computers to help us calculate, we still wouldn't get very far without logarithms.
In the last section we defined the natural log function, ln(x), as
xh - 1
ln(x) = lim eq. 6.3-1
h > 0 h
where
That definition of the natural log function arose because of
the role it plays in
finding the derivative of
ln(ab) = ln(a) + ln(b) eq. 6.3-2a
and
ln(bn) = n ln(b) eq. 6.3-2b
And you would expect it to obey those rules -- otherwise naming it
the natural log would have been inappropriate, wouldn't it?
These very properties, though, can be deduced from the limit definition
alone. Those derivations are given here as a
When they introduced you to logarithms in algebra, they probably talked about the base of a logarithm. Usually you study logs base 10 before any others. And the symbol for the log base 10 of x was log10(x). Recall now that for log10 you had
.
.
.
log10(0.0001) = -4
log10(0.001) = -3
log10(0.01) = -2
log10(0.1) = -1
log10(1) = 0
log10(10) = 1
log10(100) = 2
log10(1000) = 3
log10(1000) = 4
.
.
.
table 6.3-1
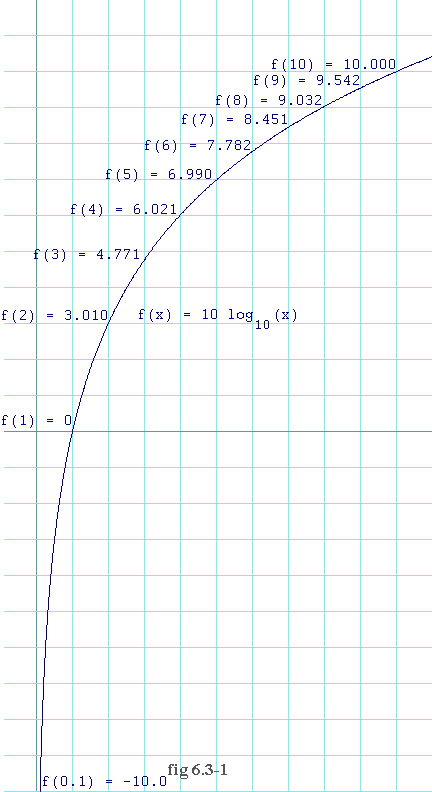
Figure 6.3-1 shows a plot of
Logs base 10 obey the same product rule as natural logs. That is
You probably also learned that
log10( 10x ) = xand
10log10(x) = xNow that you know that exponentials are always continuous functions, and that they are monotone (that is either always increasing or always decreasing), You can use
x = 10yyou could find a yhigh such that
x < 10yhighby choosing yhigh big enough and a ylow such that
x > 10ylowby choosing ylow small enough. Since 10y is a continuous function of y, the intermediate value theorem demands the existence of a y that makes
You can also readily show that log10(x) is monotone
increasing. It follows from 10x being monotone
increasing. If log10(x) were not monotone increasing,
then their would be some
I have a diversionary page that will bring back into focus what logs base
10 are all about. It is optional material, and you can
get to it by
And what about logs using bases other than 10? Suppose you wanted log base 7 of x. Observe that
x = 7log7(x) eq. 6.3-3awhich follows from log and exponentiation being inverses of each other. If you take the log base 10 of both sides and apply what we know about logs, you have
log10(x) = log7(x) × log10(7) eq. 6.3-3bDivide out log10(7) and you have
log10(x)
log7(x) = eq. 6.3-3c
log10(7)
And in general, if you have log to the base a of x, you
can convert it to log to the base b of x by this formula:
loga(x)
logb(x) = eq. 6.3-4
loga(b)
where a, b, and x can be any positive real numbers.
Here is one more property of logs that is important. If you take the log to the base b, where b is any positive real number, then
logb(b) = 1 eq. 6.3-5You should be able to verify this yourself by raising b to the power on each side of equation 6.3-5 and remembering that logs and exponentials are inverses of each other.
This has all been review of material you had in algebra so far. Now let's get down to what logs in general and natural log in particular have to do with calculus. Remember that we defined the following limit as natural log:
xh - 1
ln(x) = lim eq. 6.3-6
h > 0 h
If the function, ln(x), is truly a log in the sense that log to
the base 10 and log to the base 7 are logs, then
ln(x) must have a base as well. That means that there must be
a positive real number, e, such that for all positive
x it is true that
ln(x) = loge(x) eq. 6.3-7And from equation 6.3-5, we also have
eh - 1
ln(e) = lim = loge(e) = 1 eq. 6.3-8
h > 0 h
It turns out that the real number that satisfies this equation is irrational.
To 16 places,
(ex)h - 1 ehx - 1
ln(ex) = lim = lim eq. 6.3-9a
h > 0 h h > 0 h
Now we employ a trick we've used before. We substitute k for
hx. If h goes to zero, then k certainly must
go to zero also. After all, we have
ek - 1
ln(ex) = lim x eq. 6.3-9b
k > 0 k
But we already know that
ek - 1
lim = 1 eq. 6.3-9c
k > 0 k
That is because we defined e to be the real number that solves this
equation. So we are left with
ln(ex) = lim x × 1 = x eq. 6.3-9d
k > 0
which finishes the proof and confirms that ln(x) and
ex are inverses of each other. It also shows
that natural log of x is the same thing as log to the base
e of x.
Now if
f'(x) = ln(e) × ex = ex eq. 6.3-10That's right. The function
bx = ex ln(b) eq. 6.3-11
which holds for any positive real number, b, and any real number,
x. You should be able to verify this identity for yourself based
upon the discussion so far. If you can't, you should go back and review
until you can.
A few other things you should know about ex. Like
other exponential functions, it is defined and continuous for all real
x. And like other exponential functions, the value of
ex is positive for all real x.
Just to emphasize that last remark, if x is any real number,
ex is never zero and never negative.
Another useful fact is that
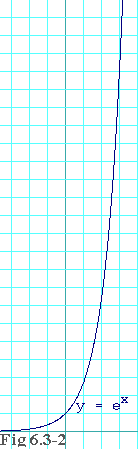
Figure 6.3-2 shows a plot of ex. Observe that
this function always returns a result that is positive. Like other
exponential functions, it crosses the y-axis at
The function,
We'll do the easy one first. We know from the discussion so far that
ln(x) and ex are inverses of each other.
That means that if
ef(x) = eln(x) = x eq. 6.3-12Now remember that ex is its own derivative. Using the
ef(x) f'(x) = 1 eq. 6.3-13aBut from eq. 6.3-12, we know that
x f'(x) = 1 eq. 6.3-13bor equivalently
1
f'(x) = eq. 6.3-13c
x
And that's the derivative of the natural log function -- 1/x.
Remember it. It comes up all the time.
But your instructor might ask you to find the derivative of the natural log using limits. Recall that the derivative of a function, f(x), was defined back in unit 4 as
f(x + h) - f(x)
f'(x) = lim eq. 6.3-14
h > 0 h
And you have the limit definition of ln(x). Putting this all
together, you get that if
ln(x + h) - ln(x)
f'(x) = lim eq. 6.3-15a
h > 0 h
Now substituting the limit definition for ln(x) (and
using k instead of h for the limit variable in
that definition) we have:
(x + h)k - 1 xk - 1
-
k k
f'(x) = lim eq. 6.3-15b
h > 0 h
k > 0
Here we are taking the limit as two variables, h and k,
both go to zero.
This looks pretty nasty, but after a little algebra and some cancellation
you have
1 (x + h)k - xk
f'(x) = lim - eq. 6.3-15c
h > 0 k h
k > 0
Now look at the right hand factor of the product in eq. 6.3-15b. Isn't
that just the limit formula for the derivative of xk?
And isn't the derivative of xk equal to
1
f'(x) = lim - kxk-1 eq. 6.3-15d
k > 0 k
Clearly the k and the 1/k cancel each other. We're left
with
f'(x) = lim xk-1 eq. 6.3-15e
k > 0
Well that's an easy limit to take. We know exponentials are continuous,
so as k goes to zero, k-1 goes to -1 and
xk-1 goes to x-1. That gives
1
f'(x) = x-1 = eq. 6.3-16
x
So there it is, proved two different ways. The derivative of ln(x)
is 1/x. And it is this property of the natural log that makes it
show up so often in calculus and physics.
1) You already should know that
2) Take the derivatives of the following two expressions using
the
f(x) = ln(1 + x) + ln(1 - x)and
f(x) = ln(1 - x2)Note that you can easily show using factoring and log identities that these two expressions are equal before you take the derivative. But see if you can take the derivative of the second without factoring the polynomial inside the log. This will exercise your skills at applying the rules for taking derivatives. Work it out and then
3) There are some functions used in advanced calculus that grow so large so fast that it is often more convenient to deal with the natural log of such functions. If f(x) is any function whose derivative you know, write an expression in terms of f(x) and f'(x) that gives the derivative of ln(f(x)). Then Click here to see the solution.
4) The function,
5) A sample of radioactive material has
6) Find the derivative of
7) Chemists say that when a chemical system has reached a point where no further spontaneous changes are possible, it is in equilibrium. If you had, for example, a system where compound A changes into compound B, equilibrium occurs when the rate of change from A to B exactly equals the rate of change from B back to A. The system therefore is in balance.
You can find the equilibrium point of a chemical system by maximizing a quantity called entropy. The symbol commonly used for entropy is S. For chemicals in a solution, there are several variables that go into computing entropy. These are the concentration of each compound, ck, in moles per liter, the temperature above absolute zero, T, and the amount of heat energy, H, given off by the changing of one compound to another.
If the concentration of compound A is cA, then its contribution to the entropy of the system is
-R cA ln(cA)where R is a universal physical constant.
If H is the amount of heat given off by the reaction, its contribution to entropy is
H
T
Total entropy is the sum of all the contributing terms. If you
have a mole of compound A changing to a mole of compound B, for each
each mole that changes from A to B you get U units of heat.
Supposing we started with 1 mole per liter of A and none of B,
then, as the reaction progressed, the entropy per liter would be
UcB
S = -R cA ln(cA) - R cB ln(cB) +
T
Assume that temperature, T, is constant. Assume that U
is constant as well.
Observe that in this example, the sum of
cA = 1 mole/liter - cBGo ahead and eliminate cA from the entropy equation by substituting it with the right hand side of this equation. Entropy will be maximum when the derivative of S with respect to cB is zero:
dSFind that derivative and set it zero. Then substitute back to find what ratio of cB:cA produces this condition. That is the equilibrium point.= 0 dcB
You will need to use both the
This is a word problem with a lot of information in it, but you can
solve it using the material we have covered in this section.
Read it
over several times and take it a little at a time. If you have studied
chemistry, you will see a familiar formula emerge out of this. Get as
far as you can before
8) Coached Exercise
Demonstrate using limits and algebra only that the familiar identity
Move on to May the Circle be Unbroken (trig functions)
email me at hahn@netsrq.com